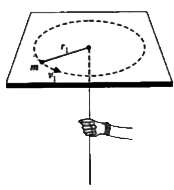
Figure shows a mass m placed on a frictionless horizontal table and attached toa string passing through a mall hole in the surface. Initially, themas movesin a circle of radius r0 with a speed v0 and the ree end of the string is held by a person. The person pulls on the string slowly to decrease the radius of th circle of r. a. Find the tension in the string when the mass moves in the circle of radius r. b. Calculate the chasnge in the kinetic energy of the mass
To solve the problem step by step, we will address both parts of the question: finding the tension in the string when the mass moves in a circle of radius r and calculating the change in kinetic energy of the mass.
1. Understanding the System:
- A mass m is moving in a circle of radius r with speed v.
- The tension T in the string provides the necessary centripetal force to keep the mass moving in a circle.
2. Centripetal Force Equation:
- The centripetal force required to keep the mass moving in a circle is given by:
Fc=mv2r
- Here, Fc is provided by the tension in the string, so we can write:
T=mv2r
3. Relating v and v0:
- Since angular momentum is conserved, we can relate the initial and final states:
Li=Lf⟹mv0r0=mvr
- Simplifying gives:
v=r0rv0
4. Substituting v into the Tension Equation:
- Substitute v into the tension equation:
T=m(r0rv0)2r
- Simplifying this gives:
T=mr20v20r3
Part B: Calculating the Change in Kinetic Energy
1. Initial Kinetic Energy:
- The initial kinetic energy Ki when the radius is r0 is:
Ki=12mv20
2. Final Kinetic Energy:
- The final kinetic energy Kf when the radius is r is:
Kf=12mv2
- Substitute v from our earlier relation:
Kf=12m(r0rv0)2=12mr20v20r2
3. Change in Kinetic Energy:
- The change in kinetic energy ΔK is given by:
ΔK=Kf−Ki
- Substituting the expressions for Kf and Ki:
ΔK=12mr20v20r2−12mv20
- Factoring out 12mv20:
ΔK=12mv20(r20r2−1)
Final Answers
- Tension in the string:
T=mr20v20r3
- Change in kinetic energy:
ΔK=12mv20(r20r2−1)
- A mass m is moving in a circle of radius r with speed v.
- The tension T in the string provides the necessary centripetal force to keep the mass moving in a circle.
- The centripetal force required to keep the mass moving in a circle is given by:
Fc=mv2r
- Here, Fc is provided by the tension in the string, so we can write:
T=mv2r
- Since angular momentum is conserved, we can relate the initial and final states:
Li=Lf⟹mv0r0=mvr
- Simplifying gives:
v=r0rv0
- Substitute v into the tension equation:
T=m(r0rv0)2r
- Simplifying this gives:
T=mr20v20r3
- The initial kinetic energy Ki when the radius is r0 is:
Ki=12mv20
- The final kinetic energy Kf when the radius is r is:
Kf=12mv2
- Substitute v from our earlier relation:
Kf=12m(r0rv0)2=12mr20v20r2
- The change in kinetic energy ΔK is given by:
ΔK=Kf−Ki
- Substituting the expressions for Kf and Ki:
ΔK=12mr20v20r2−12mv20
- Factoring out 12mv20:
ΔK=12mv20(r20r2−1)
T=mr20v20r3
ΔK=12mv20(r20r2−1)
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -1
26 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -2
14 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer
13 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
Similar Questions
A mass m is attached to a string passing through a small hole in a frictionless, horizontal surface. The mass is initially orbiting with a velocity v1 in a circle of radius r1 The string is then slowly pulled from below, decreasing the radius of the circles to r2 (i) What is the speed of the mass when the radius is r2 ? (ii) What is the tension in the string ? (iii) What is the work done in moving the mass m from r1 to r2?
View SolutionOn the surface of a solid cylinder of mass 2 kg and radius 25 cm a string is wound several times and the end of the string is held stationary while the cylinder is released from rest. What is the acceleration of the cylinder and the tension in the string ?
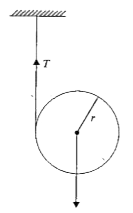
View SolutionThe mass of the part of the string below A in figure is m. Find the tension of the string at the lower end and at A.
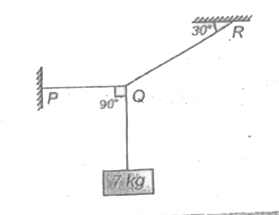
View SolutionFind the tension in the horizontal string PQ and the string QR in the given figure [ Take g =10m/s2]

View SolutionFind the tension in the horizontal string PQ and the string QR in the given figure. [Take g=10m/s2]
View SolutionAn air puck of mass m1 is tied to a string allowed to revolved in a circle of radius R on a frictionless horizontal table . The other end of the string passes through a small hole in the centre of the table , and a load of mass m2 is tied to the string? The suspended load remains in equilibrium while the pack on the tabletop revolves.

a. Find the tension in the string
b. Find the radial force acting on the puck
c. Find the speed of the puck
d. Qualitaively describe what will happen in the motion of the puck if the value of m2 is somewhat increased by placing an additional load on it.
e.Qualitaively describe what will happen in the motion of the puck if the value of m2 is instead decreased removing a part from the hanging load.
View SolutionA string of 7m length has a mass of 0.035kg. If tension in the string is 60.N, then speed of a wave on the string is
View SolutionA 5.5 m length of string has a mass of 0.035 kg. If the tension in the string is 77 N the speed of a wave on the string is
View SolutionThe string of a pendulum is horizontal. The mass of the bob is m. Now the string is released. The tension in the string in the lowest position is -
View SolutionA body of mass m is suspended by two strings making angles αandβ with the horizontal. Find the tensions in the strings.
View Solution
