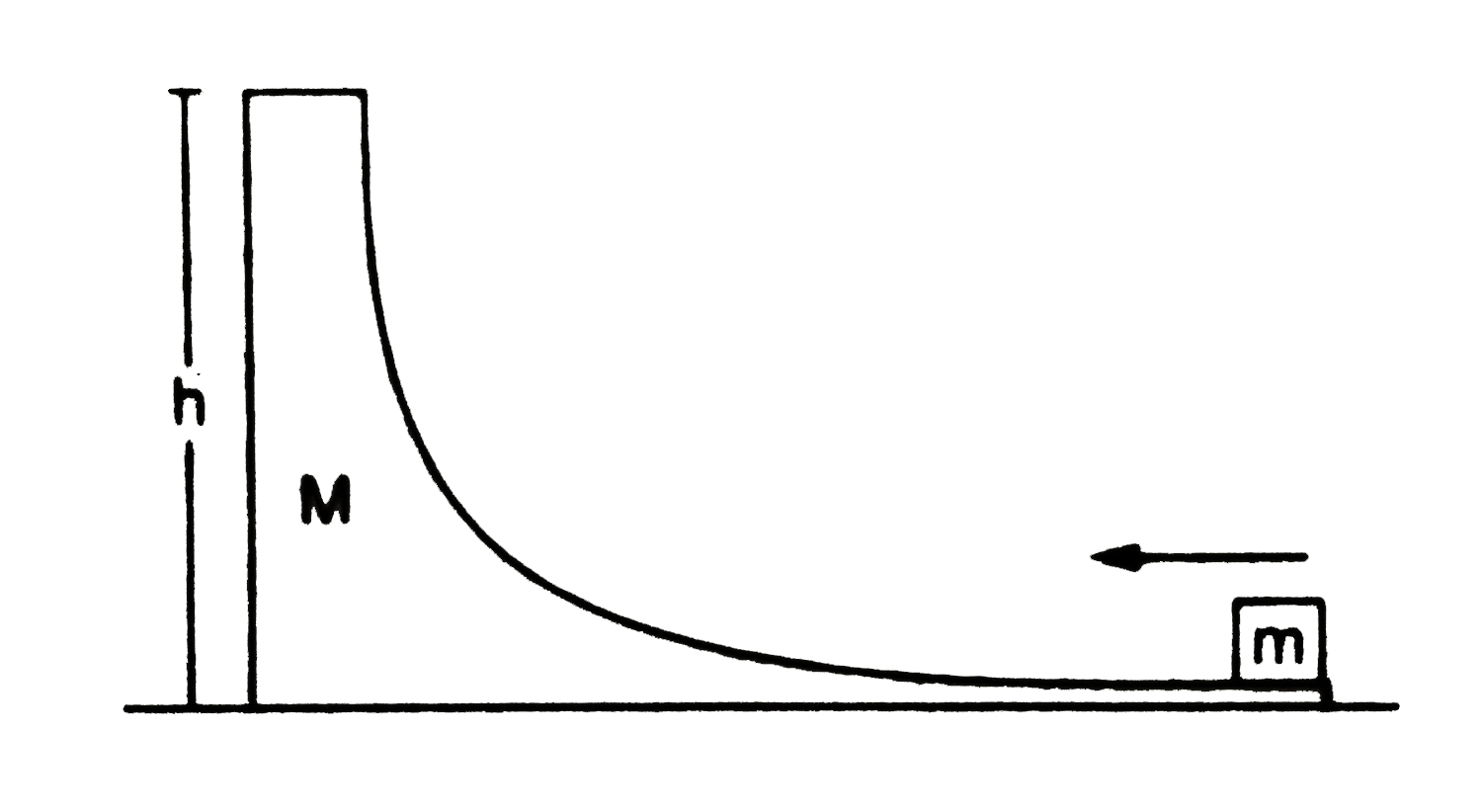
Figure shows a small body of mass m placed over a larger mass M whose surface is horizontal near the smaller mass and gradually curves to become verticle. The smaller mass is pushed on the longer on at a speed v and the system is left to itself. Assume thast all the surfaces are frictionless. a. find teh speed of the larger block when the smaller block is sliding on the vertical part. b. find the speed of the smaller mass when it breaks off the larger mas at height h. c. find the maximum height (from the ground) that the smaller mass seconds. d show that the smaller mass will again land on the bigger one. Find the distane traversed by the bigger block during the time when the smaller block was in its flight under gravity.
The correct Answer is:A, B, C, D
The mass m is given a velocity v over the larger mass M.
a. when the smaller block is travelling on the vertical part let the velocilty of the bigger block be v1 towards left
From law of conservation of momentum (in the horizontal direction)
mv=(M+m)v1
→v1=mvM+m
b. When the smaller block breaks off let its result velocity is v2
From law a conservation of energy
(12)mv2=(12)Mv21+(12)mv22+mgh
→v22=v2−Mmv21−2gh......i
→v22=v62[1−Mm,m2(M+m)2]−2gh
→v2=[(m2+Mm+m2)(M+m)2]−2gh]120
c. now the vertical component of the velocity v2 of mass m is given by
v_y^2=v_2^I2-v_1^2<br>=((M^2+Mm+m^2)/(M+m)v^2-2gh-(m^2v^2)/((M+m)^2)<br>[:. v_1=(mv)/(M+m)]<br>rarr v_y^2=(M^2+Mm+m^2-m^2)/(M+m) v^2-gh<br>rarr v_y^2=(Mv^2)/((M+m))-2gh.........ii<br>→f∈dthemaxiμmheightomthegroudn,<br>Letusas∑ethebodyrise→aheighthoveraddaboveh<br>now, (1/2)mv_y^2=mgh_1<br>rarr h_1=v_y^2/(2g).........iii<br>so→talheight=h+h_1<br>=h+v_y^2/(2g)<br>=h+(Mv^2)/((M+m)2g)-h.....iii<br>[omequationiiandiii]<br>rarr H=(Mv^2)/(2g(M+m))<br>d.∵thesmal≤rmasshasalsogotahorizontalcompo≠tnofvelocityVatthetimeitbreaksoffomM(whichhasavelocityv_1)theblockmwillaga∈landontheblockM(big≥ro≠)<br>Letusf∈doutthetimeofflightofblockmafteritbreaksoff.<br>Dur∈gtheupwardmotion(BC)<br>0=v_y-gt<br>rarr g_1=v/g<br>=1/g[(Mv^2)/((M+m)-2gh]..........iv<br>[omequationii]<br>Sothetimeforwhichthesmal≤rblockwas∈flightisgivenby<br>T=2t_1<br>=2/g[(Mv^2-2(M+m)gh)/(M+m)]<br>sothedistancetrvel≤dbythebig≥rblockdur∈gthistimeis<br>S=v_1T<br>>=(mv)/(M+m) 2/g xx[(Mv^2-(M+m)gh)]^(1/2)/((M+m)^(1/2)<br>so S=(2gv[Mv^2-2(M+m)gh)]^(1/2)/(g(M+m)^(3/2))
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Question For short Answer
25 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -2
11 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -1
18 Videos
- CALORIMETRYBOOK - HC VERMA ENGLISHCHAPTER - CALORIMETRYEXERCISE - Short answer
9 Videos
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Question for short Answer
10 Videos
Similar Questions
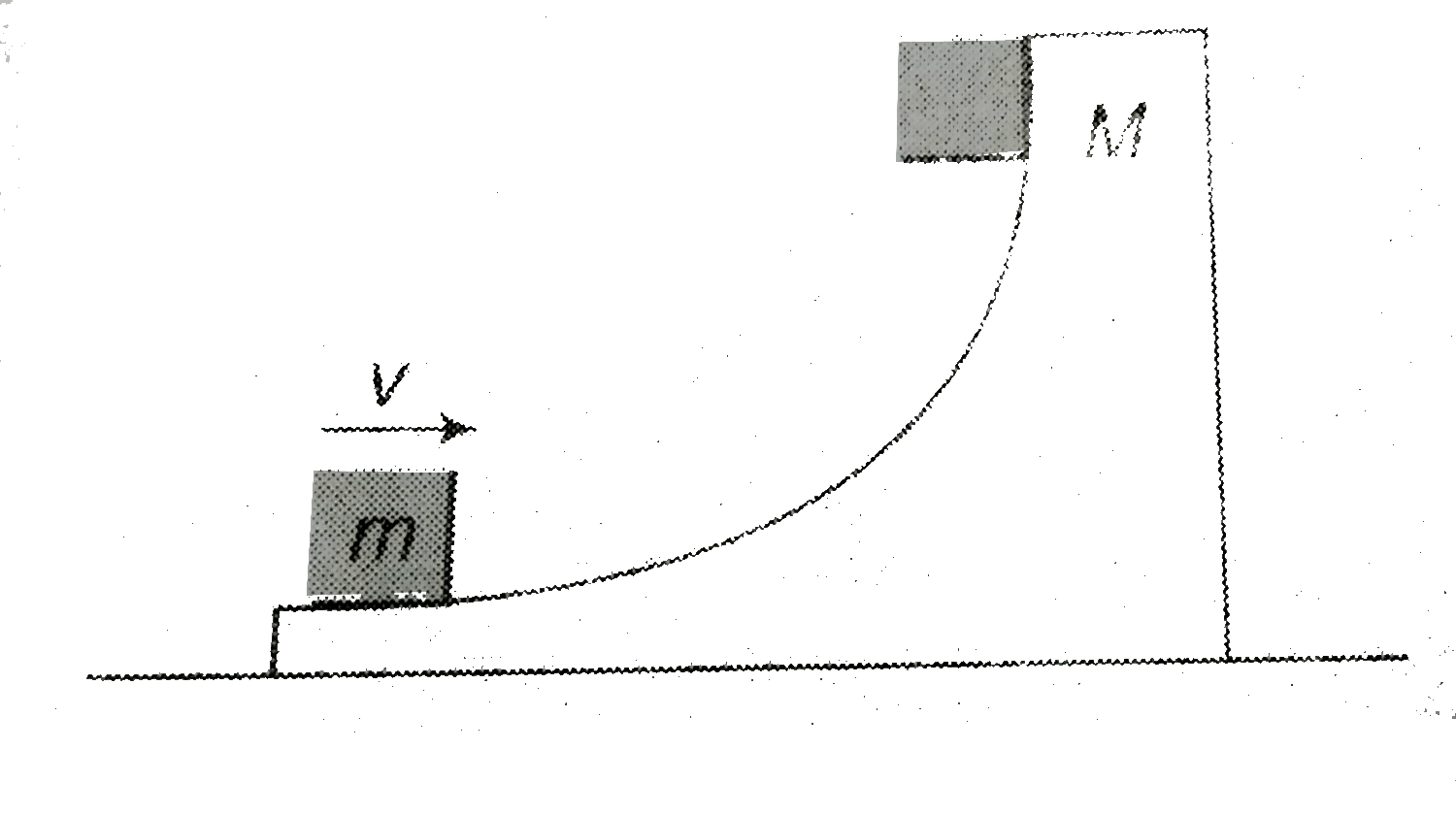
As shown , a small body of mass 50g placed over a larger mass 1950g whosw surface is horizontal near the smaller mass and gradually curves to become vertical. The smaller mass is pushed on the longer one at a speed 20m/s and the system is left to itself. All surfaces are smooth. Find the speed of the larger block when the smaller block is moving on the vertical part.
View SolutionAssuming all the surfaces to be smooth, find the acceleration of the triangular block of mass M when the block of mass m slides on it.

View SolutionFigure shows a small block of mass m which is started with a speed v on the horizontal part of the bigger block of mas m placed on a horizontal floor. The curved part of the surface shown is semicircular. All the surfaces are frictionless. Find the speed of the bigger block when the smaller block reaches the point A of the surface.

View SolutionFigure shows a small block of mass m which is started with a speed v on the horizontal part of the bigger block of mas m placed on a horizontal floor. The curved part of the surface shown is semicircular. All the surfaces are frictionless. Find the speed of the bigger block when the smaller block reaches the point A of the surface.

View SolutionA block of mass M is placed on the top of a bigger block of mass 10 M as shown in figure. All the surfaces are frictionless. The system is released from rest, then the distance moved by the bigger block at the instant the smaller block reaches the ground :
View SolutionIn figure m1=1kg and m2=4kg Find the mass m of the hanging block which will prevent the smaller block from slipping over the triangular block .All the surface are frictionless and the string and the pulleys are light

View SolutionFind the mass M of the hanging block in figure which will prevent the smaller block from sliping over the triangular blcok. All the surfaces are frictions and the strings and the pulleys are light.
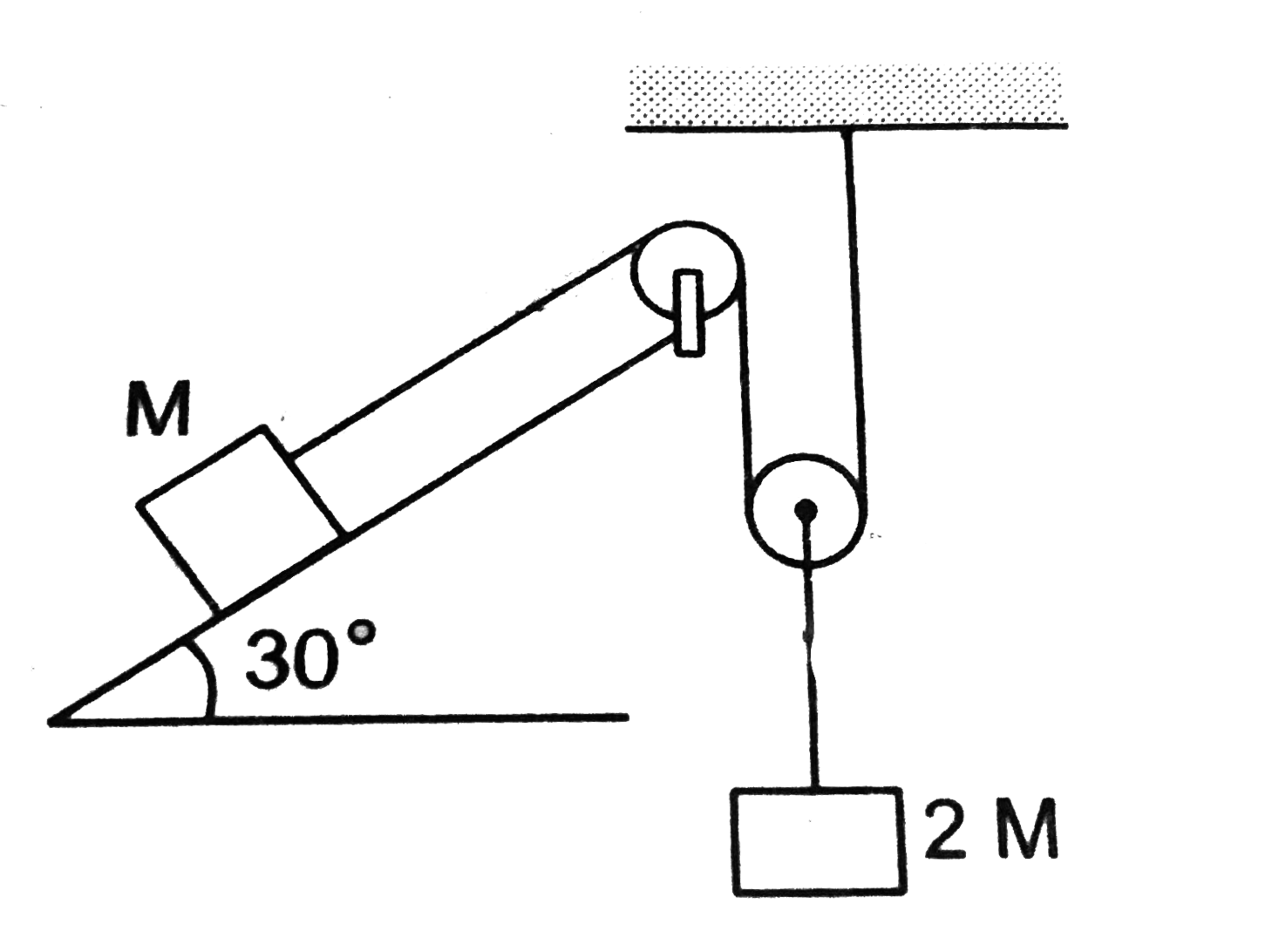
View SolutionConsider the situation as shown in the figure. All the surface are smooth and the string and pulley are light. Find the mass of the hanging block which will prevent the smaller block form slipping over the triangular block.

View SolutionConsider the situation as shown in the figure. All the surface are smooth and the string and pulley are light. Find the mass of the hanging block which will prevent the smaller block form slipping over the triangular block.

View SolutionA block of mass M is placed on the top of a bigger block of mass 10 M as shown in figure. All the surfaces are frictionless. The system is released from rest, then the distance moved by the bigger block at the instant the smaller block reaches the ground :

View Solution
