Figures 14.25 correspond to two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution (i.e. clockwise or anti-clockwise) are indicated on each figure.
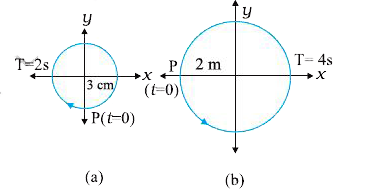
Obtain the corresponding simple harmonic motions of the x-projection of the radius vector of the revolving particle P, in each case.Solution in Gujrati
(a) Motion is in clockwise direction and at t=0, particle is at P and hence initial phase ϕ=+π2rad
∴ω=2πT=2π2 [∴T=2s given ]
∴ω=πrads−1
Equation of SHM for x-component of particle P, x=Acos(ωt+ϕ)
∴x=3cos(πt+π2)
∴x=−3sinπt cm [∴cos(π2+θ)=−sinθ].
(b) Here T= 4s and A= 2 m and initial phase ϕ=πrad
∴ω=2πT=2π4=π2rads−1
The equation of SHM for the x-component of particle P,
x=Acos(ωt+ϕ)
∴x=2cos(π2t+π)
∴x=−2cos(π2t) cm [∴cos(π+θ)=−cosθ).
Topper's Solved these Questions
- OSCILLATIONSBOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-B (ADDITIONAL EXERCISE)
9 Videos
- OSCILLATIONSBOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-B (NUMERICAL FROM DARPAN BASED ON TEXTBOOK)
15 Videos
- OSCILLATIONSBOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-B (NUMERICAL FROM TEXTUAL ILLUSTRATIONS)
40 Videos
- OBJECTIVE QUESTIONS AS PER NEW PAPER STYLE BOOK - KUMAR PRAKASHANCHAPTER - OBJECTIVE QUESTIONS AS PER NEW PAPER STYLE EXERCISE - CHAPTER - 8 (Match Type questions)
5 Videos
- PHYSICAL WORLDBOOK - KUMAR PRAKASHANCHAPTER - PHYSICAL WORLDEXERCISE - SECTION-E (QUESTIONS FROM MODULE)
9 Videos
Similar Questions
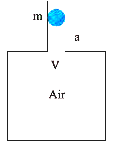
An air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].
View SolutionThe displacement of a simple harmonic oscillator is given by y=0.40sin(440t+0.61). For this, what are the value of amplitude.
View SolutionOn an average, a human heart is found to beat 75 times in a minute. Calculate its frequency and period.
View SolutionType of satellites are given in Column-I and their uses are given in Column-II. Match them properly :
Column-IColumn-II(1) Polar satellite(a) Tele communication(2) Geo-stationary satellite(b) Investigation(c) For information about atmosphere
View Solution.…. state of substance at very high temperature has generated hope of energy source for mankind.
View Solutiondepict two circulat mothions. The radius of the circle, the period of revolution, the initial position and sense of revolution are indicated in the figures. Obtain the simple harmonic motinosof the x-projection of the radius vector of the rotating particle P in each case.
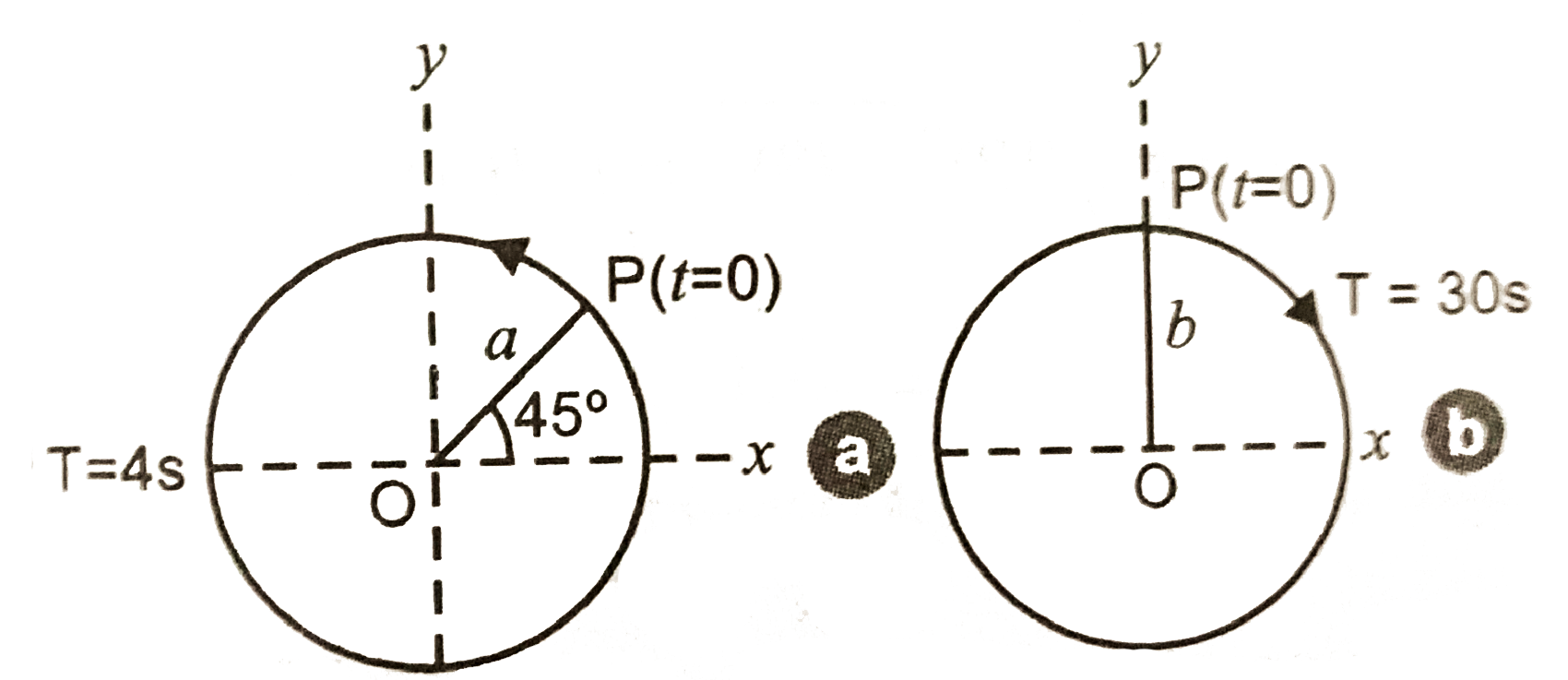
View SolutionFigures,. Correspond to two circular motions. The radius of the circle, the peirod of revolution, the initial position, and the sense of revolution (i.e. clockwise or anticlockwise) are indicated on each. Obtain the corresponding equations of simple harmonic motions of the revolving particle P in each case.
View Solutionthe circular motion of a particle. The radius of the circle, the period, sense of revolution and the initial position are indicated on the figure. The simple harmonic motion of the x-projection of the radius vector of the rotating particle P is
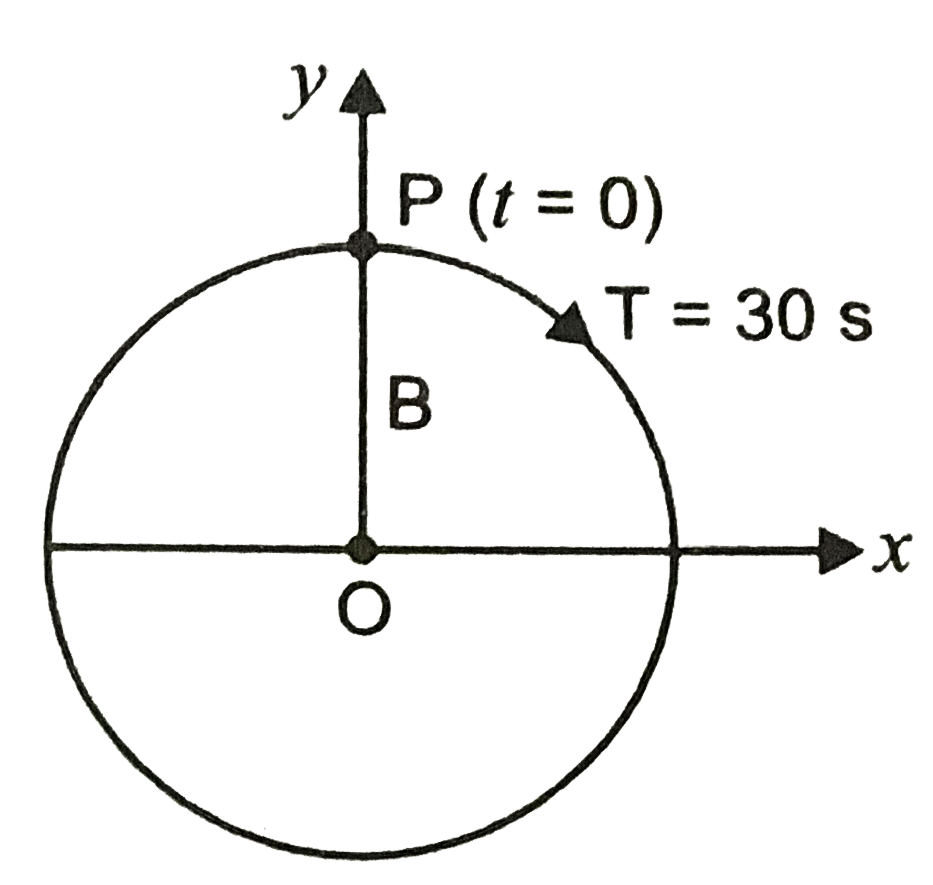
View Solution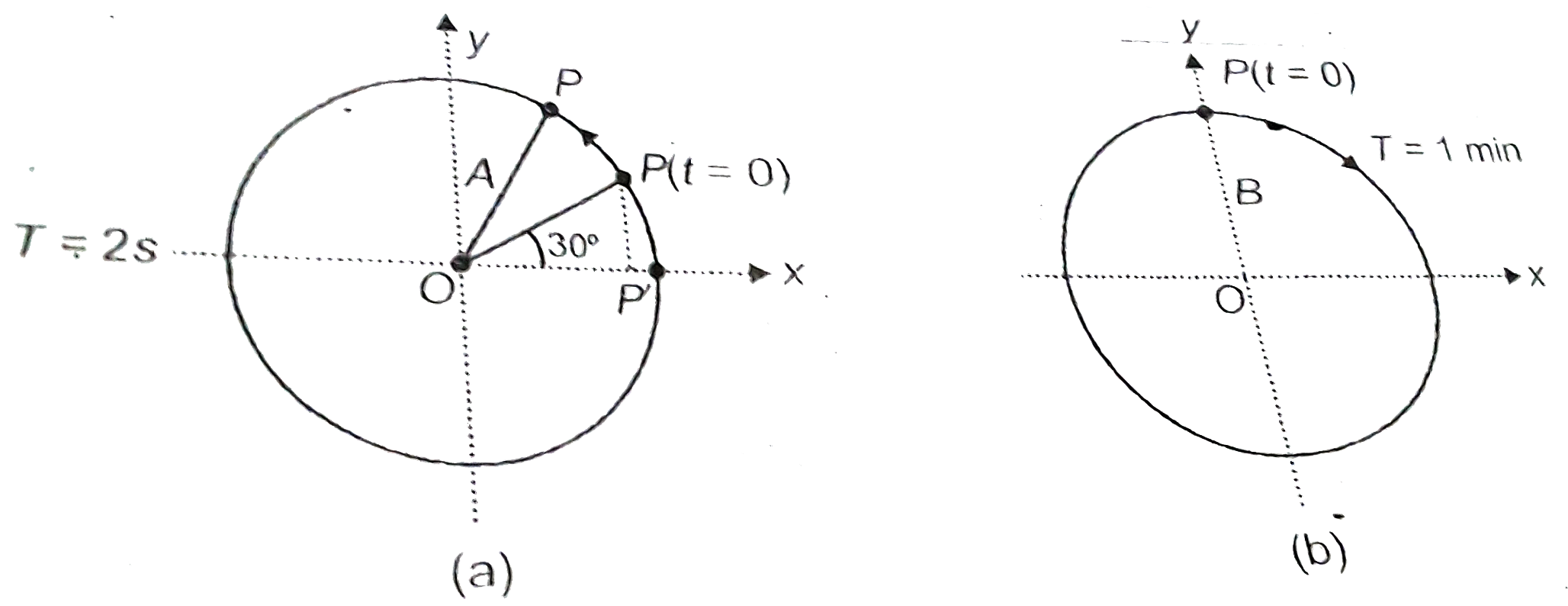
Figure depicts two circular motions. The radius of the circle, the period of revolution, the initial position and the sense of revolution are indicated on the figure. Obtain the SHMs of the x-projection of the radius vector of the rotating particle P in each case.
View SolutionFigure shows the circular motion of a particle. The radius of the circle, the period, sense of revolution and the initial position are indicated in the · figure. The simple harmonic motion of the X-projection of the radius vector of the rotating particle Pis
View SolutionFigure below correspond to two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution (i.e. clockwise or anticlockwise) are indicated on each figure. Obtain the corresponding simple harmonic motions of the x-projection of the radius vector of the revolving particle P in each case.
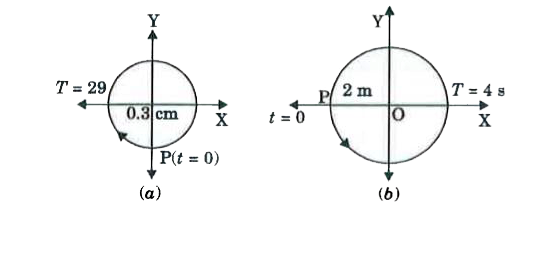
View SolutionThe figure given below depicts two circular motions. The radius of the circle, the period of revolution, the initial position and the sense of revolution are indicated in the figures. Obtain the simple harmonic motions of the x-projection of the radius vector of the rotating particle P in each case.
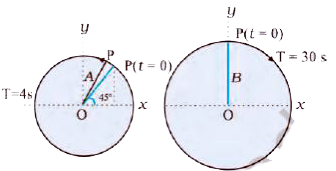
View SolutionFigures 14.25 correspond to two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution (i.e. clockwise or anti-clockwise) are indicated on each figure.

Obtain the corresponding simple harmonic motions of the x-projection of the radius vector of the revolving particle P, in each case.
View SolutionFigures depicts two circular motions. The radius of the circle, the period of revolution, the initial position and the sense of revolution are indicated on the figures. Obtain the simple harmonic motions of the x-projection of the radius vector of the rotating particle P in each case.
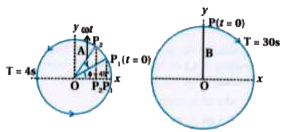
View SolutionFigures 14.25 correspond to two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution (i.e. clockwise or anti-clockwise) are indicated on each figure.

Obtain the corresponding simple harmonic motions of the x-projection of the radius vector of the revolving particle P, in each case.
View Solution
