Find the frequency of small oscillations of the arrangement illustrated in figure. The radius of the pulley is R, its moment of inertia relative to the rotation axis is I, the mass of the body is m, and the spring stiffness is x.The mass of the thread and the spring is negligible , the thread does not slide over the pulley, there is no friction in the axis of the pulley
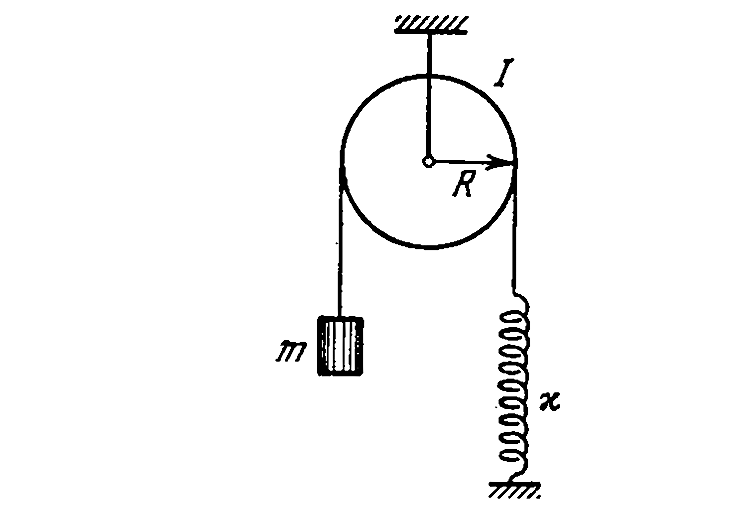
The physical system consists with a pulley and the block . Choosing an intertial frame, let us direct the x− axis as shown in the figure.
Initially the system is in equilibrium position. Now from the condition of translation equilibrium for the block
T0=mg...(1)
Similarly for the rotational equiliibrium of the pulley
dΔ/R=T0R
or, T0kΔl....(2)
from Eqns. (1) and (2) Δl=mgk...(3)
Now let us disturb the equilibrium of the system no matter in which way to analyse its motion. As an arbitrary position shown in the figure, from Newton's second law of motion or the block .
Fx=mwx
mg−T=mw=m..x...(4)
Similarly for the pulley
Nz=Iβz
TR−k(Δl+x)R=I..θ....(5)
But w=βR or,.x=R..θ...(6)
from (5) and (6) TR=k(Δl+x)R=IR..x...(7)
Solving (4) and (7) using the initial condition of the problem
−kRx=(mR+IR)..x
or, ..x=−⎛⎜⎝km+lR2⎞⎟⎠
Hence the sought time period, T=2πω0=2π√m+l/R2k
Note : we may solve this problem by using the conservation of mechanical energy also

Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electric Oscillations
56 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Elastic Waves
39 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
In the arrangement shown in figure a weight A possesses mass m, a pulley B possesses mass M. Also known are the moment of inertia I of the pulley relative to its axis and the radii of the pulley R and 2R. The mass of the threads is negligible. Find the acceleration of the weight A after the system is set free.

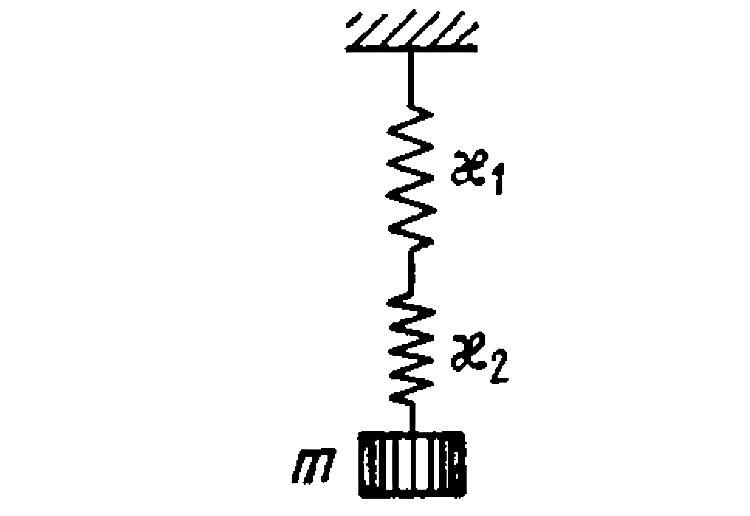
View SolutionFind the period of small vertical oscillations of a body with mass m in the system illustrated in figure. The stiffness values of the springs are x1 and x2, their masses are negligible.
View SolutionFind the frequency of small oscillatinos of a thin uniform vertical rod of mass m and length l hinged at the point O (figure). The combined stiffness fo the springs is equal to x. The mass of the springs is negligible.
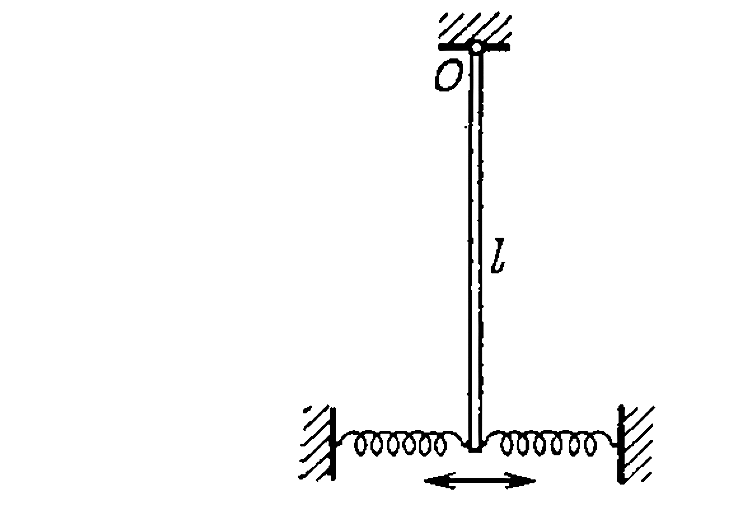
View SolutionSolve the previous problem if the pulley has a moment of inertia I about its axis and the string does not slip over it.
View SolutionAssuming the moment of inertia of the pulley to be I and its radius to be r.
View SolutionFind the acceleration of the block of mass m in the arrangement shown in the following figures. The masses of the pulleys and the threads, as well as the friction are assumed to be negligible.

View SolutionThe pulley shown in figure has a moment of inertias I about its xis and mss m. find the tikme period of vertical oscillastion of its centre of mass. The spring has spring constant k and the string does not slip over the pulley.

View SolutionIn the arrangement shown in figure the masses of the wedge M and the body m are known. The appreciable friction exists only between the wedge and the body m, the friction coefficient being equal to k. The masses of the pulley and the thread are negligible. Find the acceleration of the body m relative to the horizontal surface on which the wedge slides.

View SolutionIn the figure, the massless and inextensible thread does not slip on the pulley. It is wound over pulley as shown. If the system is released from rest,
View SolutionThe pulley shown in figure has a moment of inertias I about its xis and mss m. find the tikme period of vertical oscillastion of its centre of mass. The spring has spring constant k and the string does not slip over the pulley.

View Solution
