Find the image shift if the paperweight is inverted at its place so that the spherical surface touches the paper
The correct Answer is:A, C
To solve the problem of finding the image shift when the paperweight is inverted so that the spherical surface touches the paper, we can follow these steps:
1. Understanding the Setup:
- The paperweight has a spherical surface that is now in contact with the paper. When the spherical surface touches the paper, the light rays reflecting off the surface will create an image that appears shifted.
2. Identify the Refractive Indices:
- The refractive index of glass (μg) is typically around 1.5.
- The refractive index of air (μa) is approximately 1.
3. Determine the Thickness:
- The thickness (t) of the glass in this case is equal to the radius of the spherical surface. Given that the radius is 3 cm, we have:
t=3cm
4. Use the Image Shift Formula:
- The formula for the image shift (Δt) when light passes through a medium is given by:
Δt=t(1−1μ)
- Here, we will use the refractive index of glass (μg = 1.5).
5. Substituting Values:
- Substitute the values into the formula:
Δt=3cm(1−11.5)
6. Calculating the Shift:
- First, calculate 1−11.5:
1−11.5=1−23=13
- Now, substitute this back into the equation for Δt:
Δt=3cm×13=1cm
7. Conclusion:
- The image shift when the paperweight is inverted and the spherical surface touches the paper is 1 cm.
Final Answer:
The image shift is 1 cm.
---
- The paperweight has a spherical surface that is now in contact with the paper. When the spherical surface touches the paper, the light rays reflecting off the surface will create an image that appears shifted.
- The refractive index of glass (μg) is typically around 1.5.
- The refractive index of air (μa) is approximately 1.
- The thickness (t) of the glass in this case is equal to the radius of the spherical surface. Given that the radius is 3 cm, we have:
t=3cm
- The formula for the image shift (Δt) when light passes through a medium is given by:
Δt=t(1−1μ)
- Here, we will use the refractive index of glass (μg = 1.5).
- Substitute the values into the formula:
Δt=3cm(1−11.5)
- First, calculate 1−11.5:
1−11.5=1−23=13
- Now, substitute this back into the equation for Δt:
Δt=3cm×13=1cm
- The image shift when the paperweight is inverted and the spherical surface touches the paper is 1 cm.
The image shift is 1 cm.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXAMPLE
9 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer
18 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Objective -2
7 Videos
- GAUSS LAWBOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Short Question
7 Videos
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer
11 Videos
Similar Questions
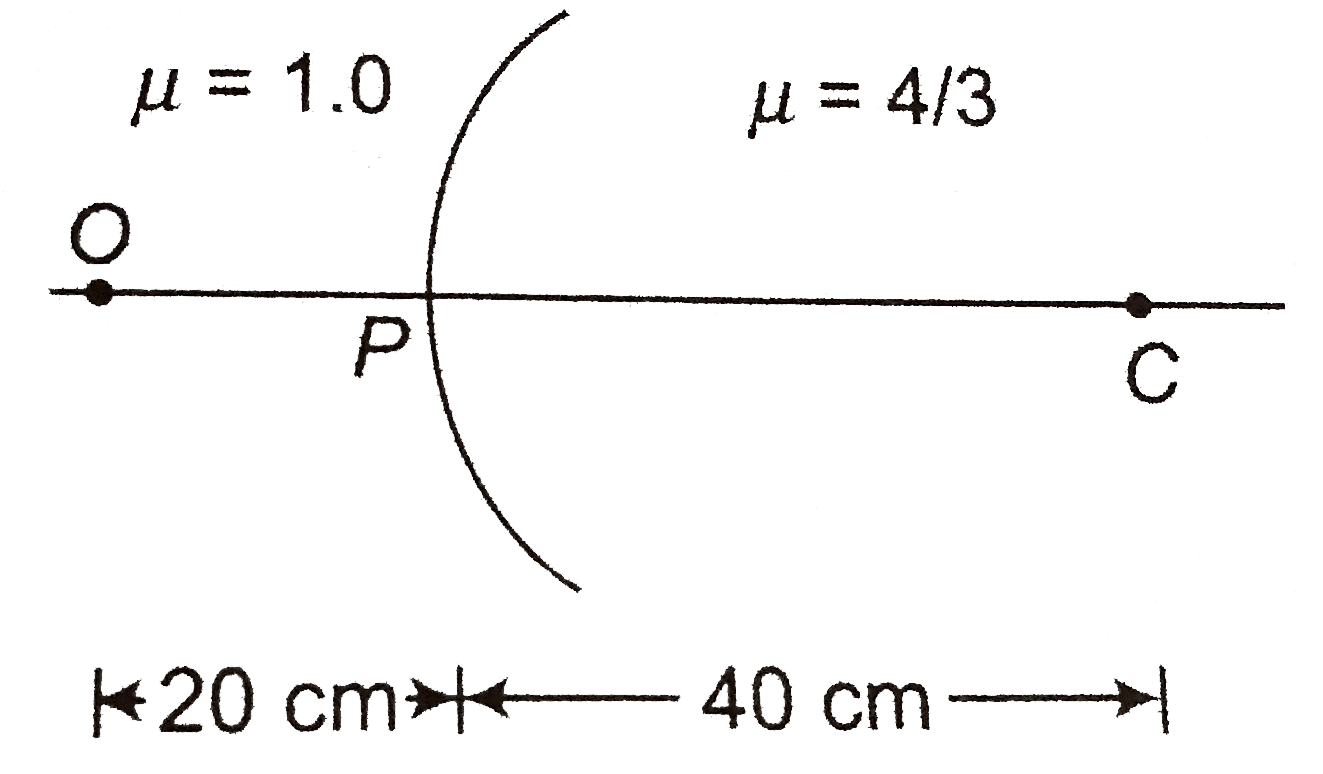
Locate the image of the point object O. The point C is centre of curvature of the spherical surface.
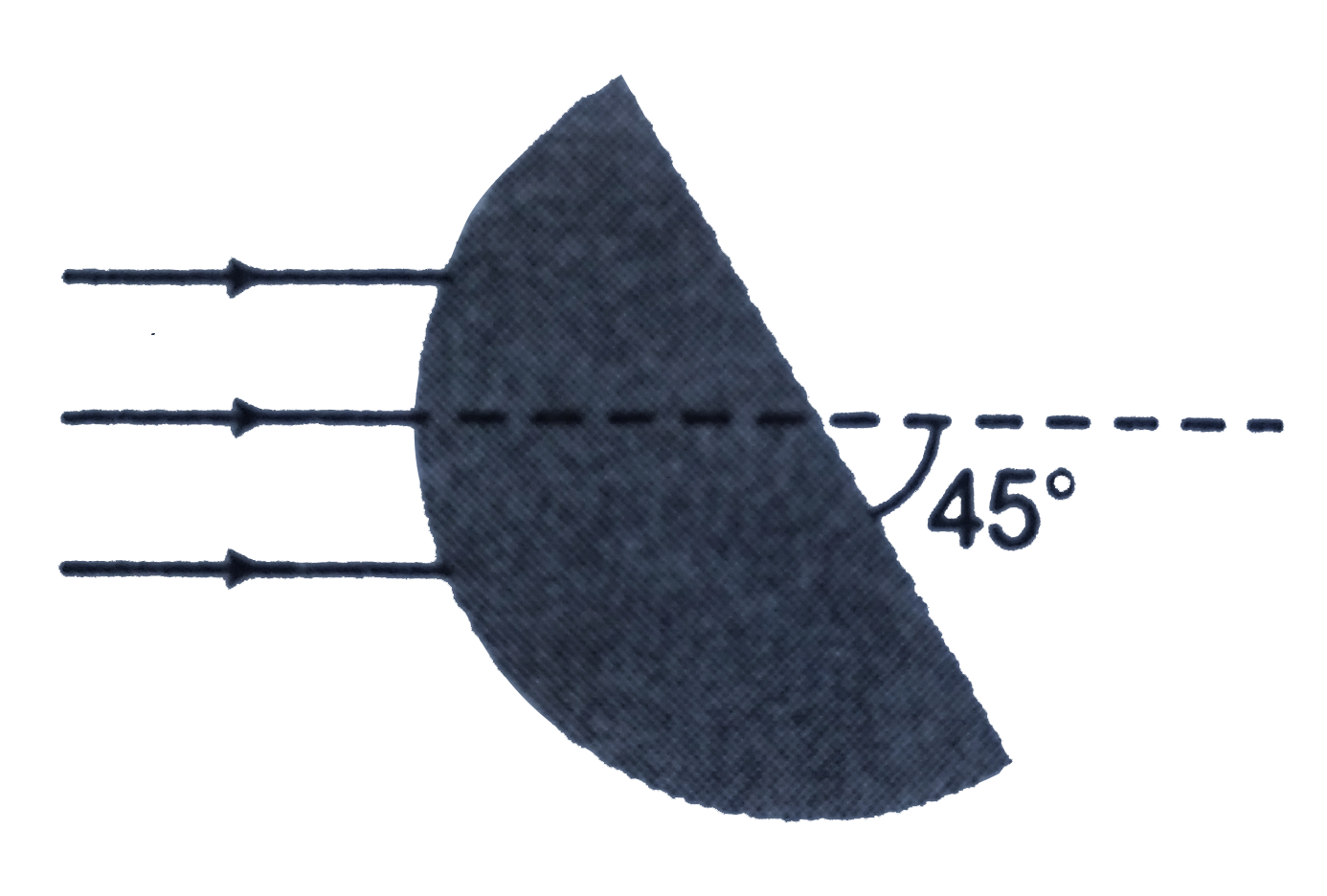
View SolutionA parallel narrow beam of light is incident on the surface of a transparent hemisphere of radius R and refractive index μ=1.5 as shown. The position of the image formed by refraction at the image formed by refraction at the spherical surface only as
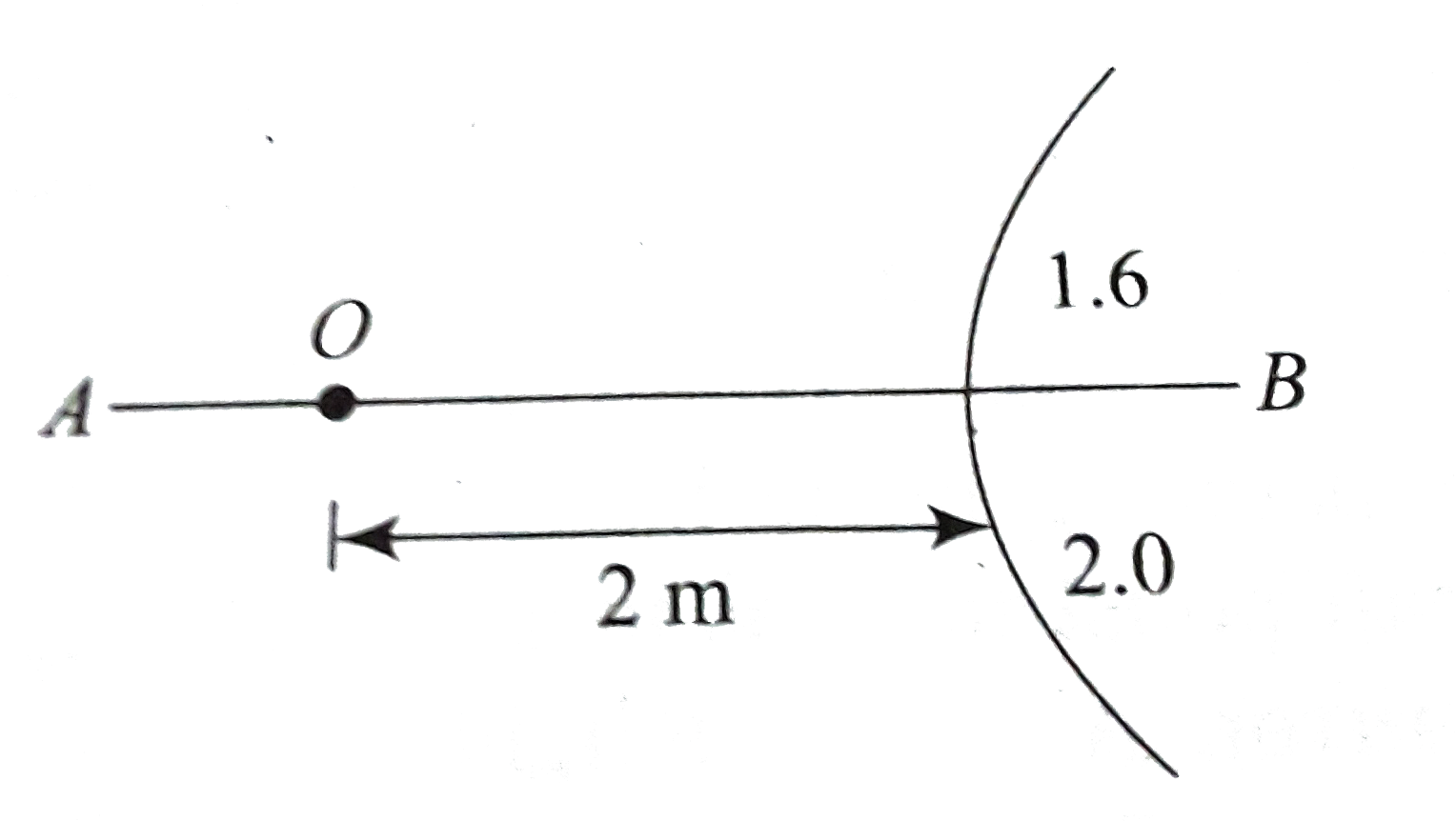
View SolutionIn Figure, a point object O is placed in air. A spherical boundary separates two media. Ab is the principall axis. The refractive index above AB is 1.6 and below AB is 2.0. The separation between the images formed due to refraction at a the spherical surface is (assume the radius of curvature (R) to be 1 unit)
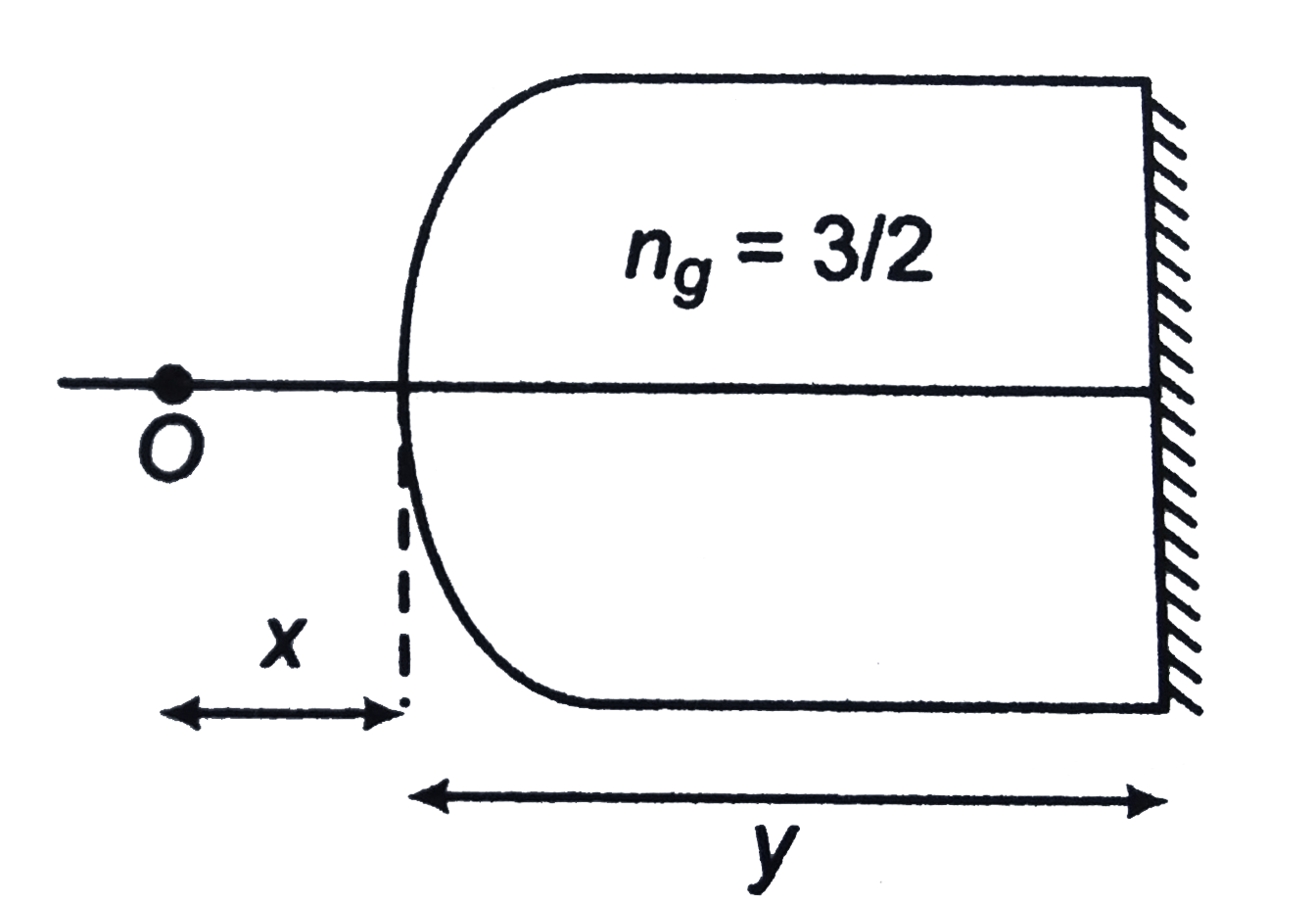
View Solution(a) A point object, O is on the principle axis of a spherical surface having a radius of curvature, R. Draw a diagram to obtain the relation between the object and image distances, the refractive indicess of the media and the radius of curvature of the spherical surface.
View SolutionIn the figure shown , a point object O is placed in air on the principal axis. The radius of curvature of the spherical surfaces is 60cm. I is the final image formed after all reflections and refractions.
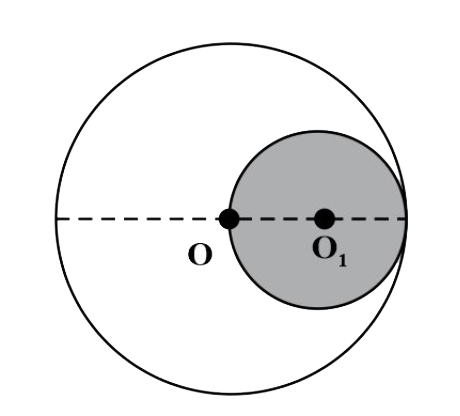
View SolutionA spherical cavity is made in a lead sphere of radius R such that its surface touches the outsides surface of lead sphere and passes through the centre. The shift in the centre of mass of the lead sphere as a result of this following, is
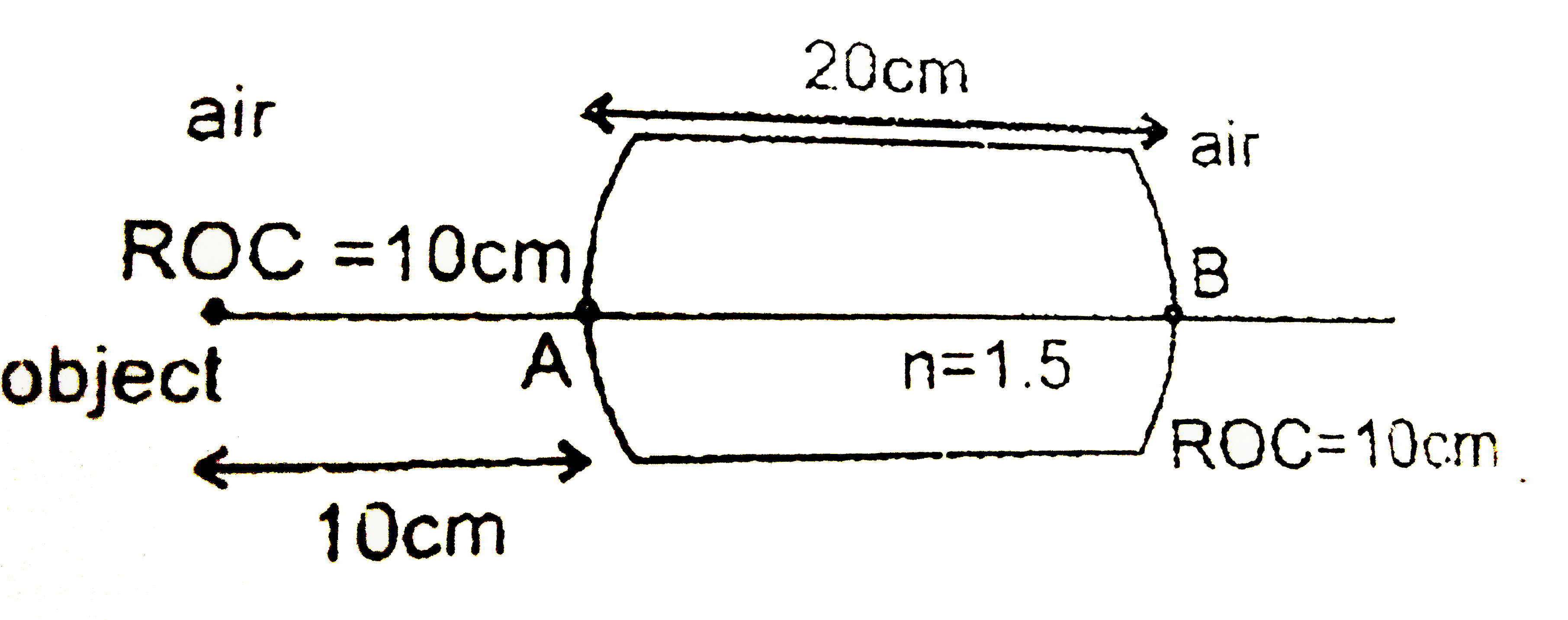
View SolutionAn object is placed 10cm away form a glass piece (n=1.5) of length 20cm bounded by spherical surfaces of radii of curvaure 10cm. Find the position of final image formed after two refractions at the spherical surfaces.
View SolutionFigure below shows a parallel beam of monochromatic light incident on a convex spherical surface, radius of curvature R = 30 cm, which separates glass (refractive index - 1 6) from air. Find the position of the image formed due to refraction of light at this single spherical surface.

View SolutionA metallic spherical shell has an inner radius R1 and outer radius R2. A charge is placed at the centre of the spherical cavity. The surface charge density on the inner surface is

View SolutionWhen an object is placed 60cm in front of a diverging lens, a virtual image is formed 20cm from the lens. The lens is made of a refractive index μ=1.65 and its two spherical surfaces have the same radius of curvature. What is the value of this radius?
View Solution
