A paperweight in the form of a hemisphere of radius 3.0 cm is used to hold down a printed page. An observer looks at the page vertically through the paperweight. At what height above the page will the printed letters near the centre appear to the observer ?
The correct Answer is:B, D
To solve the problem, we need to determine the height above the page at which the printed letters appear to the observer when viewed through a hemispherical paperweight.
1. Identify Given Data:
- The radius of the hemisphere (R) = 3.0 cm.
- The observer looks at the page vertically through the paperweight.
2. Understand the Refraction Process:
- The light from the printed letters travels through two interfaces:
1. The flat surface of the hemisphere (air to glass).
2. The curved surface of the hemisphere (glass to air).
3. Calculate Image Distance for the Flat Surface:
- For the flat surface:
- Refractive index of air (μ1) = 1
- Refractive index of glass (μ2) = 1.5
- Object distance (U) = 0 (since the object is at the center of the hemisphere).
- Radius of curvature (R) = ∞ for a flat surface.
- Using the formula:
μ2V−μ1U=μ2−μ1R
- Substituting the values:
1.5V−10=1.5−1∞
- Since U=0, the left side becomes undefined, but we can conclude that the image distance (V) for the flat surface is at the same point, hence V=0.
4. Calculate Image Distance for the Curved Surface:
- For the curved surface:
- Refractive index of glass (μ1) = 1.5
- Refractive index of air (μ2) = 1
- Object distance (U) = -3 cm (measured from the pole of the curved surface).
- Radius of curvature (R) = -3 cm (since it is a concave surface).
- Using the same formula:
1V−1.5−3=1−1.5−3
- Rearranging gives:
1V+0.5=−0.5−3
- Simplifying:
1V+0.5=16
- Thus:
1V=16−0.5=16−36=−26=−13
- Therefore:
V=−3 cm
5. Conclusion:
- The image is formed at the same position as the object, which means the printed letters appear to be at the same height above the page, which is 3 cm.
Final Answer:
The printed letters near the center appear to the observer at a height of 3.0 cm above the page.
---
- The radius of the hemisphere (R) = 3.0 cm.
- The observer looks at the page vertically through the paperweight.
- The light from the printed letters travels through two interfaces:
1. The flat surface of the hemisphere (air to glass).
2. The curved surface of the hemisphere (glass to air).
- For the flat surface:
- Refractive index of air (μ1) = 1
- Refractive index of glass (μ2) = 1.5
- Object distance (U) = 0 (since the object is at the center of the hemisphere).
- Radius of curvature (R) = ∞ for a flat surface.
- Using the formula:
μ2V−μ1U=μ2−μ1R
- Substituting the values:
1.5V−10=1.5−1∞
- Since U=0, the left side becomes undefined, but we can conclude that the image distance (V) for the flat surface is at the same point, hence V=0.
- For the curved surface:
- Refractive index of glass (μ1) = 1.5
- Refractive index of air (μ2) = 1
- Object distance (U) = -3 cm (measured from the pole of the curved surface).
- Radius of curvature (R) = -3 cm (since it is a concave surface).
- Using the same formula:
1V−1.5−3=1−1.5−3
- Rearranging gives:
1V+0.5=−0.5−3
- Simplifying:
1V+0.5=16
- Thus:
1V=16−0.5=16−36=−26=−13
- Therefore:
V=−3 cm
- The image is formed at the same position as the object, which means the printed letters appear to be at the same height above the page, which is 3 cm.
The printed letters near the center appear to the observer at a height of 3.0 cm above the page.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXAMPLE9videos
GEOMETRICAL OPTICS
- BOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer18videos
GEOMETRICAL OPTICS
- BOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Objective -27videos
GEOMETRICAL OPTICS
- BOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Short Question7videos
GAUSS LAW
- BOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer11videos
LIGHT WAVES
Similar Questions
A glass sphere has radius of 5.0cm and a refractive index of 1.6. A paperweight is constructed by slicing through the sphere on a plate that is 2.0cm from the centre of the sphere and perpendicular to radius of the sphere that passes through the centre of the circle formed by the intersection of the plane and the sphere. The paperweight is placed on a table and viewed from directly above an observer who is 8.0cm from the table top, as shown in figure. When viewed through the paperweight, how far away does the table top appear to the observer?
View SolutionA printed page is kept pressed to a glass cube (μ=1.5) of edge 6.0 cm. By what amount will the printed letters appear to the shifted when viewed from the top?
View SolutionA printed page is kept pressed by a glass cube (µ=1.5) of edge 9.0 cm. By what amount will the printed letters appear to be shifted when viewed from the top?
View SolutionThe total area of page is 150cm2. The combined width of the margin at the top and bottom is 3 cm and the side 2 cm. What must be the dimensions of the page in order that the area of the printed matter may be maximum ?
View SolutionThe total area of a page is 150cm2. The combined width of the margin at the top and bottom is 3cm and the side 2cm. What must be the dimensions of the page in order that the area of the printed matter may be maximum?
View SolutionThe total area of a page is 150cm2. The combined width of the margin at the top and bottom is 3cm and the side 2cm. What must be the dimensions of the page in order that the area of the printed matter may be maximum?
View SolutionA glass sphere of (μ=1.5) with a radius of 15.0cm has a tiny air bubble 5cm above its centre. The sphere is viewed looking down along the extended radius containing the bubble. What is the apparent depth of the bubble below the surface of the sphere?
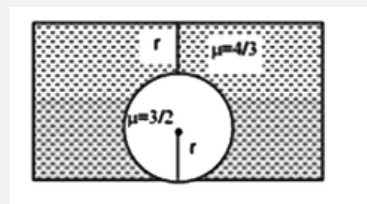
View SolutionA glass sphere having refractive index (3/2) is having a small irregularity at its centre. It is placed in a liquid of refractive index 43 such that the surface of the liquid is at a distance r above the sphere, where r = 20 cm is radius of the sphere, where r = 20 cm is radius of the sphere. If the irregularity is viewed from above then what is it's distance (in cm) from the centre where eye will observed the irregularity?
 View Solution
View SolutionA point source of light S is placed at the bottom of a vessel containg a liquid of refractive index 5/3. A person is viewing the source from above the surface. There is an opaque disc of radius 1cm floating on the surface. The centre of the disc lies vertically above the source S. The liquid from the vessel is gradually drained out through a tap. What is the maximum height of the liquid for which the source cannot at all be seen from above?
View SolutionA container contains water up to a height of 20 cm and there is a point source at the centre of the bottom of the container. A rubber ring of radius r floats centrally on the water. The ceiling of the room is 2.0 m above the water surface. (a) Find the radius of the shadow of the ring formed on the ceiling if r = 15 cm. (b) Find the maximum value of r for which the shadow of the ring is formed on the ceiling. Refractive index of water =4/3.
View Solution

