Find the location of centre of mass of a uniform semicirular plate of radius R and mass M.
Video Solution
Text Solution
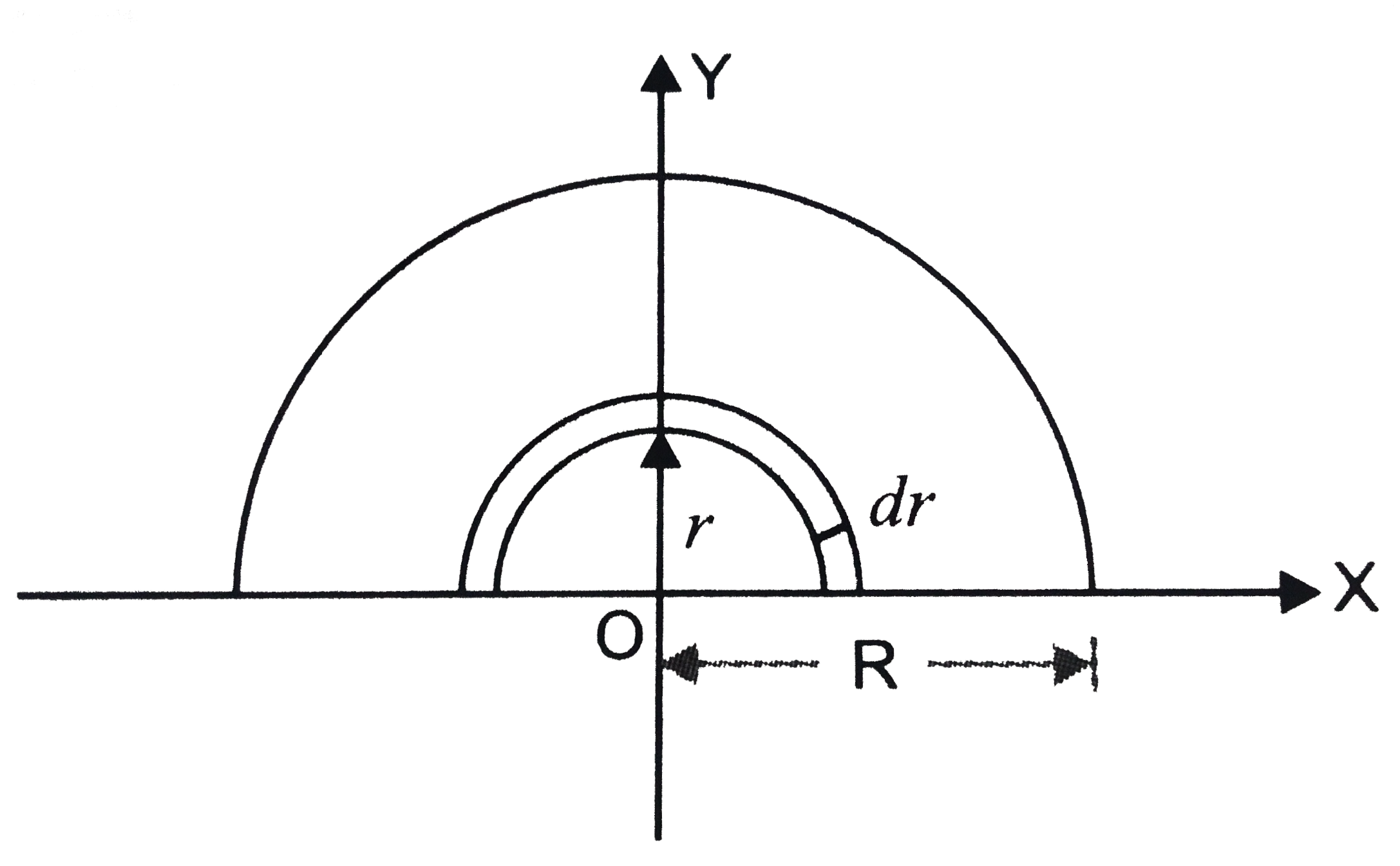
In Fig. we have chosen XY axes with the origin at O, the centre of semicirular disc. By origin symmetry, the centre of mass would lie on Y-axis. Thus xcm=0, and
ycm=1M∫ydm …(i)
If σ mass per unit area of the disc, then
σ=MπR2/2=2MπR2
The semicirular plate can be supposed to be made up of a large number of semicircular strips, each of mass dm and radii ranging from r=0 to r=R. Consider one such semicirular strip of radius r and thickness dr as shown in Fig.
Surface area of this element =πr(dr)
∴ Mass of this element, dm=σ×πrdr
=(2MπR2)πrdr
dm=2MR2rdr
The co-ordinates of CM of this element
(x,y)=(0,2rπ)
Therefore, for semicirular plate
ycm=1M∫R0ydm
=1M∫R02rπ.(2MR2rdr)
ycm=4πR2[r33]R0=4R3π
Hence centre of mass of uniform semicirular plate is
(0,4R3π)
|
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:NCERT
Explore 21 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:ADDITIONAL EXERCISES
Explore 11 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:SOLVED EXAMPLES TYPE E
Explore 1 Video
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(a)
Explore 25 Videos
- THERMODYNAMICSBook:PRADEEPChapter:THERMODYNAMICSExercise:Assertion- Reason Type Questions
Explore 19 Videos
Similar Questions
Knowledge Check
Find the position of centre of mass of a uniform disc of radius R from which a hole of radius is cut out. The centre of the hole is at a distance R/2 from the centre of the disc.
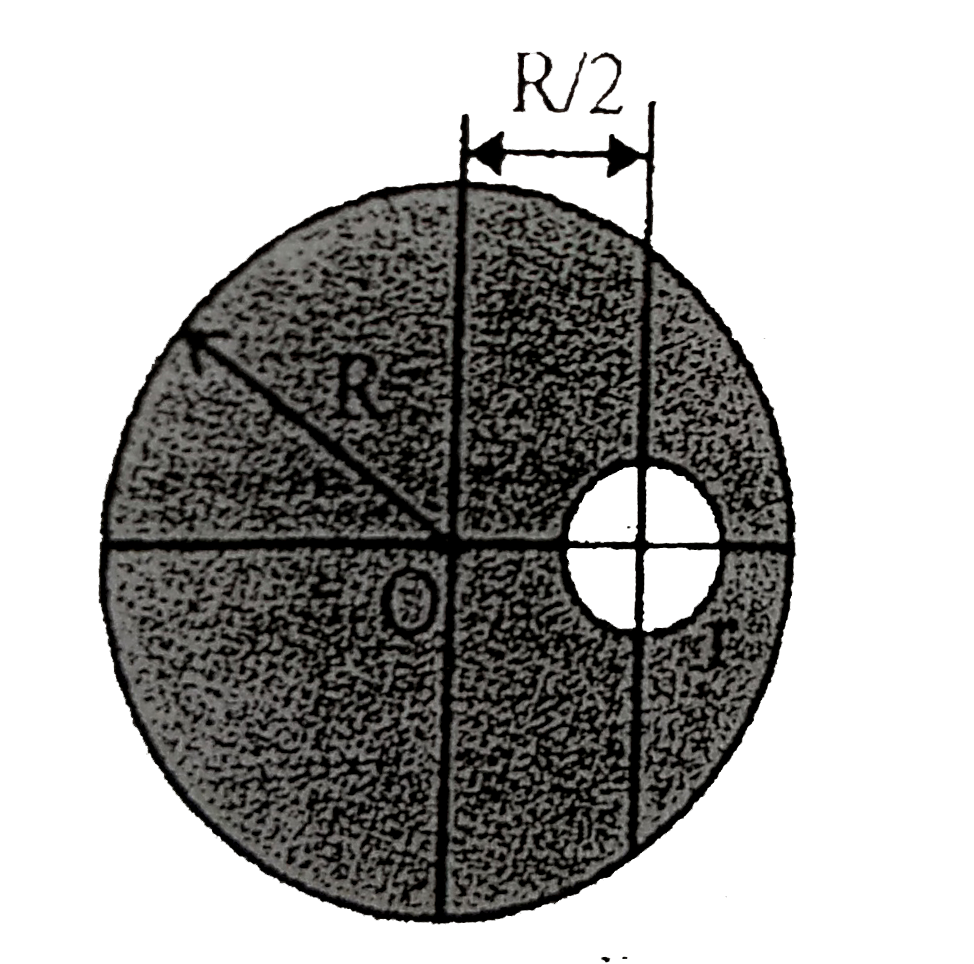 ARr22(R2−r2) towards right of OBRr22(R2−r2) towards left of OC2Rr2(R2+r2) towards right of OD2Rr2(R2+r2) towards left of O
ARr22(R2−r2) towards right of OBRr22(R2−r2) towards left of OC2Rr2(R2+r2) towards right of OD2Rr2(R2+r2) towards left of OFind the coordinates of centre of mass of a uniform semicircular closed wire frame with respect to the origin which is at its centre. Radius of the circular portion is R
 A(4R3π,0)B(2Rπ+2,0)C(2Rπ,0)D(Rπ+2,0)
A(4R3π,0)B(2Rπ+2,0)C(2Rπ,0)D(Rπ+2,0)In the figure shown, find out centre of mass of a system of a uniform circular plate of radius 3R from O in which a hole of radius R is cut whose centre is at 2R distance from the centre of large circular plate
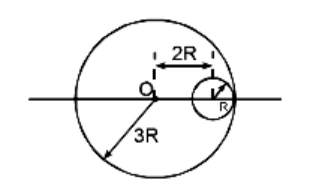 A(a) R2B(b) R5C(c) R4D(d) None of these
A(a) R2B(b) R5C(c) R4D(d) None of these
Find the centre of mass of a homogeneous semicircular plate of radius a.
View SolutionDetermine the centre of mass of a uniform hemisphere of radius R.
View SolutionFind the centre of mass of a uniform solid cone.
View SolutionFind the centre of mass of a uniform triangula lamina.
View SolutionFind coordinates of mass center of a uniform semicircular plate of radius r placed symmetric to the y-axis of a Cartesian coordinate system, with centre at origin.
View Solution
