Find the moment of inertia of a uniform square plate of mass M and edge a about one of its diagonals.
Video Solution
Text Solution
The correct Answer is:A, B
Let small sectional area is at a distance d from xx' axils therefore mass at tehat small section =ma2×a×dx

Therefore moment of inertia about xx' axis
I×'=2∫a20ma2×(adx)×x2
=2×ma[x33]a20
=2×ma[a33×8]=ma312
therefore, Izz=I×+Iyy
=2×(ma212)=ma26
since the two diagoN/Als are perpendicular to each other therefore
Izz=I×+Iyy<br>rarr (ma^2)/6=2xxI_(xx) (I_(xx)=I_(yy))<br>rarr I_(xx)=(ma^2)/12
|
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective 2
15 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises
51 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
Similar Questions
Knowledge Check
The radius of gyration of a uniform square plate of mass M and side a about its diagonal is
Aa√6Ba2√3Ca2√2Da4The moment of inertia of a uniform circular disc of mass M and of radius R about one of its diameter is
A14MR2B12MR2C23MR2D25MR2The moment of inertia of a cube of mass m and side a about one of its edges is equal to
A23ma2B43ma2C3ma2D83ma2
Find the moment of inertia of a uniform square plate of mass M and edge of length 'l' about its axis passing through P and perpendicular to it.

View SolutionFind the moment of inertia of a uniform rign of mass M and radius R about a diameter.
View SolutionFind the moment of inertia of uniform ring of mass M and radius R about a diameter.
View SolutionFind the moment of inertia of a uniform rectangular plate of mass M and edges of length 'I' and 'b' about its axis passing through the centre and perpendicular to it.
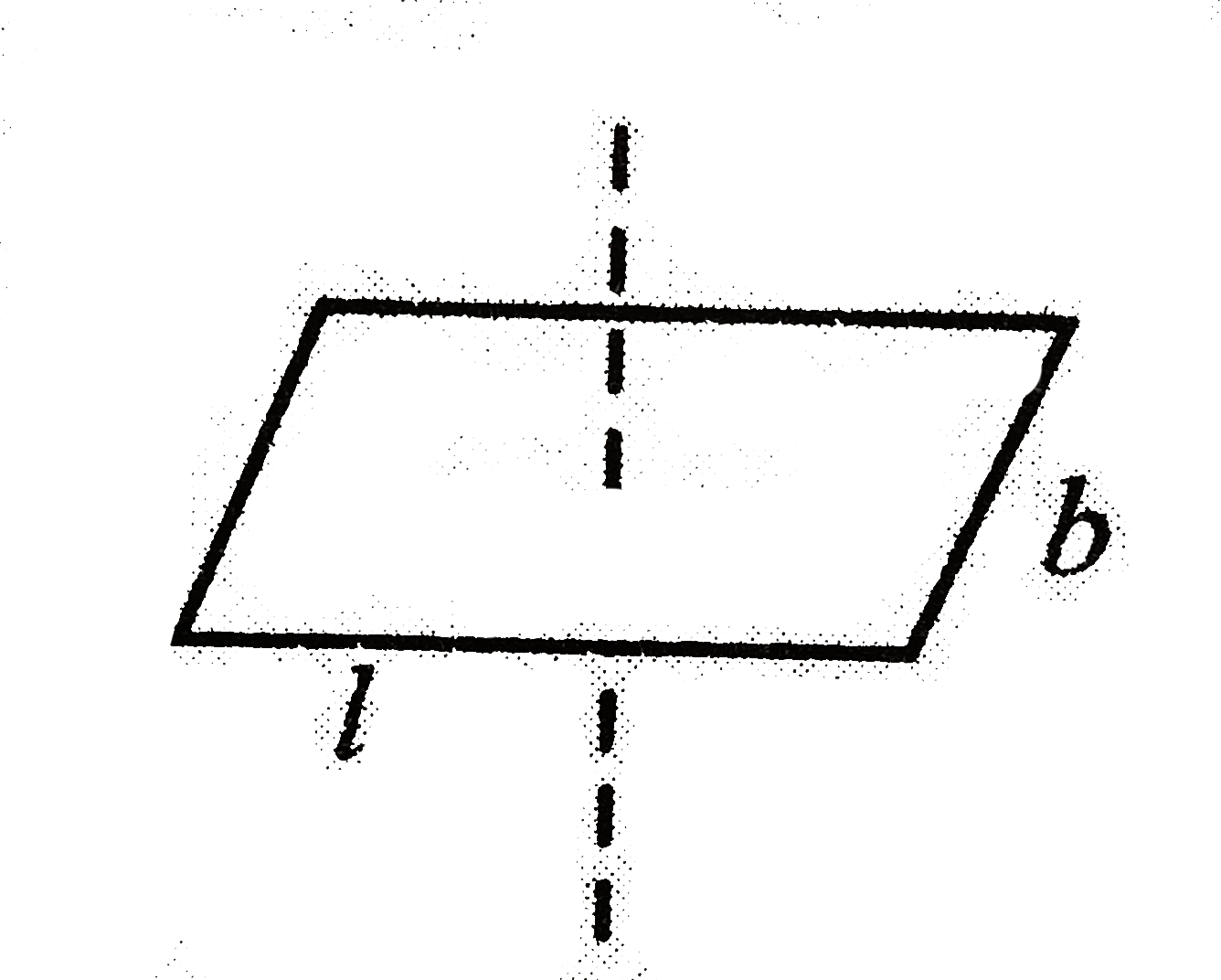
View SolutionFind the moment of inertia of a uniform sphere of mass m and radius R about a tangent if the spheres (1) solid (ii) hollow?
View Solution
