Find the period of small oscillations of a mathematical pendulum of length l if its point of suspension O moves relative to the Earth's surface in an arbitrary directio with a constant acceleration w (figure). Calculate that period if l=21cm,w=g/2, and the angle between the vectors w and g equals beat=120∘.
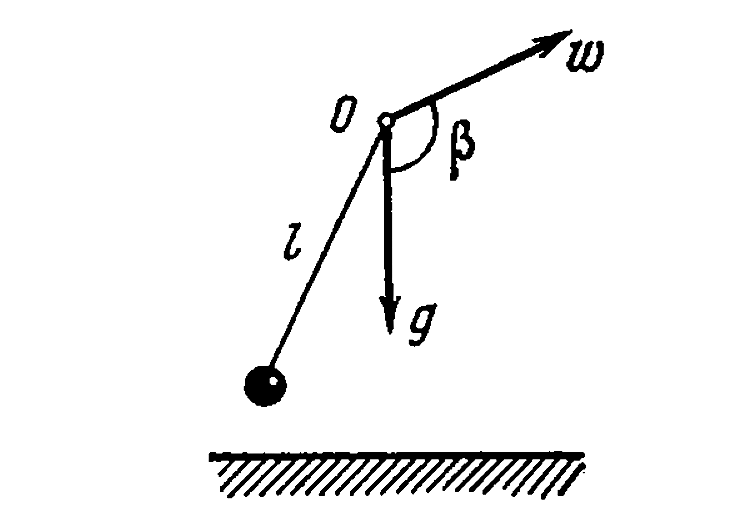
In the frame of point of suspension the mathematical pendulum of mass m (say) will oscillate. In this fracem, the body m will experience the inertial force m(−→w) in addition to the real forces during its oscillations. Therefore in equilibrium position m is deviated by some angle say α. In equilibrium position.
T0cosα=mg+mwcos(π−β) and T0sinα=mwsin(π−β)
So, from these two two Eqns
tanα=g−wcosβwsinβ
and cosα=√m2w2sin2β+(mg−mwcosβ)2mg−mwcosβ....(1)
Let us displace the bob m from its equilibrium position by some small angle and then release it. Now locate the ball at an angular position (α+θ) from vertical as shown in the figure.
From the Eqn. : N0z=Iβz
=−mglsin(α+θ)−mwcos(π−β)lsin(α=θ)+mwsin(π−β)lcos(α+θ)=ml2..θ
or , −g(sinαcosθ+cosαsinθ)−wcos(π−β)(sinαcosθ+cosαsinθ+wsinβ(cosαcosθ−sinαsinθ)
=l..θ
But for small
θ,sinθ≅θcosθ≅1
So, −g(sinα+cosαθ)−wcos(π−β)(sinα+cosαθ)=wsinβ(cosα−sinαθ)
=l..θ
or (tanα+θ)(wcosβ−g)+wsinβ(1−tanαθ)=lcosα..θ...(2)
Solving Eqns (1) and (2) simultaneously we get
−(g2−2wgcosβ+w2)θ=l√g2+w2−2wgcosβ..θ
Thus ..θ=−|→g−→w|lθ
Hence the sought time period T=2πω0=2π√l|→g−→w|

Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electric Oscillations
56 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Elastic Waves
39 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
Find the period of oscillation of a pendulum of length l if its point of suspension is
(a) moving vertically up with acceleration a
(b) moving vertically down with acceleration a(<g)
(c) failing freely under gravity
moving horizontal with acceleration a.
View SolutionA top of mass m=1.0kg and moment of inertia relative to its own axis I=4.0g⋅m2 spins with an angular velocity ω=310rad/s. Its point of rest is located on a block which is shifted in a horizontal direction with a constant acceleration w=1.0m/s2. The distance between the point of rest and the centre of inertia of the top equals l=10cm. Find the magnitude and direction of the angular velocity of precession ω′.
View Solution
Knowledge Check
The period of small oscillations of a simple pendulum of length l if its point of suspension O moves a with a constant acceleration α=α1∧i−α2∧j with respect to earth is (∧i and ∧j are unit vectors in horizontal in horizontal and vertically upward directions respectively)
AT=2π ⎷l{(g−α2)2+α21}1/2BT=2π ⎷l{(g−α1)2+α22}1/2CT=2π√lgDT=2π ⎷l(g2+α21)1/2The period of small oscillations of a simple pendulum of length l if its point of suspension O moves a with a constant acceleration α=α1∧i−α2∧j with respect to earth is (∧i and ∧j are unit vectors in horizontal in horizontal and vertically upward directions respectively)
AT=2π ⎷l{(g−α2)2+α21}1/2BT=2π ⎷l{(g−α1)2+α22}1/2CT=2π√lgDT=2π ⎷l(g2+α21)1/2The period of a conical pendulum in terms of its length (l) , semivertical angle (θ) and acceleration due to gravity (g) is
A12π√lcosθgB12π√lsinθgC2π√lcosθgD4π√ltanθg
The period of a pendulum whose suspension is stationary relative to the Earth's surface is 1.50 s. What will its period be, if it is placed in a car moving horizontally with an acceleration of 4.9m/s2? What will be the change in the pendulum's angle of equilibrium?
View SolutionThe period of oscillation of a simple pendulum of length L suspended from the roof of a vehicle which moves without frication down on inclined plane of inclination lpha=60∘ is given by π√XLg then find X.
View SolutionFind the period of small oscillations in a vertical plane performed by a ball of mass m=40g fixed at the middle of a horizontallly stretched string l=1.0m in length. The tension of the string is assumed to be constant and equal to F=10N.
View SolutionThe period of oscillation T of a pendulum of length l at a place of acceleleration due to gravity g is given by T=2π√lg. If the calculated length is 0.992 times the actual length and if the value assumed for g is 1.002times its actal value, the relative error in the computed value of T, is
View SolutionA simple pendulum 50cm long is suspended from the roof of a acceleration in the horizontal direction with constant acceleration √3gm/s−1. The period of small oscillations of the pendulum about its equilibrium position is (g=π2m/s2) ltbRgt
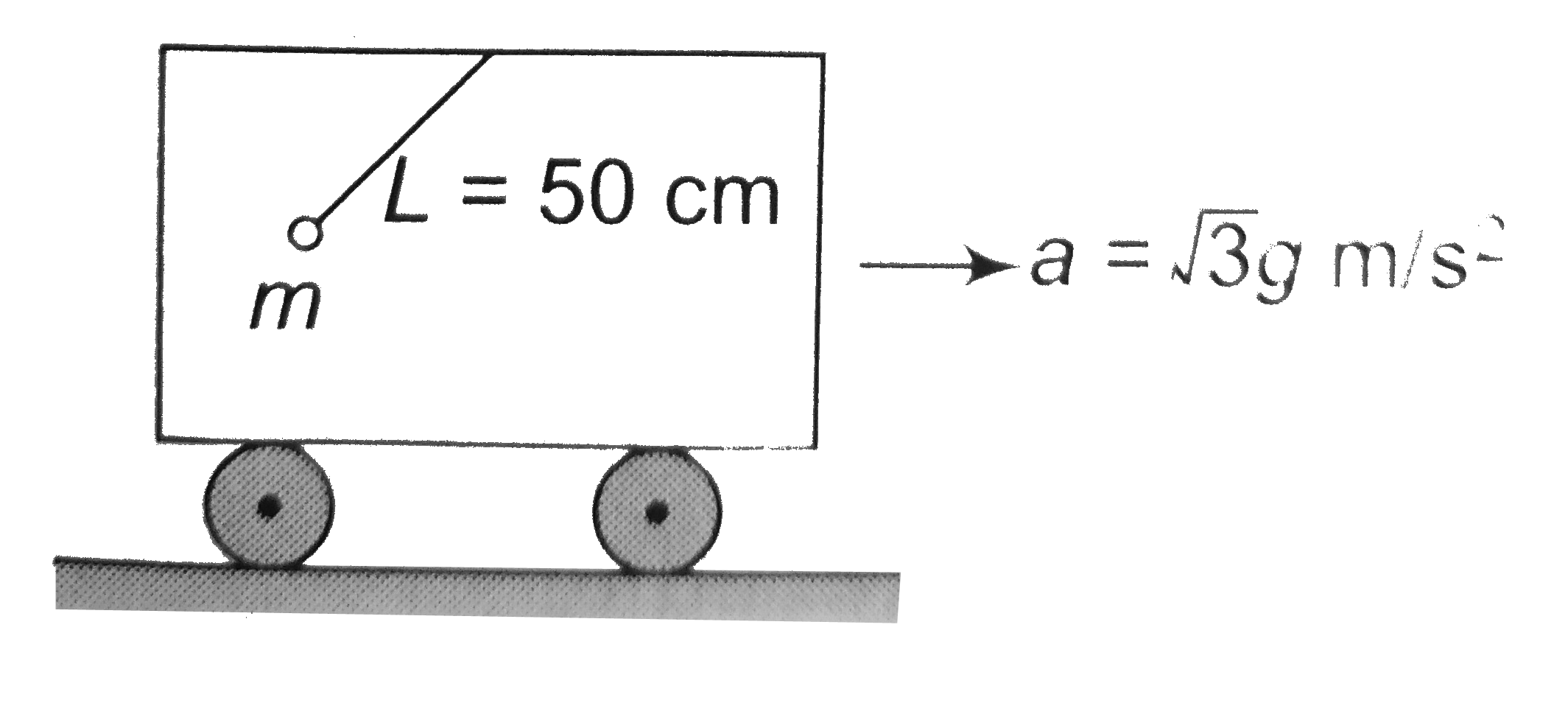
View Solution
