Find the ratio of magnetic dipole moment and magnetic field at the centre of a disc. Radius of disc is R and it is rotating at constant angular speed o about its axis. The disc is insulating and uniformly charged
The correct Answer is:B, C
To find the ratio of the magnetic dipole moment (M) to the magnetic field (B) at the center of a uniformly charged disc rotating with a constant angular speed (ω), we can follow these steps:
Step 1: Define the Magnetic Dipole Moment (M)
The magnetic dipole moment (M) for a rotating charged disc can be expressed as:
M=I⋅A
where I is the current and A is the area of the disc.
Step 2: Calculate the Area (A) of the Disc
The area A of a disc with radius R is given by:
A=πR2
Step 3: Determine the Current (I)
The current I can be defined in terms of the charge Q and the frequency f of rotation. The frequency f is related to the angular speed ω by:
f=ω2π
Thus, the current I can be expressed as:
I=QT=Q⋅f=Q⋅ω2π
Step 4: Substitute Current into the Magnetic Dipole Moment Equation
Substituting the expression for current into the equation for magnetic dipole moment:
M=I⋅A=(Q⋅ω2π)⋅(πR2)
This simplifies to:
M=QωR22
Step 5: Calculate the Magnetic Field (B) at the Center of the Disc
The magnetic field B at the center of a rotating disc can be derived from the Biot-Savart law. For a small disc, the magnetic field dB can be expressed as:
dB=μ02⋅dIR
where dI is the differential current.
Step 6: Express the Differential Current (dI)
The differential current dI can be expressed in terms of the charge density:
dI=dQdt=QπR2⋅2πr⋅f
where r is the radius from the center to the differential area.
Step 7: Integrate to Find Total Magnetic Field
Integrating dB from 0 to R:
B=∫R0dB=μ02⋅∫R0Q⋅ω2πR⋅2πrdr
This leads to:
B=μ0ωQ4πR
Step 8: Find the Ratio MB
Now, we can find the ratio of the magnetic dipole moment to the magnetic field:
MB=QωR22μ0ωQ4πR
This simplifies to:
MB=2πR3μ0
Final Result
Thus, the ratio of the magnetic dipole moment to the magnetic field at the center of the disc is:
MB=πR32μ0
---
The magnetic dipole moment (M) for a rotating charged disc can be expressed as:
M=I⋅A
where I is the current and A is the area of the disc.
The area A of a disc with radius R is given by:
A=πR2
The current I can be defined in terms of the charge Q and the frequency f of rotation. The frequency f is related to the angular speed ω by:
f=ω2π
Thus, the current I can be expressed as:
I=QT=Q⋅f=Q⋅ω2π
Substituting the expression for current into the equation for magnetic dipole moment:
M=I⋅A=(Q⋅ω2π)⋅(πR2)
This simplifies to:
M=QωR22
The magnetic field B at the center of a rotating disc can be derived from the Biot-Savart law. For a small disc, the magnetic field dB can be expressed as:
dB=μ02⋅dIR
where dI is the differential current.
The differential current dI can be expressed in terms of the charge density:
dI=dQdt=QπR2⋅2πr⋅f
where r is the radius from the center to the differential area.
Integrating dB from 0 to R:
B=∫R0dB=μ02⋅∫R0Q⋅ω2πR⋅2πrdr
This leads to:
B=μ0ωQ4πR
Now, we can find the ratio of the magnetic dipole moment to the magnetic field:
MB=QωR22μ0ωQ4πR
This simplifies to:
MB=2πR3μ0
Thus, the ratio of the magnetic dipole moment to the magnetic field at the center of the disc is:
MB=πR32μ0
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SCQ_TYPE5videos
MAGNETICS
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE1videos
MAGNETICS
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE1videos
MAGNETICS
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery59videos
MAGNETIC FIELD AND FORCES
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery1videos
MAGNETISM AND MATTER
Similar Questions
Find the electric field on the axis of a charged disc.
View SolutionA uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is
 View Solution
View SolutionCalculate the magnetic field at distance y from the centre of the axis of a disc of radius r and unifrom surface charge density σ, If the disc spins with angular velocity ω ?
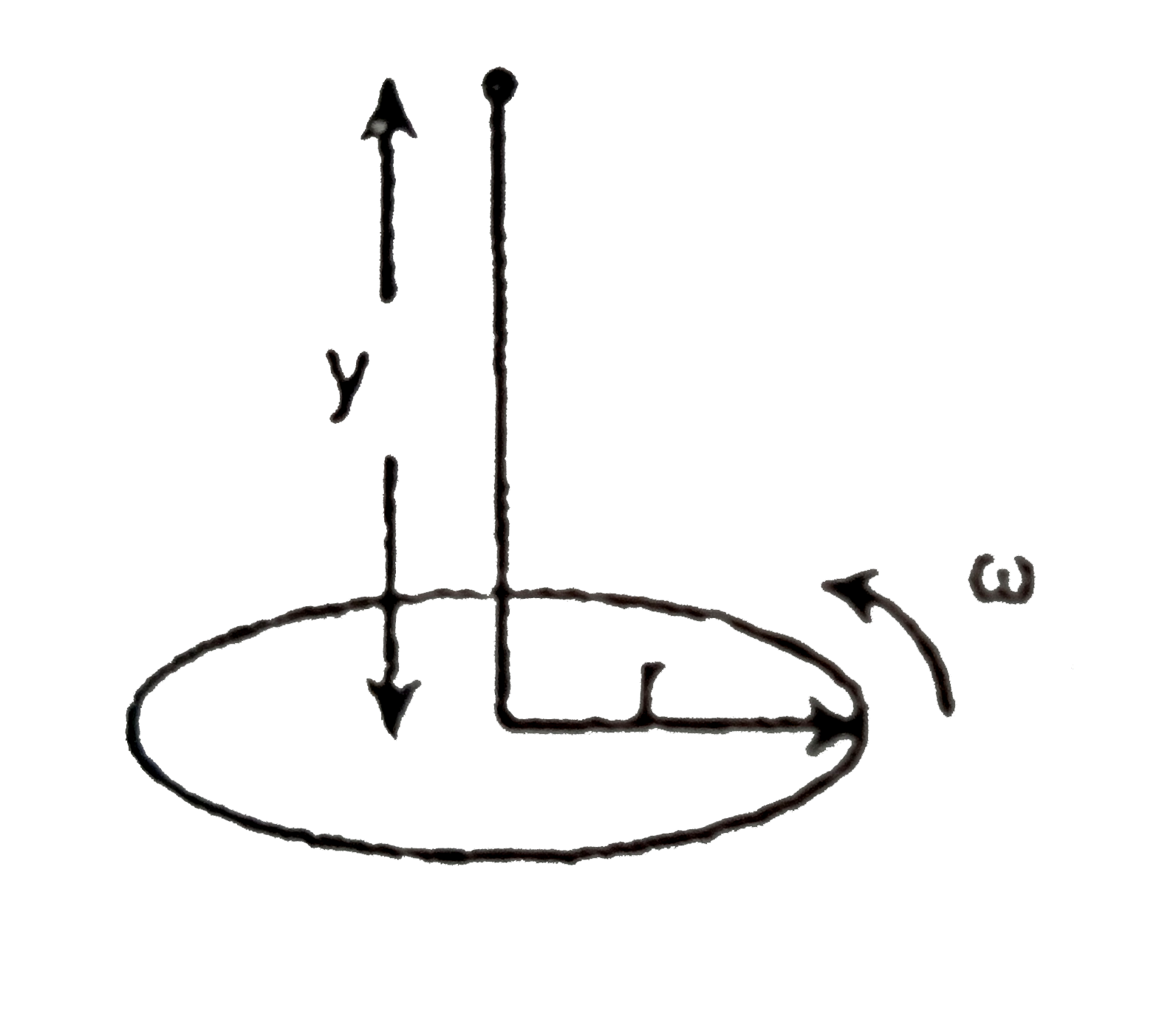 View Solution
View SolutionFind the position of instantaneous centre of rotation and angular velocity of the disc in the following cases as shown. Radius of disc is R in each case.
 View Solution
View SolutionMoment of inertia of a disc about an axis parallel to diameter and at a distance x from the centre of the disc is same as the moment of inertia of the disc about its centre axis. The radius of disc is R. The value of x is
View SolutionThe moment of inertia of a uniform circular disc of radius R and mass M about an axis passing from the edge of the disc and normal to the disc is.
View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.
 View Solution
View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.
 View Solution
View SolutionA disc of the moment of inertia 'l1' is rotating in horizontal plane about an axis passing through a centre and perpendicular to its plane with constant angular speed 'ω1' . Another disc of moment of inertia 'I2'. having zero angular speed is placed discs are rotating disc. Now, both the discs are rotating with constant angular speed 'ω2'. The energy lost by the initial rotating disc is
View SolutionA round disc of moment of inertia I2 about its axis perpendicular to its plane and passing through its centre is placed over another disc of moment of inertia I1 rotating with an angular velocity ω about the same axis. The final angular velocity of the combination of discs is.
View Solution

