Find the tension in the tape and the linear acceleration of the cylinder up the incline, assuming there is no slipping. (TakeM=4m and g=10m/s2)
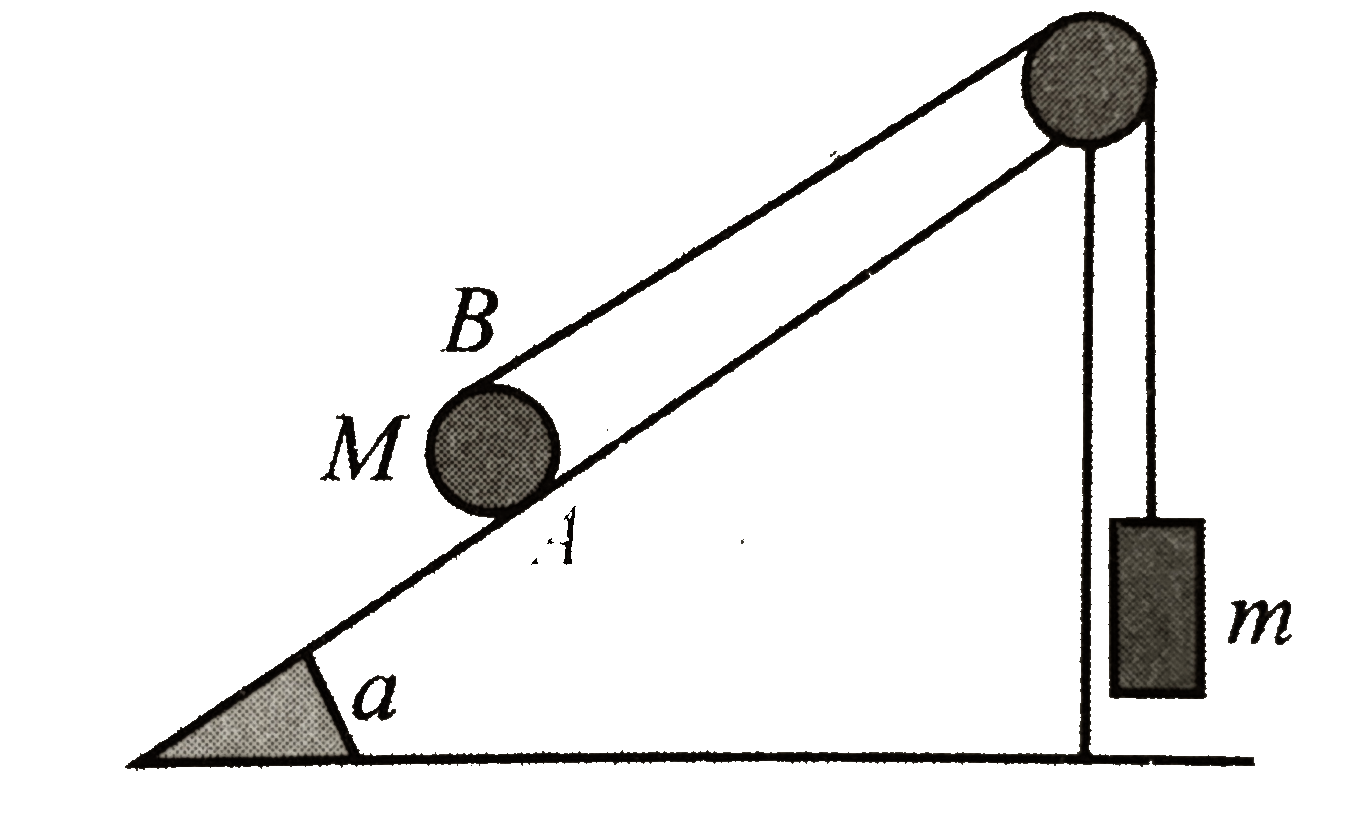
Since the cylinder does not slip, the displacement, velocity and acceleration of the hanging mass are, respectively, equal to the displacement, velocity and acceleration of the upper point B of the cylinder as the string leaves the upper point tangentially,
Now v(velocity of the upper point) =vm=ωr=2vCM
(∴ωr=vm)
From conservation of energy, when m lowers through h
mgh=12mv2+(12mv2CM+12Iω2)
( ∴ loss in PE= gain i KE)
=12mv2+12MV24+12(12Mr2)v2CMr2
(∴I=12Mr2)
(∵I=12Mr2)
=12mv2+18MV2+14Mv24
=12mv2+316Mv2
16mgh=8mv2+3Mv2
⇒v2=16mg8m+3M
From v2=2ah
⇒a=8mg8m+3M=g1+3M/8m=4m/s2
Considering downwardd motion m
mg−T=ma
or T=mg−ma=2(10−4)=12N
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Exercise 3.4
Explore 13 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Subjective
Explore 19 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Exercise 3.2
Explore 13 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICSChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
Similar Questions
A solid cylinder of mass M and radius R has a light thin tape wound around it as shown in the figure. The tape passes over a light, smooth fixed pulley to a block of mass m. Find the linear acceleration of the cylinder's axis up the incline (in) assuming no slipping. Given mass of the block = 1.5Kg, mass of the cylinder = 2 kg, the angle inclination = 30° and take g=10ms−2
View SolutionA solid cylinder of weight 20 kg and radius 7.5 cm is placed on a inclined plane with inclination 30∘ to the horizontal. A light thin tape is wound around the cylinder and is taken tangentially over the upper surface parallel to the plane and finally attached to a 5-kg body after passing over a light smooth pulley. Find the tension in the tape and linear acceleration of the cylinder up the plance, assuming no slip.
View SolutionA plank of mass M, is placed on a smooth surface over which a cylinder of mas m(=M) annd radius R=1m is placed as shown in figure. Now the plane is pulled towards the right wilth an external force F(=2Mg). If the cyinder does not slip over the surfcace of the plank, find the linear acceleration of he plank and the cylinder and the angular acceleration of the cylinder. (Take g=10ms2)

View SolutionFind the tensions in the two cords and the accelerations of the blocks in figure-2.22 if friction is negligible. The pulleys are massless and frictionless, m1=200gm,m2=500gm and m3=400gm, Take g=10m/s2.
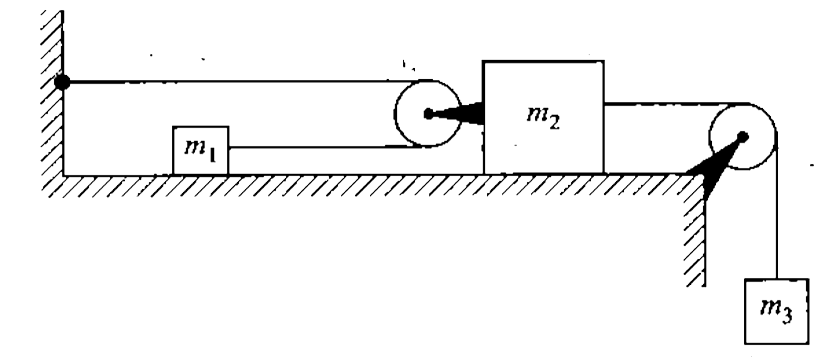
[0.94N,3.06N,4.7m/s2,2.35m/s2,2.35m/s2]
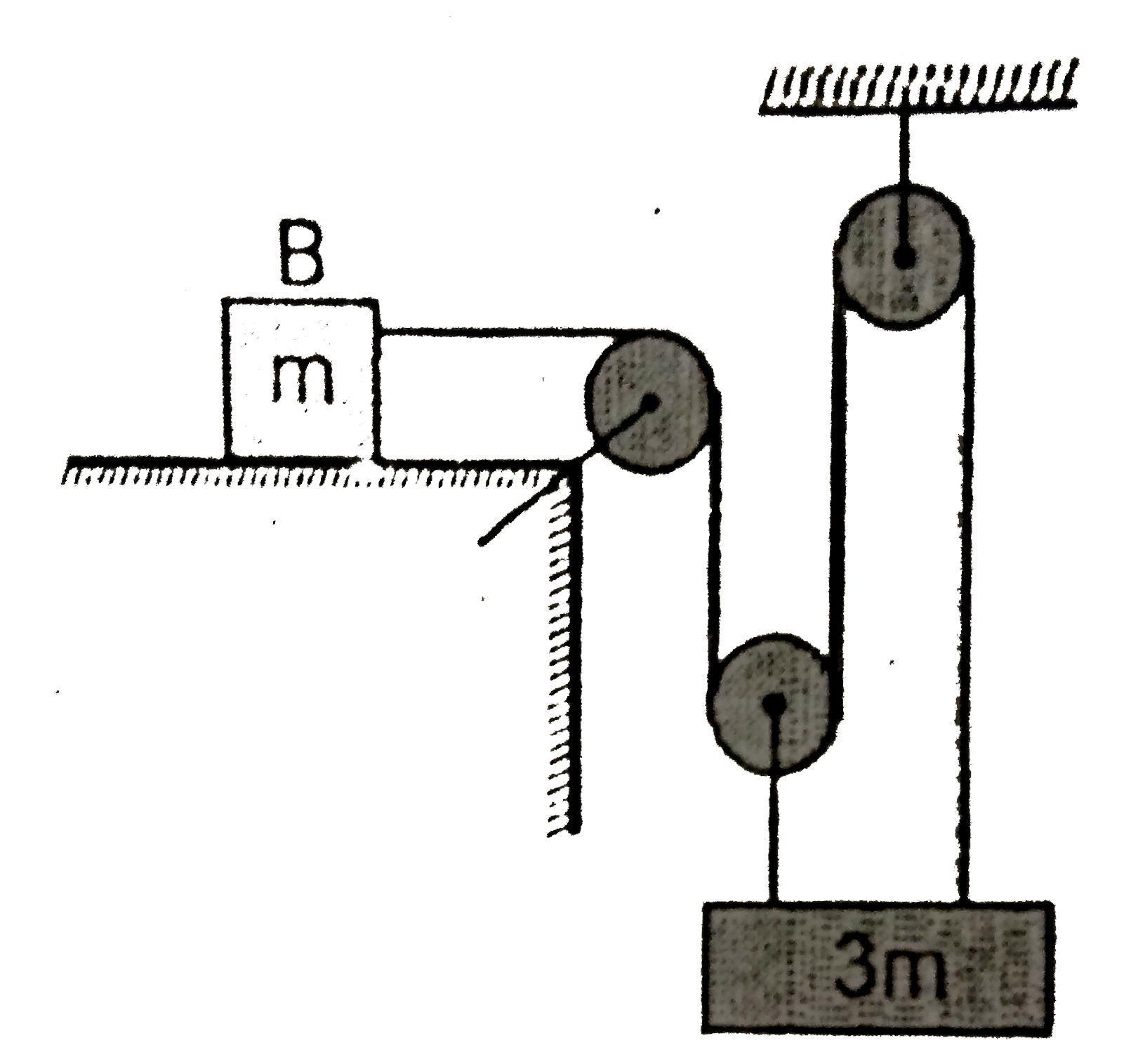
View SolutionIf the acceleration of the block B in the following system is a ( in m/s2) then find out value of 2a/5(g=10m/s2):
View SolutionIf coeffiecient of friction between the block of mass 2kg and table is 0.4 then out acceleration of the system and tension in the string. (g=10m/s2)
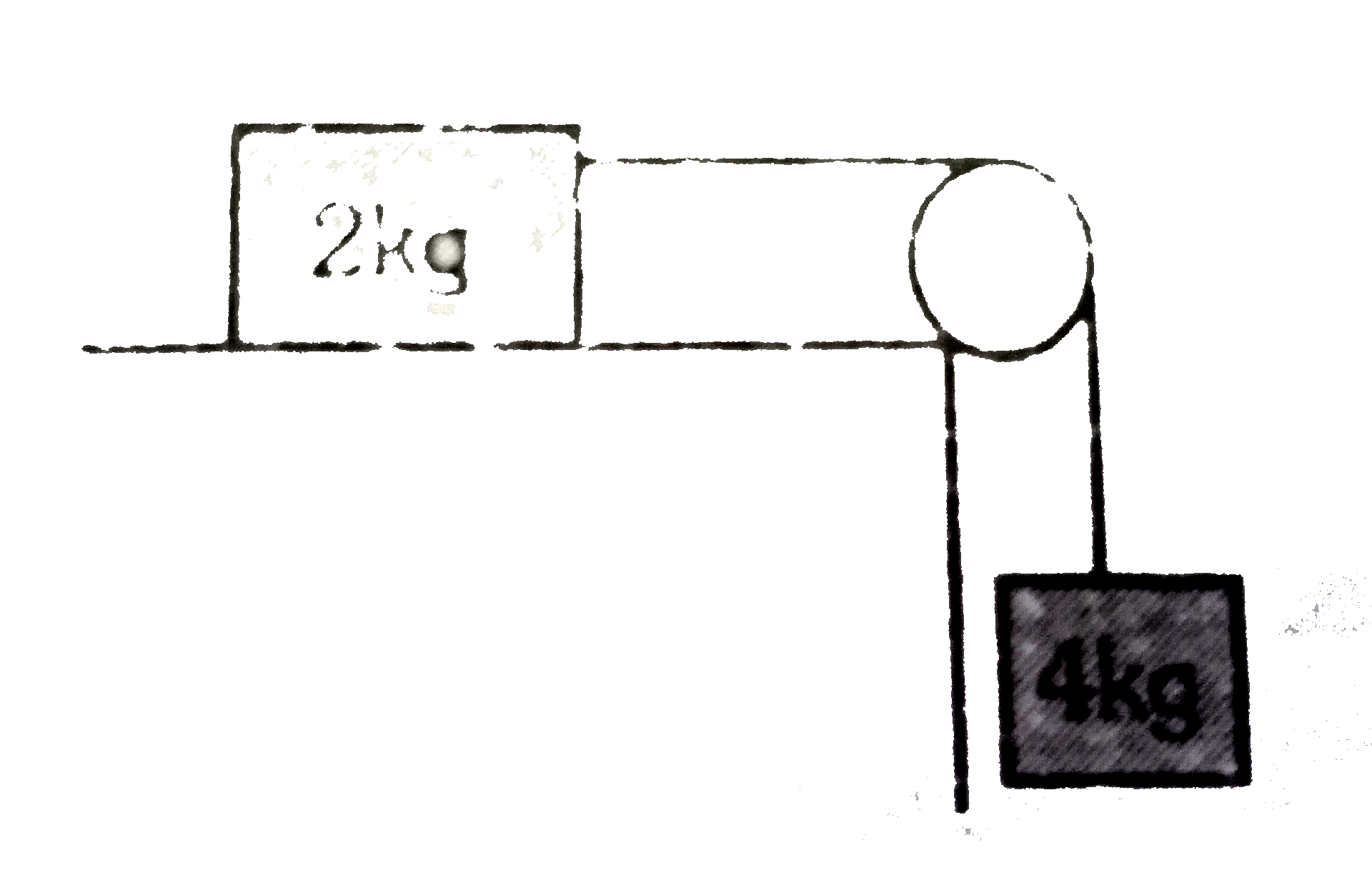
View SolutionA cylinder is released from the top of an incline making angle θ=45∘ with the horizontal. The length of the incline is 2.82m and mass of cylinder is 1kg. The coefficient of friciton is 0.2 between the cylinder and the incline. When the cylinder reaches the bottom of the incline, its total kinetic energy is (g=10m/s2)
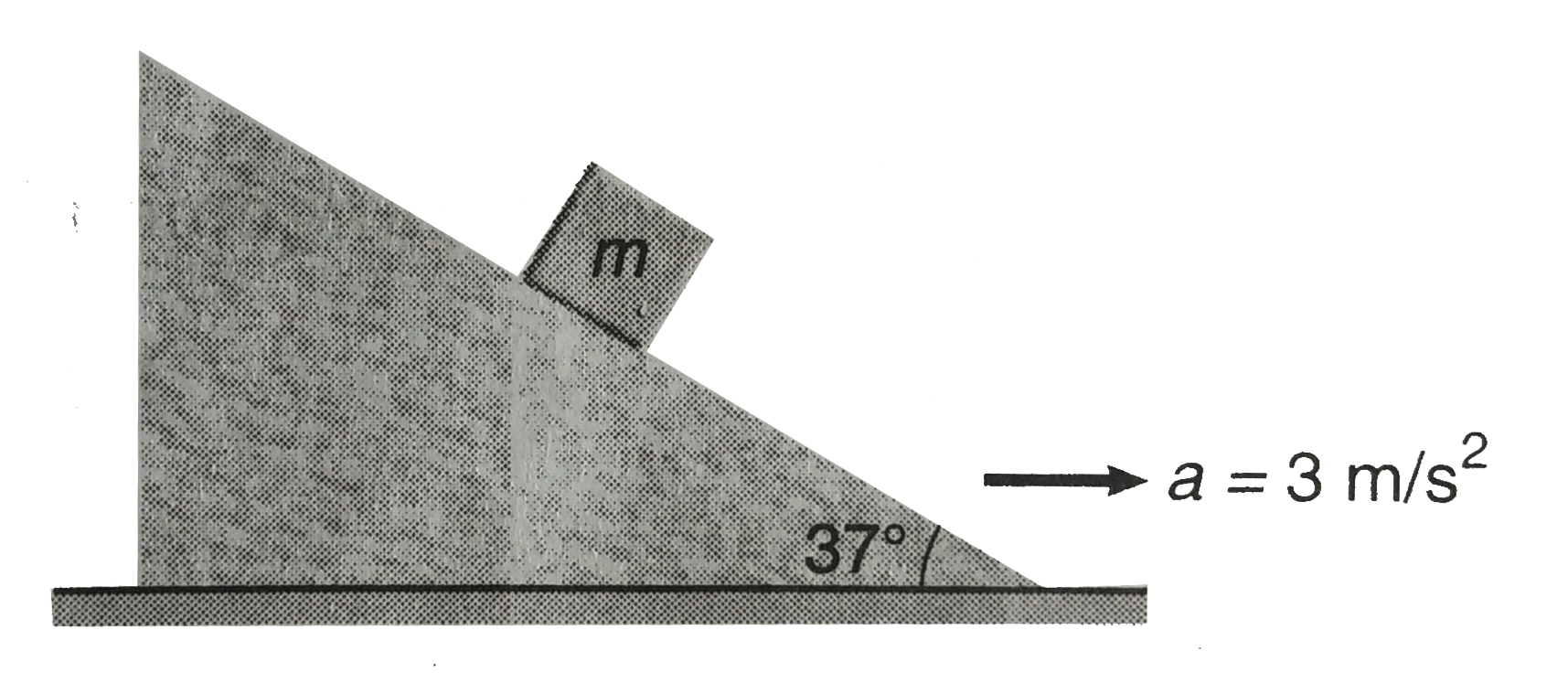
View SolutionA block is placed on an inclined plane as shown in figure. What must be the friction force between block and inclined if the block is not to slice along the inclined when the incline is accelerating to the right at 3m/s2(sin37∘=35)? (Takeg=10m/s2)
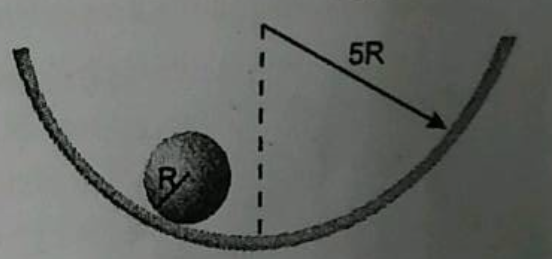
View SolutionA solid sphere of (radius =R) rolls without slipping in a cylindrical vessel (radius =5R). Find the time period of small of oscillations of the sphere in s−1. Take R=114m and g=10m/s2. (axis is cylinder is fixed and horizontal).
View SolutionCalculate the velocity with which a solid cylinder rolls down an inclined plane of height 10m with slipping (take g=10m/s2)
View Solution