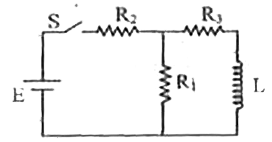
For the ciruit shown in figure E=50V, R1=10Ω,R2=20Ω,R3=30Ω and L=2.0mH. Find
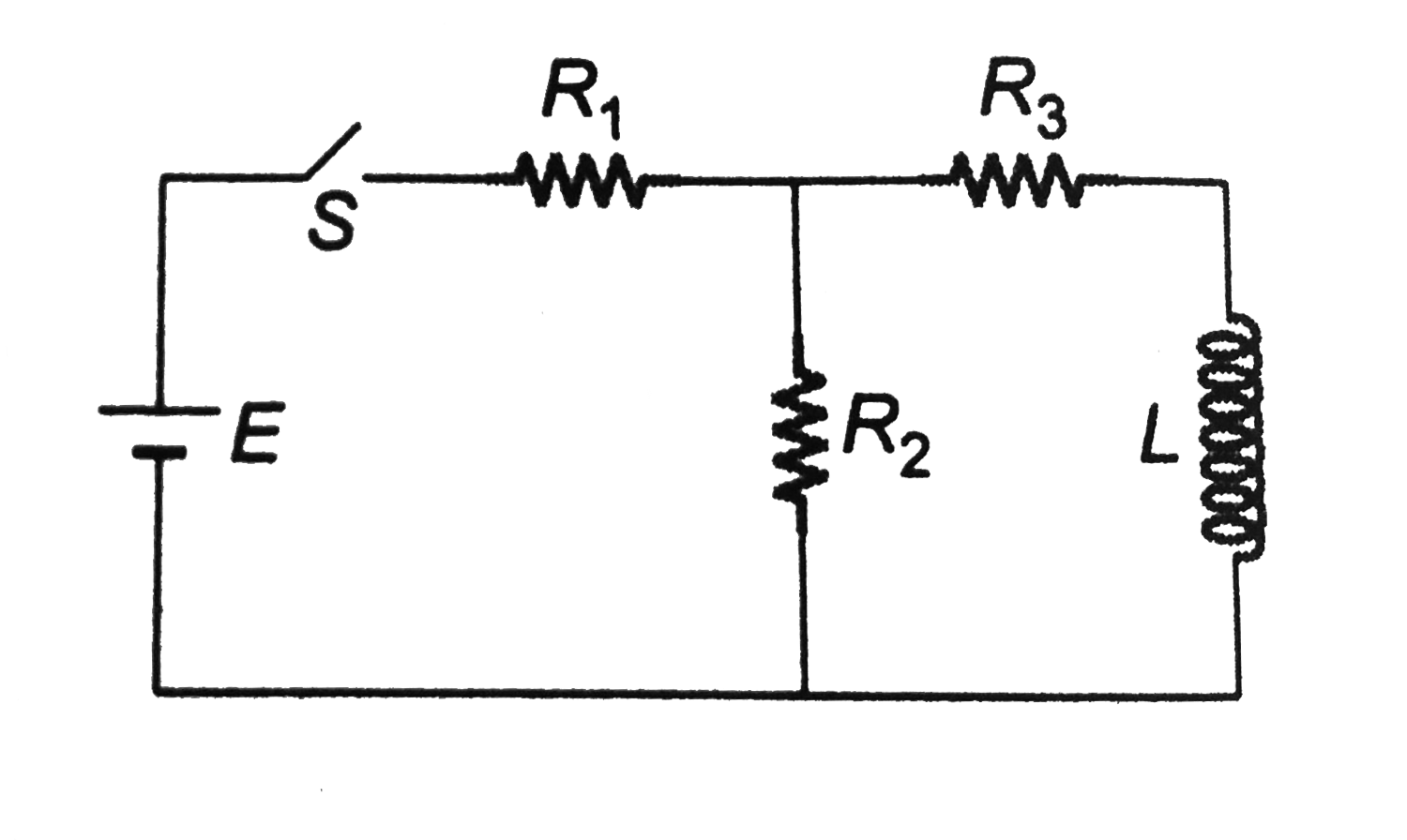
a. Immediately after switch S is closed
b. A long time after S is closed.
c. Immediaately after S is reopened
d. A long time after S is reopened.
a. Resistance offered by inductor immediately after switch is closed will be infinite.
Therefore current through R3 will be zero and
current through R1= current through R2=ER1+R2
=5010+20=53A
b. After long time of closing the switch, resistance offered by inductor will be zero.
In that case R2 and R3 are in parallel, and the resultant of these two is then in series with R1. Hence
Rnet=R1+R2R3R2+R3
=10+(20)(30)20+30=22Ω
Current though the battery (for thorugh R1)
ERnet=5022A
This current will distribute in R2 and R3 in invedrse ratio of resistance. Hence
Current through R2=(5022)(R3R2+R3)
=(5022)(2030+20)=1511A
c. Immediately after switch is reopened, the current through R1 will become zero.
But current thorgh R2 will be eqwual to the steady state current through R3, which is equal to
(5022−1511)A=0.91
d. A long after S is reopened, current through all resistors will be zero.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 4
2 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 5
2 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 2
2 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
In figure,ξ=100V,R1=10Ω,R2=20Ω,R3=30Ω and L=2H. Find i1&i2
(a)imeediately after switch Sw is closed
(b)a long time after
( c)immediately after Sw is opended again
(d)a long time later.
View SolutionFind the values of i1 and i2
(i) immediately after the switch S is closed.
(ii) long time later, with S closed.
(iii) immediately after S is open.
(iv) long time after S is opned.
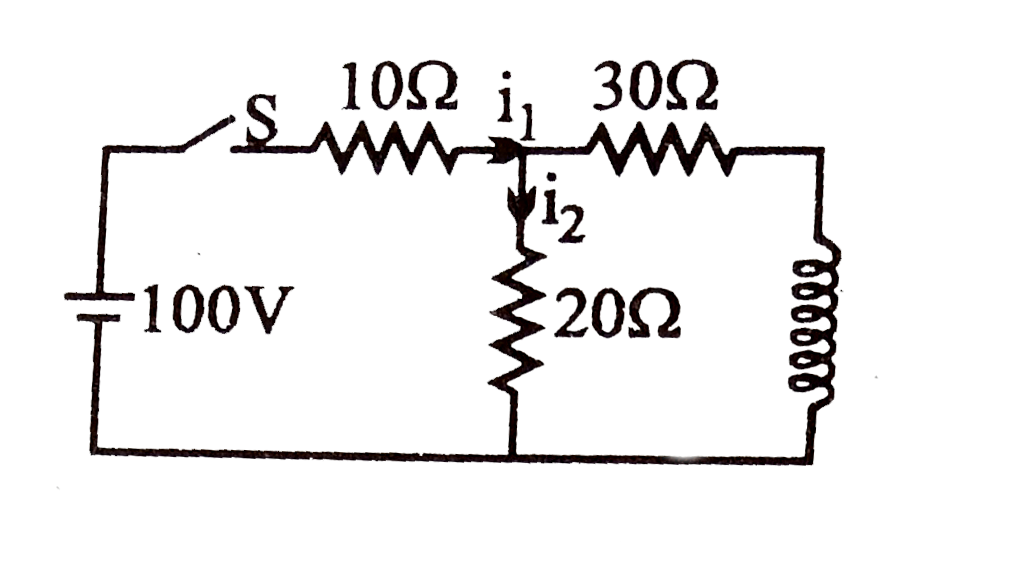
View Solution
Knowledge Check
In the circuit shown in adjoining fig E =10V, R1=1ΩR2=2Ω,R3=3ΩandL=2H. Calculate the value of current i1,i2andi3 immidiately after key S is closed :-
 A3.3 amp, 3.3 amp, 3.3 ampB3.3 amp, 3.3 amp, 0 ampC3.3 amp, 0 amp, 0 ampD3.3 amp , 3.3 amp 1.1 amp
A3.3 amp, 3.3 amp, 3.3 ampB3.3 amp, 3.3 amp, 0 ampC3.3 amp, 0 amp, 0 ampD3.3 amp , 3.3 amp 1.1 ampIn the circuit as shown in figure the switch is closed at t=0.

A long time after closing the switchAvoltage drop across the capacitor is EBcurent through the battery is E/R1+R2Cenegru stores in the capacitor is
12C(R2ER1+R2)2Dcurrent through the capacitor becomes zero
For the circuit shown E=50 V R1=10Ω,R2=20Ω,R3=30Ω L = 2.0 mH . The current through R1 and R2 are ________ . And _______ immediate after the switch is closed.
View SolutionIn the circuits show ε=15V,R1=1Ω,R2=1Ω,R3=2ΩandL=15H . Find the current i1,i2,i3 (i) immediately after the switch is closed (ii) immediately after the opening from the closed position (iii) sufficiently long after , the switch is opened f rom the colsed position,
View SolutionIn the circuit shown in the figure R1=R2=5Ω,C1=C2=2μfandε1=ε2=5V. Switch S1 is kept closed for a long time. Now switch S2 is also closed. Immediately after S1 is closed, find
(a) current through R1
(b) current through R2

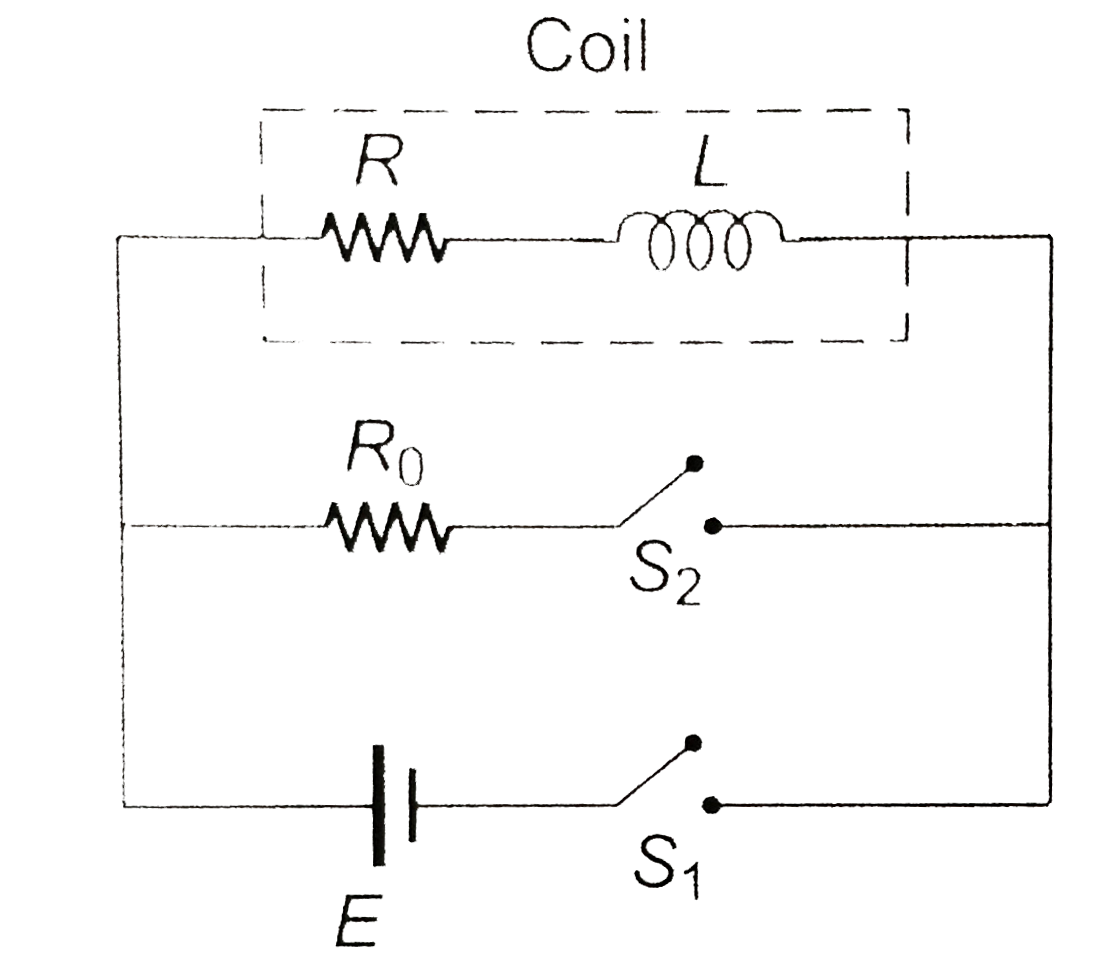
View SolutionInitally switch S1 is closed, after a long time, S1 is opened and S2 is closed. Find the heat produced in coil after long time.
View SolutionIn the circuit shown in figure, E=120V,R1=30.0Ω,R2=50.0Ω and L=0.200H. Switch S is closed at t=0. Just after the switch is closed.
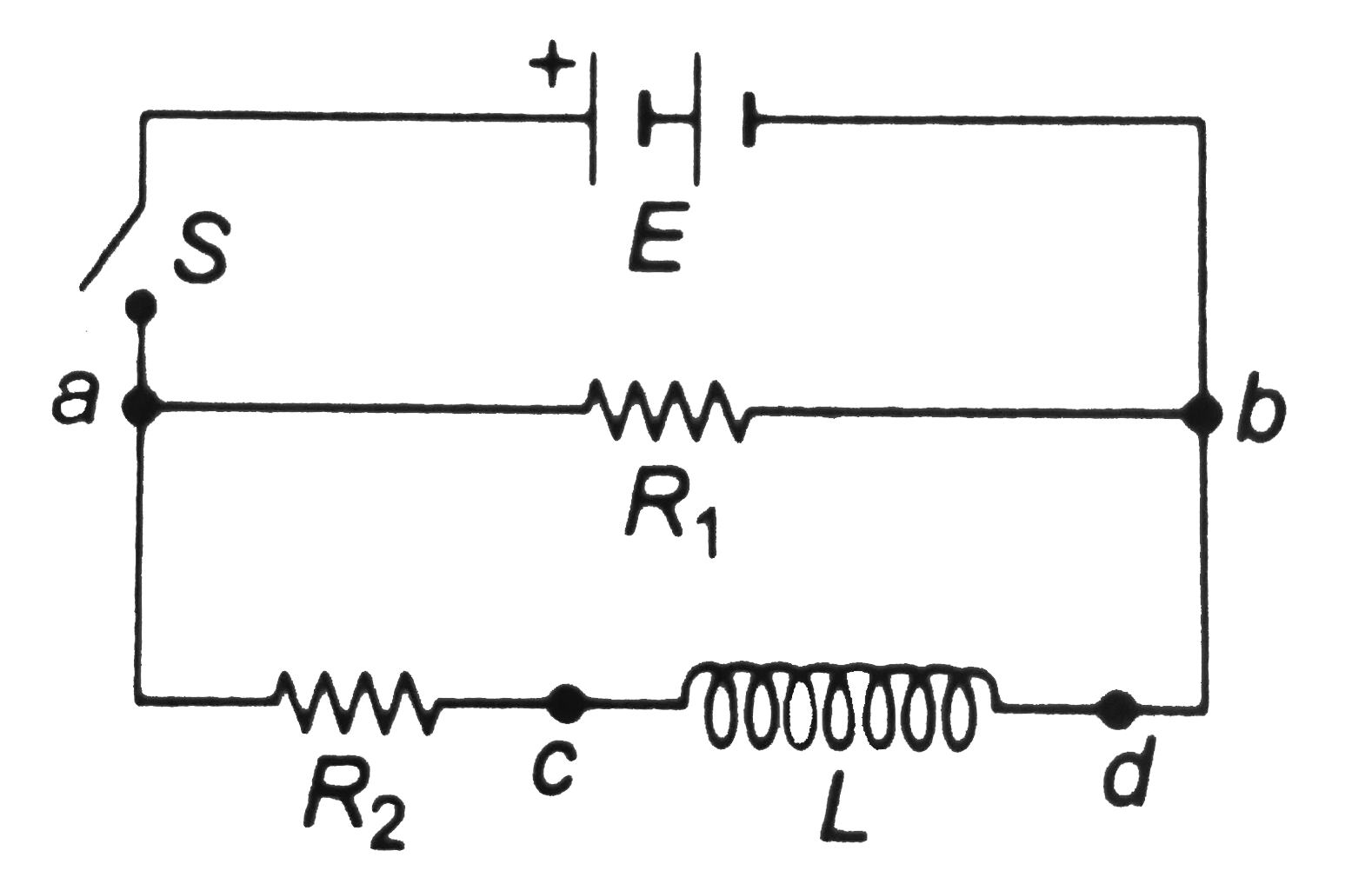
(a) What is the potential difference Vab across the inductor R1?
(b) Which point, a or b, is at higher potential?
(c) What is the potential difference Vcd across the inductor L?
(d) Which point, c or d, is at a higher potential? The switch is left closed for a long time and then is opened. Just after the switch is opened
(e) What is the potential difference Vab across the resistor R1?
(f) Which point a or b, is at a higher potential?
(g) What is the potential difference Vcd across the inductor L?
(h) Which point, c or d, is at a higher potential?
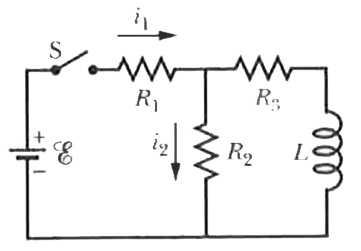
View SolutionIn Fig. 30-41, E = 100 V, R1=10.0Ω,R2=20.0Ω,R3=31.0Ω , and L = 2.00 H. Immediately after switch S is closed, what are (a) i1 and (b) i2? (Let currents in the indicated directions have positive values and currents in the opposite directions have negative values.) A long time later, what are (c) i1 and (d) i2? The switch is then reopened. Just then, what are (e) i1 and (f) i2? A long time later, what are (g) i1 and (h) i2?
View Solution
