For the uniform T shaped structure, with mass 3M, moment of inertia about an axis normal to the plane and passing through O would be
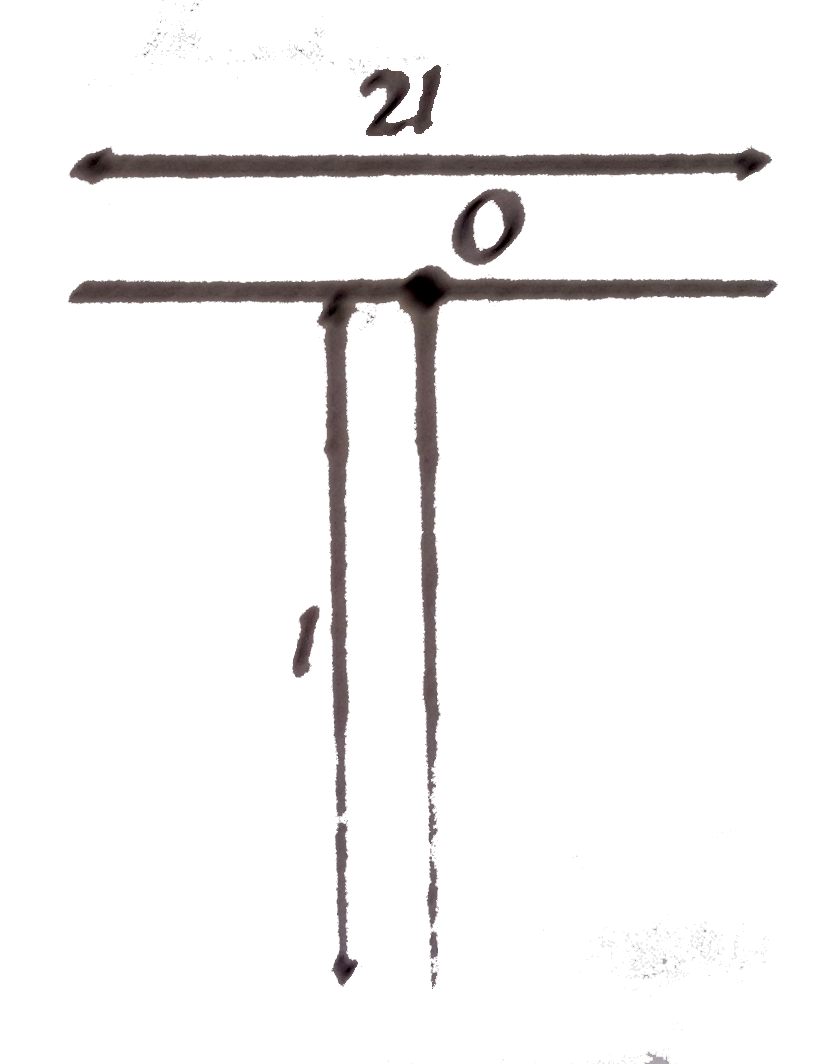
23Ml2
Ml2
Ml23
None of these
The correct Answer is:B
Moment of inertia, I=3[Ml23]=Ml2
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (B) Chapter Exercises
25 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - Check point 9.3
15 Videos
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - Integer type q.
15 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
Knowledge Check
Consider a uniform square plate of of side and mass m. The moment of inertia of this plate about an axis perpendicular to its plane and passing through one of its corners is -
A56ma2B112ma2C712ma2D23ma2Consider a uniform square plate of side 'a' and mass 'm'. The moment of inertia of this plate about an axis perpendicular to its plane and passing through one of its corners is
A112ma2B712ma2C23ma2D56ma2If I moment of inertia of a thin circular plate about an axis passing through tangent of plate in its plane. The moment of inertia of same circular plate about an axis perpendicular to its plane and passing through its centre is
A4I5B2I5C4I3D2I3
For the structure shown in figure, moment of inertia about an axis passing through yy' is
_PHY_213_Q01.png)
View SolutionFor the structure shown in figure, moment of inertia about an Axis passing through yy' is
_PHY_E05_238_Q01.png)
View Solution(i) Consider an infinitesimally thin triangular strip having mass M and length L. Find the moment of inertia of the strip about on axis passing through its tip and perpendicular to the plane. Compare the result with moment of inertia of a uniform disc of mass M and radius L about an axis passing through its centre and perpendicular to the plane the disc. Why the two expressions are same?

(ii) A circular fan made of paper is in shape of a disc of radius R. The fan can be folded (various stages shown in figure (a) through (f)) to the shape of a thin stick. The moment of inertia of the circular fan about an axis passing through centre O and perpendicular to the plane of the figure is I0=12MR2 where M= mass of the fan.

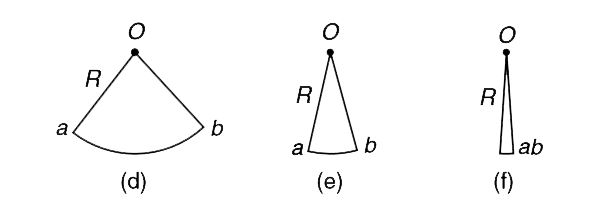
(a) How does the moment of inertia (I), about an axis perpendicular to the plane of the figure passing through O, change as the fan is folded through stage a to b to c to d to e?
(b) When the fan is completely folded in the shape of a stick (fig. (f)), write its moment of inertia about the above mentioned axis.
Note : Moment of inertia of a uniform rod about an axis through its end and perpendicular to it is ML23
View SolutionMoment of inertia of a half ring of mass m and radius R about an axis passing through point A perpendicular to the plane of the paper is IA. If IC is the moment of inertia of the ring about an axis perpendicular to the plane of paper and passing through point C, then

View SolutionMoment of inertia of a half ring of mass m and radius R about an axis passing through point A perpendicular to the plane of the paper is IA. If IC is the moment of inertia of the ring about an axis perpendicular to the plane of paper and passing through point C, then

View Solution
