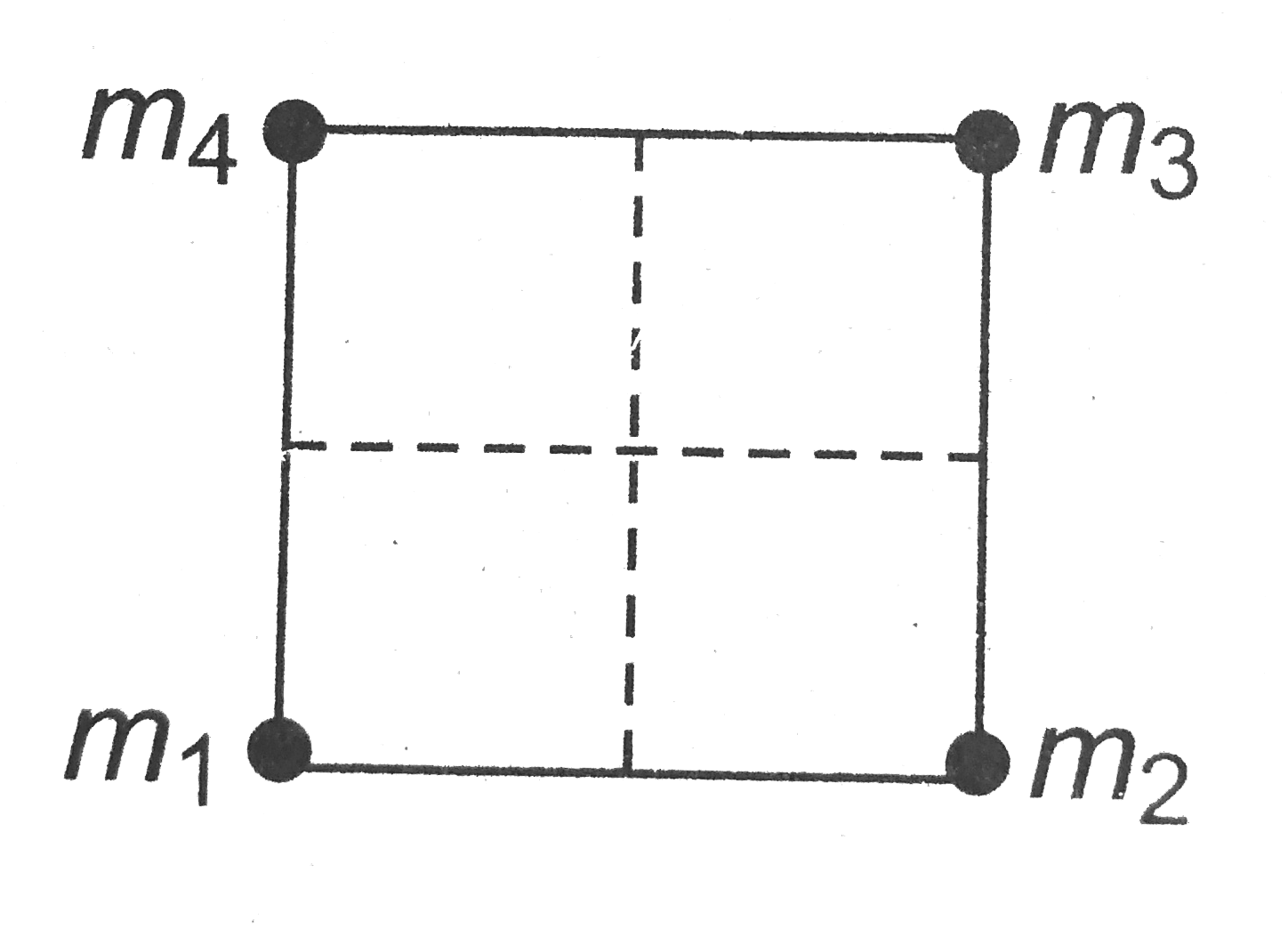
Four particles of masses m1=2m,m2=4m,m3=m and m4 are placed at four corners of a square . What should be the value of m4 , so that the centre of mass of all the four particles are exactly at the centre of the square ?

2m
8m
6m
None of these
The correct Answer is:D
xCM=0

or m1x1+m2x2+m3x3m1+m2+m3+m4=0
or (2m)(−a)+(4m)(a)+m(a)+m4(−a)=0
or m4=3m
Similarly yCM=0
or (2m)(−a)+4m(−a)+m(a)+m4(a)=0, or m94)=5m
Since, value of m4 are differeent to satisfy by both xCM=0 and yCM=0
Hence, it is not possible
Topper's Solved these Questions
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Taking it together
73 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion and reason
21 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
Similar Questions
Four paticle of masses m1=2m,m2=4m,m3=mandm4 are placed at four corners of a square. What should be the value of m4 so that the centres of mass of all the four particle are exactly at the centre of the square ?
View SolutionFour particles having masses, m, 2m, 3m, and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the centre.
View SolutionFour particles having masses, m, 2m, 3m, and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the centre.
View SolutionFour particles having masses, m, 2m, 3m, and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the center.
View SolutionIf four different masses m1,m2,m3 and m4 are placed at the four corners of a square of side a, the resultant gravitational force on a mass m kept at the centre is
View SolutionThree point masses m1=2Kg,m2=4kgandm3=6kg are kept at the three corners of an equilateral triangle of side 1 m. Find the locationo of their center of mass.
View SolutionFour point are placed at four comerse of a squared of side 4 m as shown. Match the following table.

View SolutionFour particles of masses m,2m,3m,4m are placed at corners of a square of side 'a' as shown in fig. Find out coordinateds of centre of mass.
View SolutionFour point masses are plaaced at four corners of a square as shows. When positions of mand 2m are interchanged

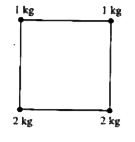
View SolutionFour point masses 1 kg, 1 kg, 2 kg and 2 kg are placed at the corners of a square of side a m as shown in Fig. Find the centre of mass of the system.
View Solution
