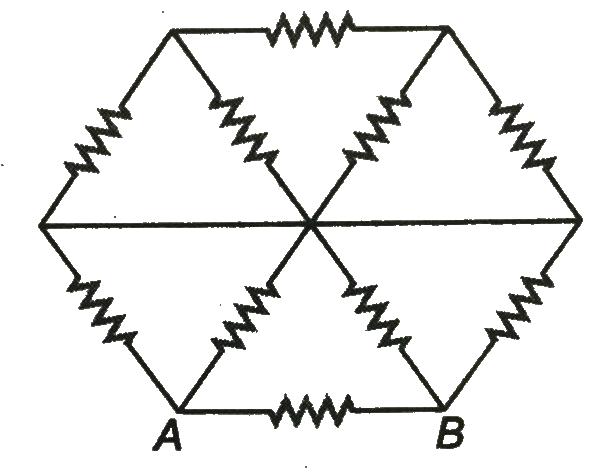
Four resistances of 2.0 Ω each are joined end to end, to form a square ABCD. Calculate the equivalent resistance of the combination between any two adjacent corners
To find the equivalent resistance between two adjacent corners (A and B) of a square formed by four resistances of 2.0 ohms each, we can follow these steps:
Step 1: Identify the Configuration
We have a square ABCD with each side having a resistance of 2.0 ohms. The resistances can be labeled as follows:
- R1 (AB) = 2.0 ohms
- R2 (BC) = 2.0 ohms
- R3 (CD) = 2.0 ohms
- R4 (DA) = 2.0 ohms
Step 2: Analyze the Circuit
To find the equivalent resistance between points A and B, we can observe that:
- The resistance R1 (AB) is directly between points A and B.
- The other two resistances (R2 and R4) are connected to points B and A respectively, forming a path through points C and D.
Step 3: Calculate the Series Resistance
The resistances R2 (BC) and R4 (DA) are in series with each other when considering the path from A to B through C and D. Thus, we can calculate the total resistance of this series path:
- R_series = R2 + R4 = 2.0 ohms + 2.0 ohms = 4.0 ohms
Step 4: Set Up the Parallel Resistance Calculation
Now, we have:
- R1 (the direct path from A to B) = 2.0 ohms
- R_series (the indirect path from A to B through C and D) = 4.0 ohms
Since R1 and R_series are in parallel, we can use the formula for equivalent resistance in parallel:
1RAB=1R1+1Rseries
Substituting the values:
1RAB=12.0+14.0
Step 5: Calculate the Equivalent Resistance
Now, we simplify the equation:
1RAB=12+14=24+14=34
Thus,
RAB=43 ohms≈1.33 ohms
Step 6: Final Calculation
Therefore, the equivalent resistance between any two adjacent corners (A and B) of the square is:
RAB=1.33 ohms
We have a square ABCD with each side having a resistance of 2.0 ohms. The resistances can be labeled as follows:
- R1 (AB) = 2.0 ohms
- R2 (BC) = 2.0 ohms
- R3 (CD) = 2.0 ohms
- R4 (DA) = 2.0 ohms
To find the equivalent resistance between points A and B, we can observe that:
- The resistance R1 (AB) is directly between points A and B.
- The other two resistances (R2 and R4) are connected to points B and A respectively, forming a path through points C and D.
The resistances R2 (BC) and R4 (DA) are in series with each other when considering the path from A to B through C and D. Thus, we can calculate the total resistance of this series path:
- R_series = R2 + R4 = 2.0 ohms + 2.0 ohms = 4.0 ohms
Now, we have:
- R1 (the direct path from A to B) = 2.0 ohms
- R_series (the indirect path from A to B through C and D) = 4.0 ohms
1RAB=1R1+1Rseries
Substituting the values:
1RAB=12.0+14.0
Now, we simplify the equation:
1RAB=12+14=24+14=34
Thus,
RAB=43 ohms≈1.33 ohms
Therefore, the equivalent resistance between any two adjacent corners (A and B) of the square is:
RAB=1.33 ohms
Topper's Solved these Questions
Similar Questions
Knowledge Check
Two resistances R1=100±3ΩandR2=200±4Ω are connected in series . Find the equivalent resistance of the series combination.
A(66.7±1.8)ΩB(66.7±4.0)ΩC(66.7±3.0)ΩD(66.7±7.0)Ω
The resistance of each side of an equilateral triangle is 6 ohm. Calculate the equivalent resistance between ends of a side.
View SolutionEight identical resistances reach are connected along edges of a pyramid having square base ABCD as shown. Calculate equivalent resistance between A and D.
View SolutionA wire of resistance 15.0(Ω)is bent to form a regular hexagon ABCDEFA.Find the equivalent resistance of the loop between the points (a)A and B, (b)A and C and (c )A and D .
View SolutionA metallic wire having a resistance of 20Ω is bent in order to form a complete circle. Calculate the resistance between any two diametrically opposite points on the circle.
View SolutionTwo resistances R1=100±3ΩandR2=200±4Ω are connected in series . Find the equivalent resistance of the series combination.
View SolutionFour wires of equal length and of resistance 5ohm each are connected in the form of a square. The equivalent resistance between the diagonally opposite corners of the square is
View Solution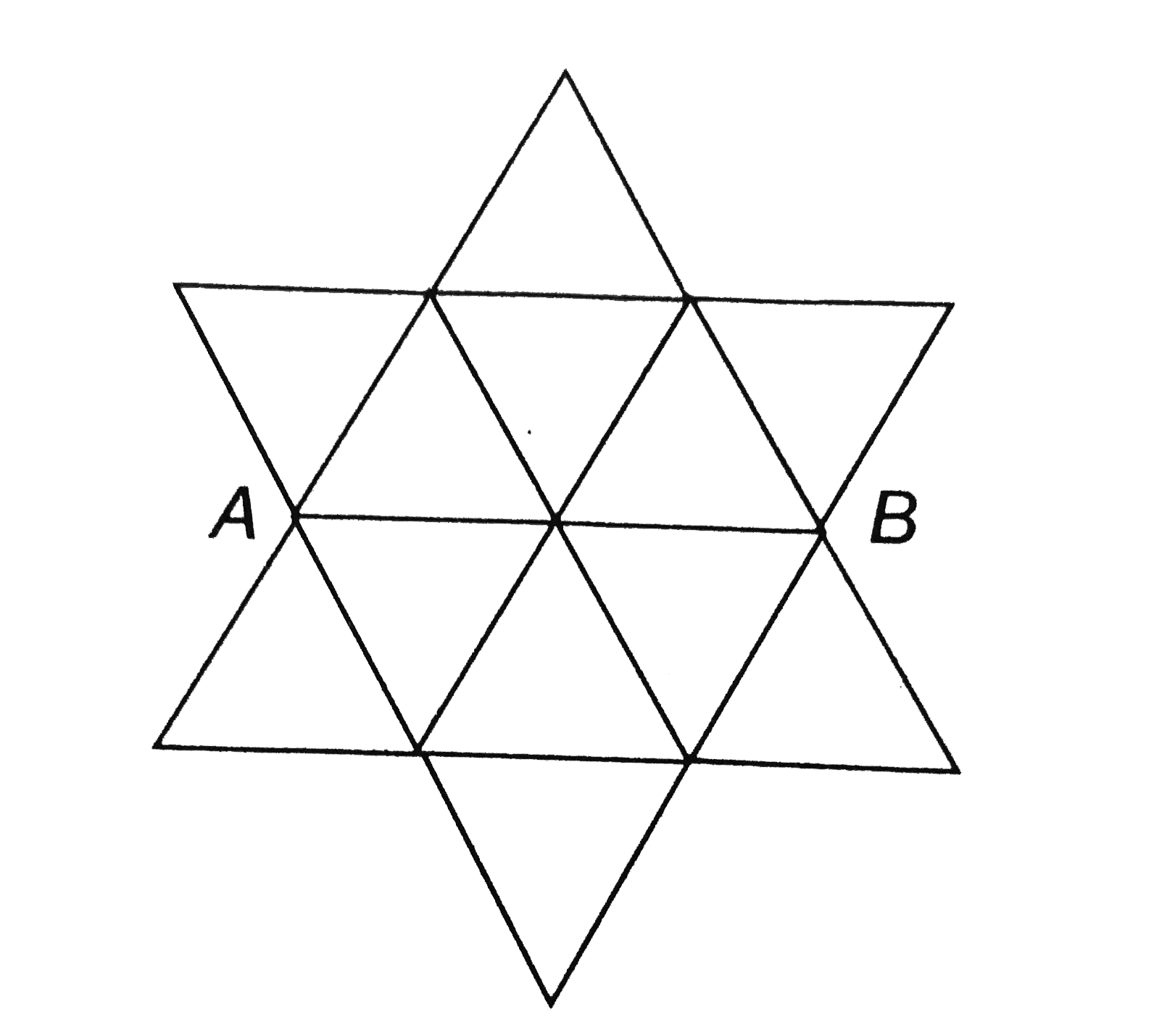
If the resistance of each branch of the circuit shown below is 1Ω , then the equivalent resistance of the circuit between the points A and B is
View Solution