From a massless string, a metallic cube of edge 3 cm is suspended and them immersed in water as shown in figure. If the density of metal is 5×103kg/m3 then find the tension in the string if the given system is
(a) at rest
(b) moving downwards with an acceleration of 3m/s2 .
(C) moving upwards with an acceleration of 3m/s2. 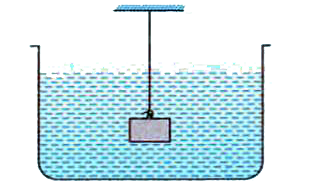
Density of cube (σ)=5×103kg/m3
Density of water (p)=103kg/m3
V=Volume of cube =3cm×3cm×3cm
=27cm3=27×10−6m3
W=Weight of cube =volume × density×g=Vσg
Weight of water displaced =upthrust =Vpg
Case (i): When system is at rest
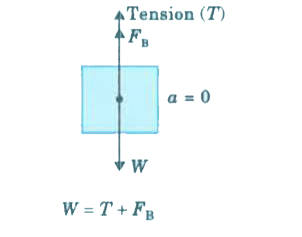
W=T+FB
T=W−FB
=Vσg−Vpg
=Vg(σ−p)
=27×10−6×10×(5000−1000)
=1.08 N
Case (ii) :System is moving downwards
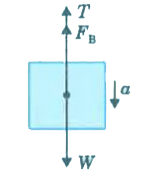
Effective value of acceleration =g.=g−a
T+FB=W
T=W−FB
=σVg.−pVg.
=Vg.(σ−p)
=V(g−a)(σ−p)
=27×10−6(10−3)(5000−1000)
=0.756 N
Case (iii): When system is moving upwards then g.=g+a
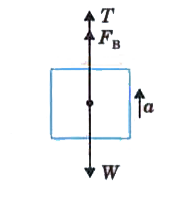
Effective value of g=g.=g+a
T=W−FB
=Vσg.−Vpg.
=Vg.(σ−p)
=27×10−6×(10+3)(5000−1000)
=1.40 N
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT (Textbook Exercises)
20 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT (Additional Exercises)
11 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Conceptual Questions
29 Videos
- MATHEMATICAL TOOLSBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)
12 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
Similar Questions
A solid cube of sides 2 cm each is suspended by a thread and completely immersed in a liquid of density 0.85×103 kg/m3. What will be the tension in the thread if relative density of solid is 5?
View SolutionA metal cube of 5cm side and relative density 9 is suspended by thread so as to be dompletely immersed in a liquid of density 1.2×103kgm−3. Find the tension in the thread.
View Solution
Knowledge Check
The R.D of a metal block is 2.7×103kg/m3. It is immersed in water. Then the block
AsinksBflotsCis partially immersedDhas no part immersedA lift of mass 100 kg is moving upwards with an acceleration of 1 m/s2. The tension developed in the string, which is connected to lift is (g=9.8m/s2)
A980 NB1080 NC1100 ND1000 NIf acceleration of block B is 4m/s2 upward & that of C is 6m/s2 downward. Find acceleration of A :−
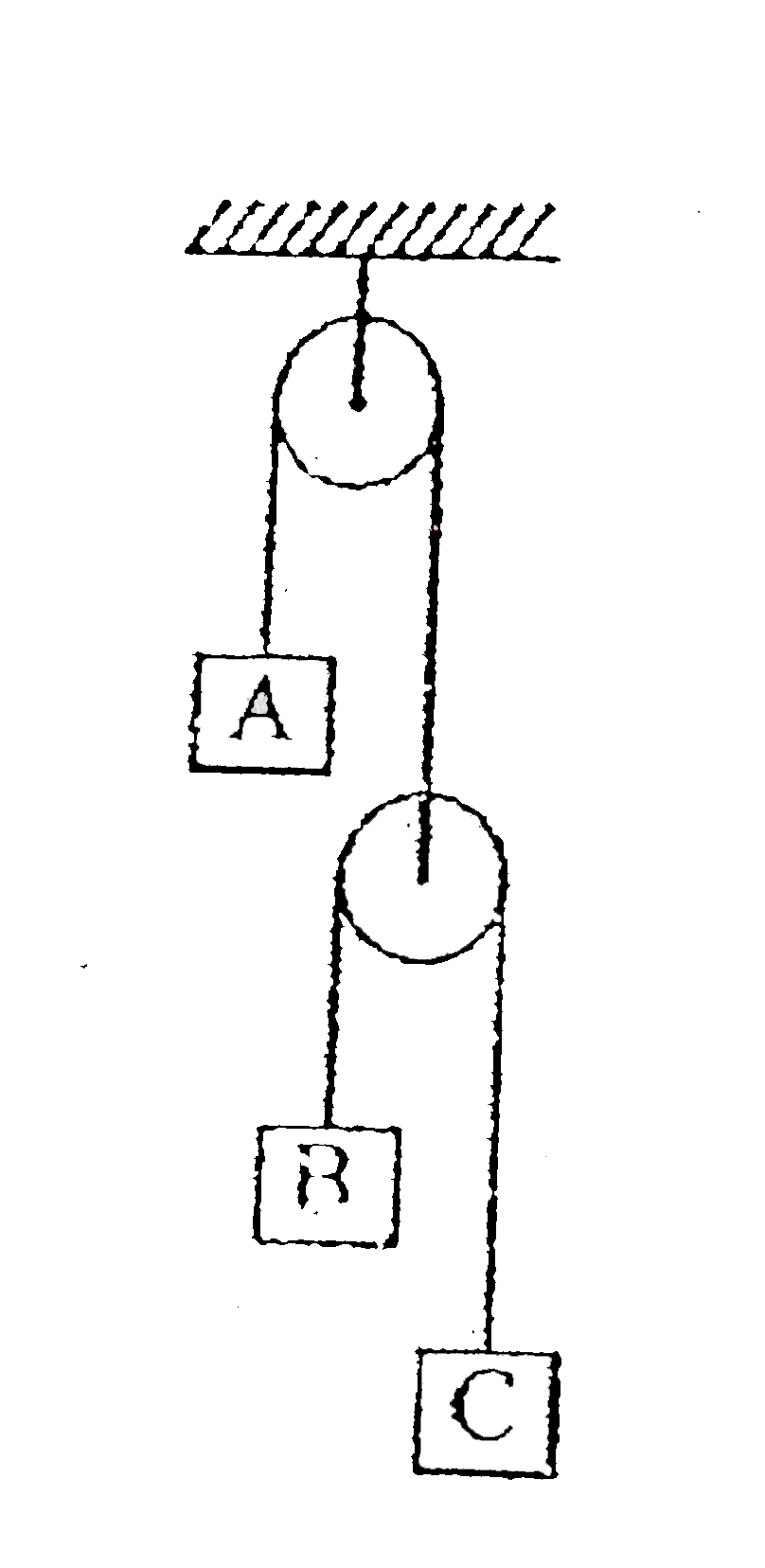 A2m/s2 upwardB1m/s2 upwardC1m/s2 downwardD2m/s2 downward
A2m/s2 upwardB1m/s2 upwardC1m/s2 downwardD2m/s2 downward
A 'block' of mass 10 kg is suspended with string as shown in figure. Find tension in the string. (g=10m/s2)

View SolutionIn the figure shown,a3=6m/s2 (downwards) and a3=6m/s2 (upwards) .Find acceleration of 1

View SolutionThe distance travelled by a particle starting from rest and moving with an acceleration 4/3m/s2 ,in the third-second is
View SolutionFigure shown a block of mass m placed on a smooth wedge of mass M. Calculate the minimum value of M' and tension in the string, so that the block of mass m will move vertically downwards with acceleration 10ms−2
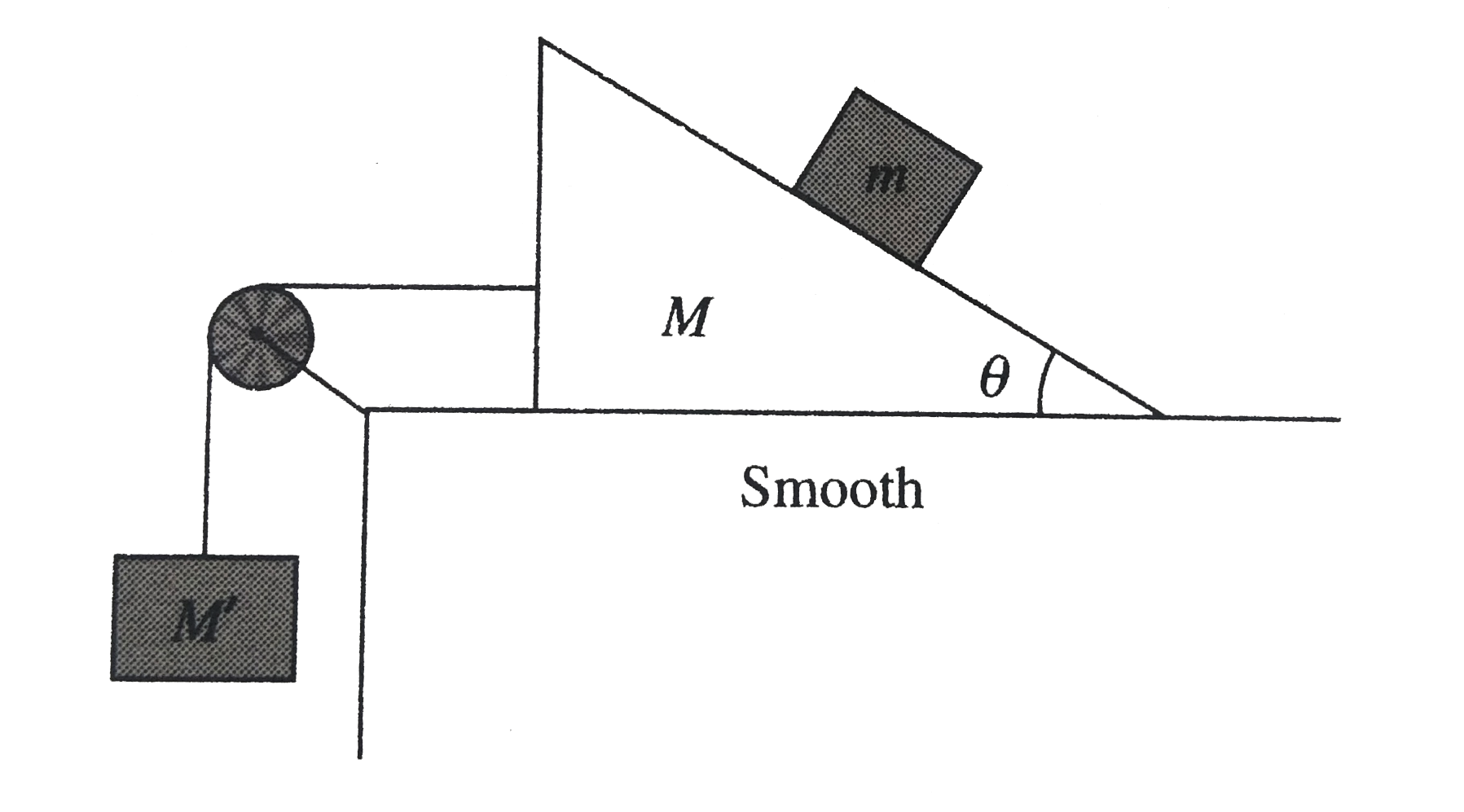
View SolutionA bob of pendulum of mass 50 g is suspended by string with the roof of an elevator. If the lift is flying with a uniform acceleration of 5ms−2 the tension in the string is (g=10ms−2)
View Solution
