From the velocity-time graph of uniformaccelerated motion deduce the equations of motion in (i) velocity and time (ii) distance and time (iii) disstance and velocity.
To deduce the equations of motion from the velocity-time graph of uniformly accelerated motion, we will derive three equations: (i) relating velocity and time, (ii) relating distance and time, and (iii) relating distance and velocity.
Step 1: Velocity-Time Relation
1. Understanding the Graph: In a velocity-time graph for uniformly accelerated motion, the graph is a straight line. Let the initial velocity be u and the final velocity be v, with time t taken to reach from u to v.
2. Finding the Slope: The slope of the velocity-time graph represents acceleration a. Mathematically, the slope can be expressed as:
a=v−ut
3. Rearranging the Equation: Rearranging the above equation gives:
v−u=at
Thus, we can express v as:
v=u+at
This is the first equation of motion.
Step 2: Distance-Time Relation
1. Understanding Distance: The distance s traveled can be found by calculating the area under the velocity-time graph.
2. Calculating Area: The area under the graph can be divided into a rectangle and a triangle:
- The rectangle has a base of t and height u, giving an area of ut.
- The triangle has a base of t and height v−u, giving an area of 12×t×(v−u).
3. Total Distance: Therefore, the total distance s is:
s=ut+12(v−u)t
4. Substituting for v: Using the first equation of motion v=u+at, we can substitute v−u with at:
s=ut+12att
This simplifies to:
s=ut+12at2
This is the second equation of motion.
Step 3: Distance-Velocity Relation
1. Eliminating Time: To find the relation between distance and velocity, we can eliminate time from the equations. We already have:
s=ut+12at2
and from the first equation of motion:
t=v−ua
2. Substituting for Time: Substitute t in the distance equation:
s=u(v−ua)+12a(v−ua)2
3. Simplifying the Equation: After simplification, we get:
s=u(v−u)a+12(v−u)2a
Combining the terms leads to:
s=(v−u)(u+12(v−u))a
This simplifies to:
s=(v2−u2)2a
This is the third equation of motion.
Summary of Equations of Motion
1. Velocity-Time Relation: v=u+at
2. Distance-Time Relation: s=ut+12at2
3. Distance-Velocity Relation: s=(v2−u2)2a
a=v−ut
v−u=at
Thus, we can express v as:
v=u+at
This is the first equation of motion.
- The rectangle has a base of t and height u, giving an area of ut.
- The triangle has a base of t and height v−u, giving an area of 12×t×(v−u).
s=ut+12(v−u)t
s=ut+12att
This simplifies to:
s=ut+12at2
This is the second equation of motion.
s=ut+12at2
and from the first equation of motion:
t=v−ua
s=u(v−ua)+12a(v−ua)2
s=u(v−u)a+12(v−u)2a
Combining the terms leads to:
s=(v−u)(u+12(v−u))a
This simplifies to:
s=(v2−u2)2a
This is the third equation of motion.
2. Distance-Time Relation: s=ut+12at2
3. Distance-Velocity Relation: s=(v2−u2)2a
Topper's Solved these Questions
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 3 Short answer
37 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 4 Short answer
30 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 Short answer
25 Videos
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - Assertion-Reason Type Questions
19 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Assertion- Reason Type Questions
17 Videos
Similar Questions
Represent the velocity-time graph for a uniformly accelerated motion when acceleration is positive.
View SolutionDraw velocity – time graph of uniformly accelerated motion in one dimension. From the velocity – time graph of uniform accelerated motion, deduce the equations of motion in distance and time.
View Solution
Knowledge Check
The slope of velocity-time graph for uniform motion of an object is
AUnityBZeroCInfiniteDMore than unity but has some finite valueThe velocity -time graph for a body with non-uniform motion is a
Astraight lineBstraight line parallel to x-axisCstraight line parallel to y-axisDcurved lineIn relation to a velocity-time graph
Athe curve can be a circleBthe area under the curve and above the time axis between any two instants gives the average acceleration.Cthe slope at any instant gives the rate of change of acceleration at that instantDthe area under the curve and above the time axis gives the displacement.
Draw the velocity-time graph for uniformly accelerated motion. Show that slope of the velocity-time graph gives acceleration of the object.
View SolutionWrite some uses of velocity-time graph of an object in uniform motion.
View SolutionThe velocity time graph of the motion of a car is given here.
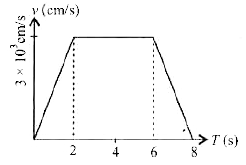
View SolutionThe velocity-time graph of particle comes out to be a non-linear curve. The motion is
View SolutionWhich of the following velocity-time graphs does not represent motion in one dimension?
View Solution
