If earth decreases its rotational speed. Match the following columns
Column-IColumn-II(A)Value of g at pole(p)Will remain same(B)Value of g at equator(q)Will increase(C)Distance of geostationary(r)Will decrease(D)Energy of geostationary satellite(s)Cannot say
The correct Answer is:(A→p,B→q,C→q,D→q)
To solve the problem, we need to analyze the effects of a decrease in the Earth's rotational speed on various parameters related to gravity and geostationary satellites. We will match the items in Column I with the correct statements in Column II.
1. Value of g at the Pole (A):
- At the poles, the only force acting is the gravitational force since the centrifugal force due to rotation is zero (as the rotational speed is zero).
- Therefore, the value of g at the pole remains constant regardless of changes in rotational speed.
- Match: (A) → (p) Will remain same.
2. Value of g at the Equator (B):
- At the equator, the effective value of g (g') is given by the equation:
g′=g−ω2R
where ω is the angular velocity and R is the radius of the Earth.
- If the rotational speed decreases (i.e., ω decreases), the term ω2R decreases, leading to an increase in the effective value of g at the equator.
- Match: (B) → (q) Will increase.
3. Distance of Geostationary Satellite (C):
- The orbital period T of a geostationary satellite is related to the angular velocity ω by:
T=2πω
- If ω decreases, T increases. According to Kepler's third law:
T2∝R3
If T increases, the distance R must also increase.
- Match: (C) → (r) Will decrease.
4. Energy of Geostationary Satellite (D):
- The gravitational potential energy E of a satellite is given by:
E=−GMmR
- As the distance R increases (from the previous step), the magnitude of the energy (which is negative) becomes less negative, indicating that the energy increases.
- Match: (D) → (s) Cannot say.
Final Matches:
- (A) → (p)
- (B) → (q)
- (C) → (r)
- (D) → (s)
- At the poles, the only force acting is the gravitational force since the centrifugal force due to rotation is zero (as the rotational speed is zero).
- Therefore, the value of g at the pole remains constant regardless of changes in rotational speed.
- Match: (A) → (p) Will remain same.
- At the equator, the effective value of g (g') is given by the equation:
g′=g−ω2R
where ω is the angular velocity and R is the radius of the Earth.
- If the rotational speed decreases (i.e., ω decreases), the term ω2R decreases, leading to an increase in the effective value of g at the equator.
- Match: (B) → (q) Will increase.
- The orbital period T of a geostationary satellite is related to the angular velocity ω by:
T=2πω
- If ω decreases, T increases. According to Kepler's third law:
T2∝R3
If T increases, the distance R must also increase.
- Match: (C) → (r) Will decrease.
- The gravitational potential energy E of a satellite is given by:
E=−GMmR
- As the distance R increases (from the previous step), the magnitude of the energy (which is negative) becomes less negative, indicating that the energy increases.
- Match: (D) → (s) Cannot say.
- (A) → (p)
- (B) → (q)
- (C) → (r)
- (D) → (s)
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (A) Chapter Exercises
68 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
In elliptical orbit of a planet, as the planet moves from apogee position to perigee position to perigee position, match the following columns
Column-IColumn-II(A)Speed of planet(p)Remains same(B)Distance of planet from centre of sun(q)Decreases(C)Potential energy(r)Increase(D)Angular momentum about centre of sun(s)Cannot say
View SolutionIf radius if earth is reduced to half without changing its mass, then match the following columns
Column-IColumn-II(A)Angular momentum of earth(p)Will become two times(B)Time period of rotation of earth(q)Will become four times(C)Rotational kinetic energy of earth(r)Will remain constant(D)(s)None
View SolutionA solid sphere is rotating about an axis shown in figure. An insect follows the dotted path on the circumference of sphere as shown in the figure.
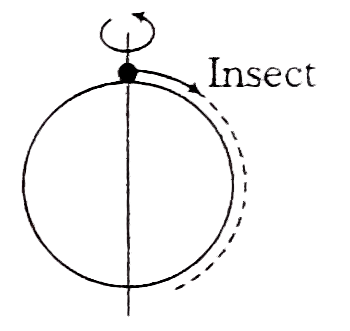
Column-IColumn-II(A)Moment of inertia(p)Will remain constant(B)Angular velocity(q)Will first increase, then decrease(C)Angular momentum(r)Will first decrease then increase(D)Rotational kinetic energy(s)Will continuously decrease(t)Will continuously increase
View SolutionTwo concentric spherical shells are as shown in figure. Match the following columns
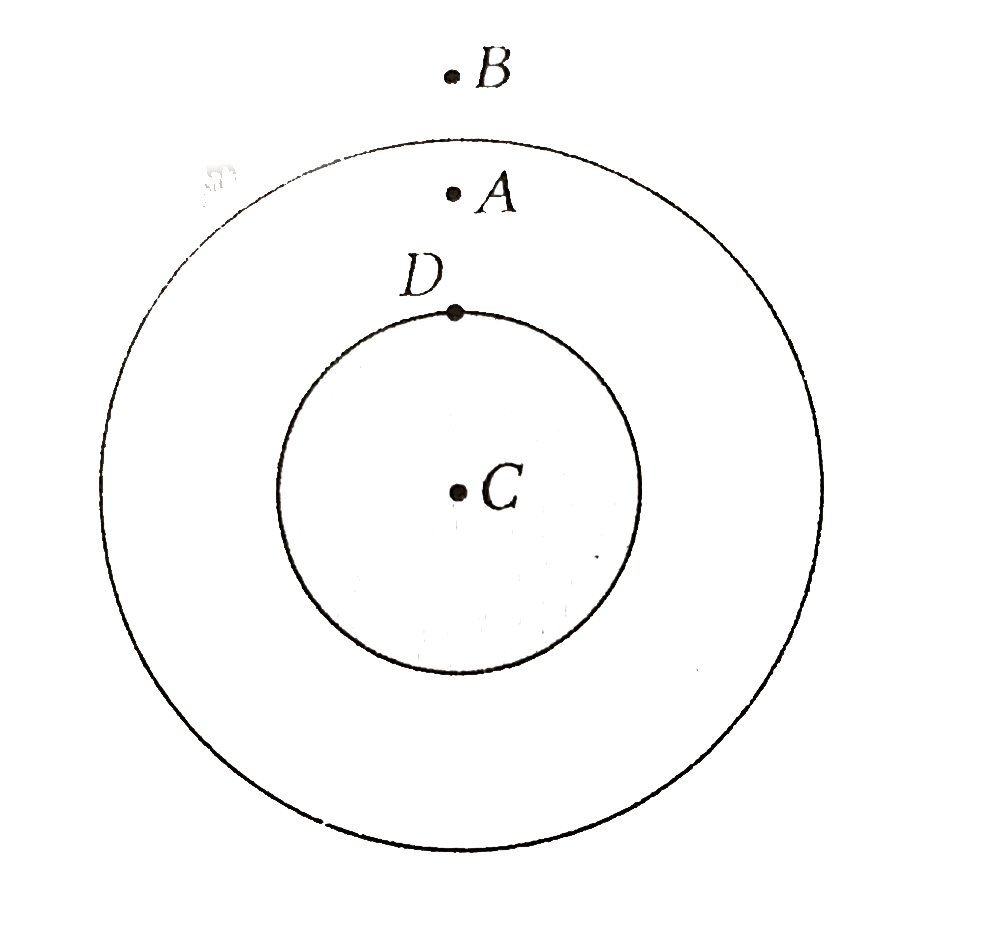
Column-IColumn-II(A)Potential at A(p)greater than B(B)Gravitational field at A(q)less than B(C)As one moves from C to D(r)Potential remains constant(D)As one moves from D to A(s)Gravitational field decreases(t)None
View SolutionMatch the Column-I with Column-II :
Column-IColumn-II(a)Mole fraction(p)mol kg−1(b)Molality(q)Depends on temperature(c)Molarity(r)Unitless(d)Normality(s)Independent of temperature
View SolutionMatch the following columns.
Column IColumn II(A)Longitudinal stress(p)Volume changes(B)Shear stress(q)Shape change(C)Volumetric stress(r)Volume does not changes(D)Tensile stress(s)Shapes does not change
View SolutionMatch the following :
Column -IColumn -II(A)Acceleration due to gravity(p)Kepler's law(B)Law of periods(q)Vector quantity(C)Orbital speed(r)Uniform near earth surface(D)Gravitational potential(s)Is nearly zero at infinity
View SolutionOn the surface of earth acceleration due gravity is g and gravitational potential is V. Match of following columns
Column-IColumn-II(A)At height h=R, value of g(p)Decreases by a factor14(B)At depth h=R2,value of g(q)Decrease by a factor12(C)At height h=R,value of V(r)Increase by a factor118(D)At height h=R2,value of V(s)Increase by a factor 2(t)None
View SolutionMatch the following :
{:(,"Column-I",,"Column-II"),((A),"Velocity",(p),"Increased,"n uarr z darr),((B), "Potential Energy",(q),"Increased,"ndarrzuarr),((C ),E_(n)-E_(n-1) (E="Total energy for H atom "(n cancel(=)1)),(r ),"Decreased,"n uarr ),((D),"Separation energy (For H atom)",(s),"No change"n uarr):}
View SolutionMatch the following columns
Column-IColumn-II(A)Time period of an earthsatellite in circular orbit(p)Independent of mass of satellite(B)Orbital velocity of satellite(q)Independent of radius of orbit(C)Mechanical energy of satellite(r)Independent of mass of earth(s)None
View Solution
