Question

If $I_0$ is the moment of inertia body about an axis passing through its center of mass. The moment about a parallel axis and at distance $d$ is $I=I_0+M{d}^2$. The variation of $I$ with $d$ is

Options

A.
B.
C.
D.

Explanation

To solve the problem, we need to analyze the relationship between the moment of inertia $$I$$ and the distance $$d$$ based on the given equation from the parallel axis theorem:

$$I=I_0+M{d}^2$$

1. Understanding the Equation:
- The equation \( I = I_0 + Md^2 \) indicates that the moment of inertia \( I \) about a parallel axis is equal to the moment of inertia \( I_0 \) about the center of mass plus a term that depends on the mass \( M \) and the square of the distance \( d \).

2. Identifying Variables:
- Here, \( I_0 \) is a constant (the moment of inertia about the center of mass).
- \( M \) is the mass of the body, which is also a constant.
- The term \( d^2 \) indicates that the moment of inertia varies with the square of the distance \( d \).

3. Analyzing the Variation:
- Since \( d^2 \) is a quadratic function, the equation can be rewritten as:
\( I = I_0 + M(d^2) \)
- This indicates that \( I \) is a function of \( d^2 \), which is a parabolic relationship.

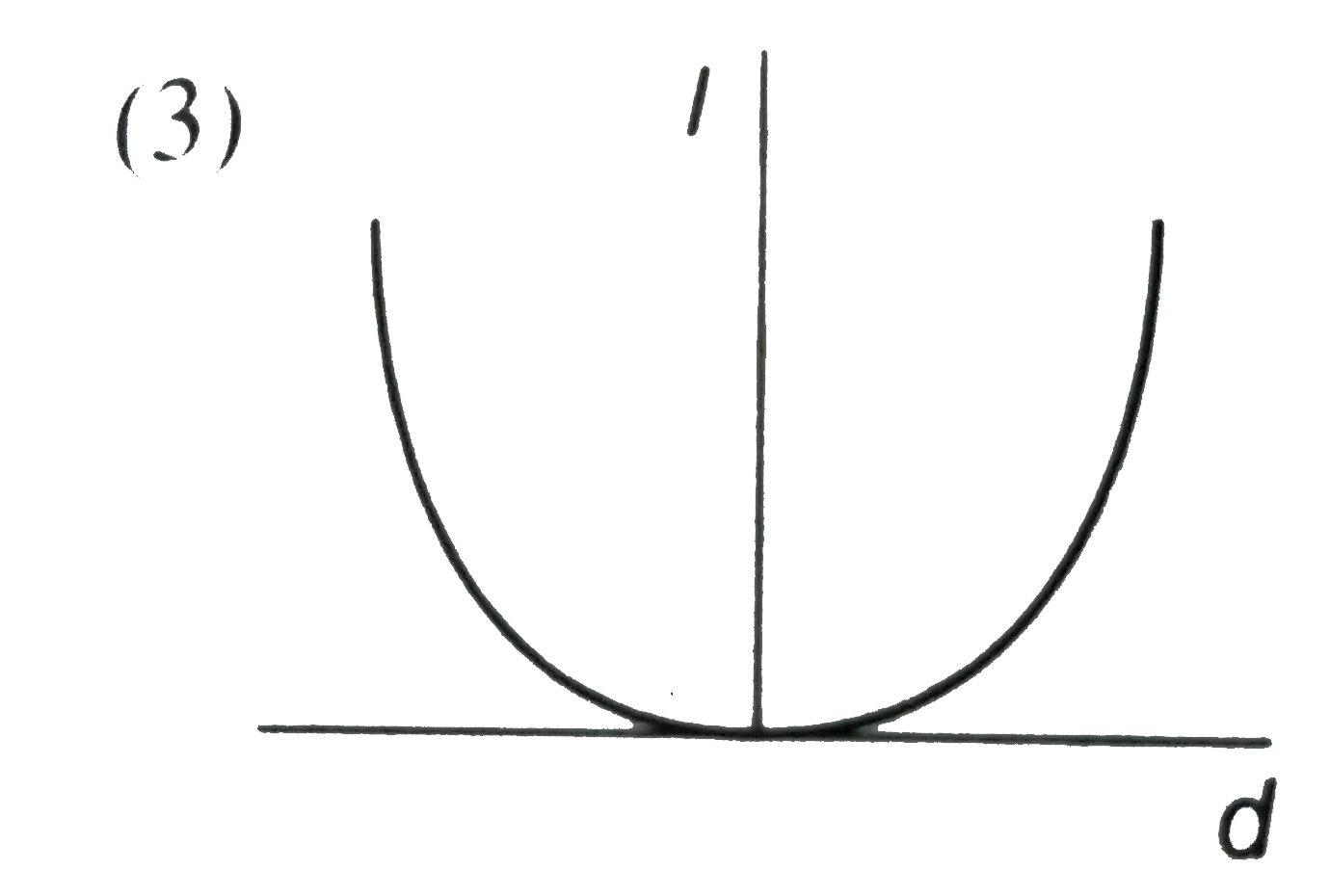
4. Graphical Representation:
- If we plot \( I \) on the y-axis and \( d \) on the x-axis, the graph will be a parabola opening upwards.
- At \( d = 0 \), \( I = I_0 \), meaning the graph will start at the point \( (0, I_0) \) and will not pass through the origin.

5. Conclusion:
- The variation of \( I \) with \( d \) is parabolic, and the graph does not pass through the origin. Therefore, the correct option for the variation of \( I \) with \( d \) is the one that represents a parabola starting from \( I_0 \).

Final Answer:
The variation of \( I \) with \( d \) is parabolic, starting from \( I_0 \) when \( d = 0 \).

---