If the coefficient of friction between M and the inclined surfaces is μ=1/√3 find the minimum mass m of the rod so that the of mass M=10kg remain stationary on the inclined plane

Angle of repose ϕ=tan−1(1√3)=30∘
Here θ>ϕ Hence , the block has a tendency to slide down

Mgcosθ+N',N=mgcosθ
N'=Mgcosθ+mgcosθ….(i)
For the block to remain stationary .
f=Mgsinθ...(ii)
If f is static as nature f<fmax
Mgsinθ<μN'
Mgsinθ<μ(Mgcosθ+mgcosθ)
Mgsinθ−μmgcosθ<μmgcosθn
m>M(tanθμ−1)⇒m>10(√31/√3−1)⇒m>20kg

Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.216videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.327videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Solved Examples12videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer5videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
Similar Questions
A block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View Solution
Knowledge Check
- Question 1 - Select One
In Fig . 7.151 , coefficient of kinetic friction between the 4 kg block and the inclined surface is 1√3 . Here 'm' is such a mass that the 4 kg block is moving up the plane with a constant speed , then m is :
 A2 kgB2.8 kgC3.4 kgD4 kg
A2 kgB2.8 kgC3.4 kgD4 kg - Question 2 - Select One
A block of mass m=2kg is resting on a rough inclined plane of inclination of 30∘ as shown in figure. The coefficient of friction between the block and the plane is μ=0.5. What minimum force F should be applied perpendicular to the plane on the block, so that blocks does not slip on the plane? (g=10m/s2)
 A2.68 NBZeroC4.34 ND6.24 N
A2.68 NBZeroC4.34 ND6.24 N
The coefficient of friction between m2 and inclined plane is μ (shown in the figure). If m1m2=sinθ then
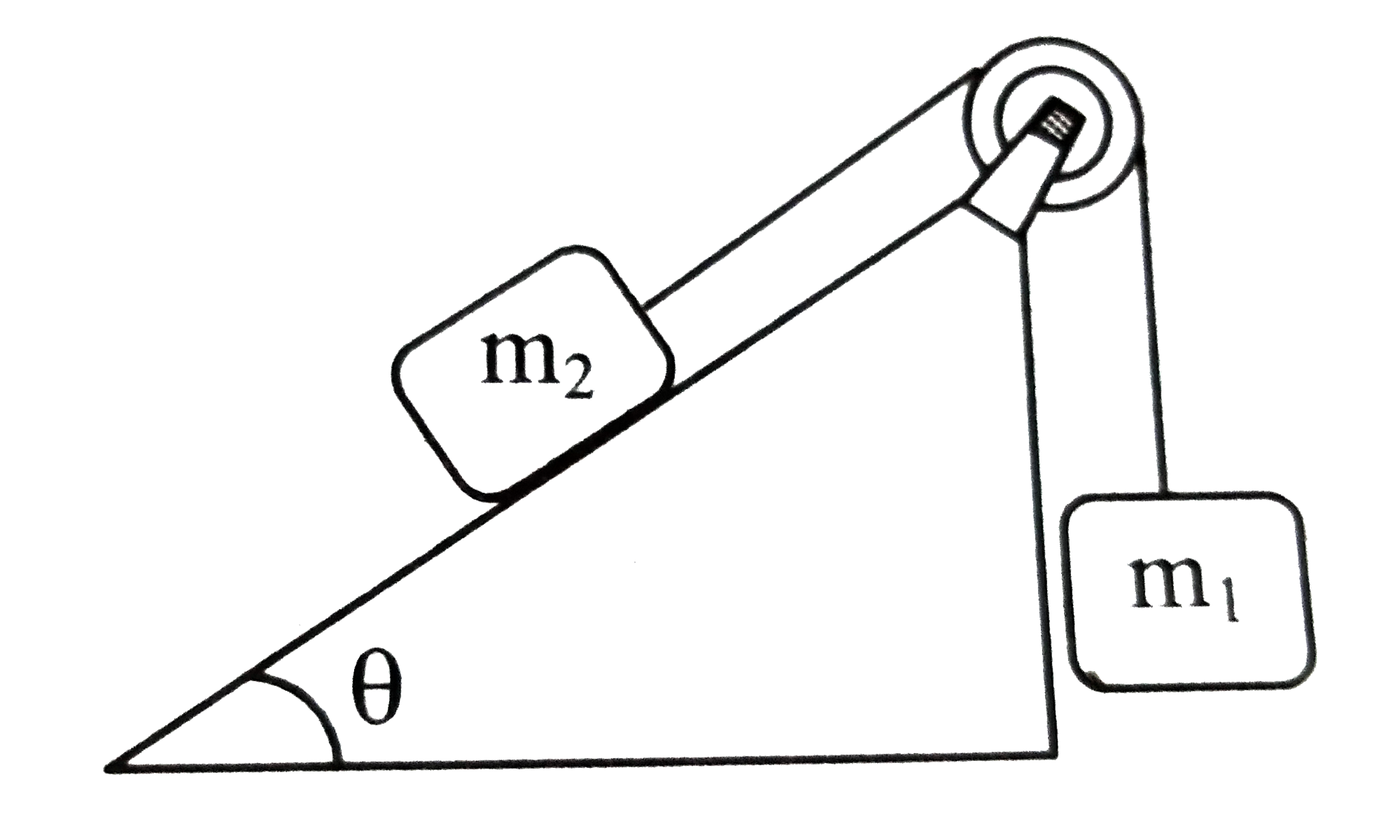 View Solution
View SolutionA block of mass m=2kg is resting on a inclined plane of inclination 30∘ as shown in figure The coefficient of friction between the block and the plane is μ=0.5 what minimum force F (in newton) should be applied perpendicular to the plane on the block so that the does not slip on the plane?
 View Solution
View SolutionA block of mass m=2kg is resting on a inclined plane of inclination 30∘ The coefficient of friction between the block and the plane is μ=0.5 what minimum force F (in newton) should be applied perpendicular to the plane on the block so that the does not slip on the plane?
 View Solution
View SolutionA block of mass m=2kg is resting on a inclined plane of inclination 30∘ as shown in figure The coefficient of friction between the block and the plane is μ=0.5 what minimum force F (in newton) should be applied perpendicular to the plane on the block so that the does not slip on the plane?
 View Solution
View SolutionTwo blocks of mass 'm' and 'M, are connect to the ends of a string passing over a pulley. 'M' lies on the plane inclined at an angle θ with the horizontal and 'm' is hanging vertically as shown in Fig. The coefficient of static friction between 'M' and the incline is μs. Find the minimum and maximum value of 'm' so that the system is at rest.
 View Solution
View SolutionA rectangular box lies on a rough inclined surface. The coefficient of friction between the surface and the box is (μ) Let the mass of the box be m.
At what angle of inclination θ of the plane to the horizontal will the box just start to slide down the plane ?View Solution

