In a children's park a heavy rod is pivoted at the centre and is made to rotate about the pivot so that the rod always remains horizontal. Two kids hold the rod near the ends and thus rotate with the rod figure. Let the mas of each kid be 15 kg, the distance between the points of the rod where the two kids hold it be 3.0 m and suppose that the rod rotates at the rate of 20 revolutions per minute. Find the force of friction exerted by the rod on one of the kids.

The correct Answer is:A, B
d=3m
→r=1.5m
r=Distanceformthecentre→o≠ofthek<br>n=20 rev per min<br>=20/60=1/3 rev/sec<br>omega=2pin=(2pi)/3rad/sec <br>:. FirctioN/Al force F=mromega^2<br>=15xx(15)xx((2pi)^2)/9<br>=5xx(0.5)x4pi^2=10pi^2<br>:. Friction force on one of the kids is 10π2.
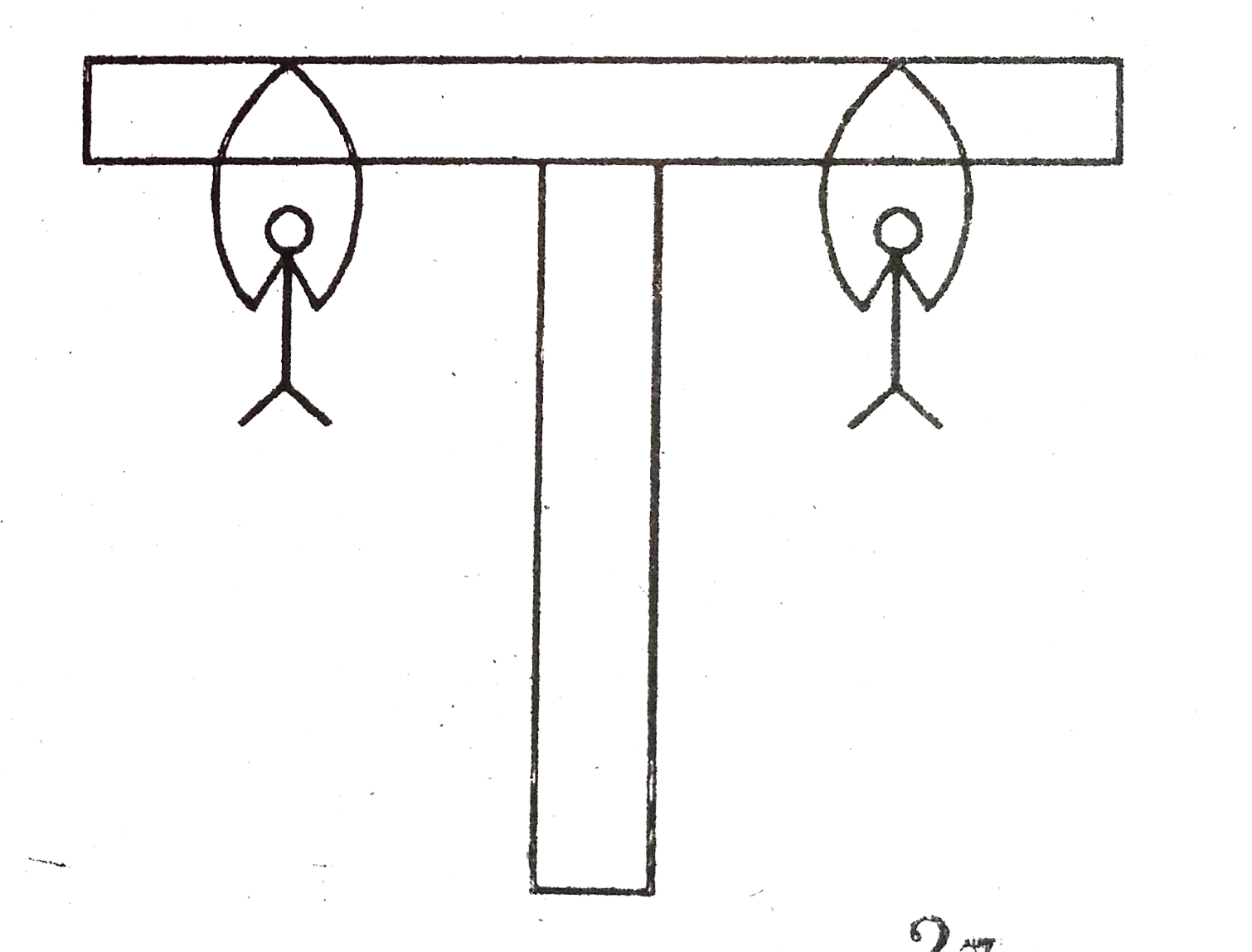
Topper's Solved these Questions
- CIRCULAR MOTIONBook:HC VERMA ENGLISHChapter:CIRCULAR MOTIONExercise:Question for short Answer
Explore 10 Videos
- CIRCULAR MOTIONBook:HC VERMA ENGLISHChapter:CIRCULAR MOTIONExercise:Objective -2
Explore 6 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBook:HC VERMA ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONExercise:Objective -2
Explore 11 Videos
- FLUID MECHANICSBook:HC VERMA ENGLISHChapter:FLUID MECHANICSExercise:All Questions
Explore 90 Videos
Similar Questions
A particle is attached to an end of a rigid rod. The other end of the rod is hunged and the rod rotates always remaining horizontal. Its angular speed is increasing at contant rate. The mass of the particle is m . The force exerted by the rod on the particle is →F , then:
View SolutionA uniform rod AB of length l and mass m is free to rotate about point A. The rod is released from rest in the horizontal position. Given that the moment of inertia of the rod about A is ml23, the initial angular acceleration of the rod will be

View SolutionA rod of length L is pivoted at one end and is rotated with as uniform angular velocity in a horizontal plane. Let T1andT2 be the tensions at the points L/4 and 3L/4 away from the pivoted ends.
View SolutionA rod is pivoted about its centre. A 10 N force is applied 4 m from the pivot and another force of 5 N is applied 2 m from the pivot, as shown. The magnitude of the total torque about the pivot is

View SolutionFigure shows a rigid rod of length 1.0 m. It is pivoted at O. For what value m, the rod will be in equilibrium ? Find the force (F) exerted on the rod by the pivot. Neglect the weight of the rod.
View SolutionA rod of mass m and length L is pivoted at the bottommost point O and can freely rotate about the point O. The rod is disturbed from the vertical position so that it starts rotating about O. When it makes an angle θ with the vertical
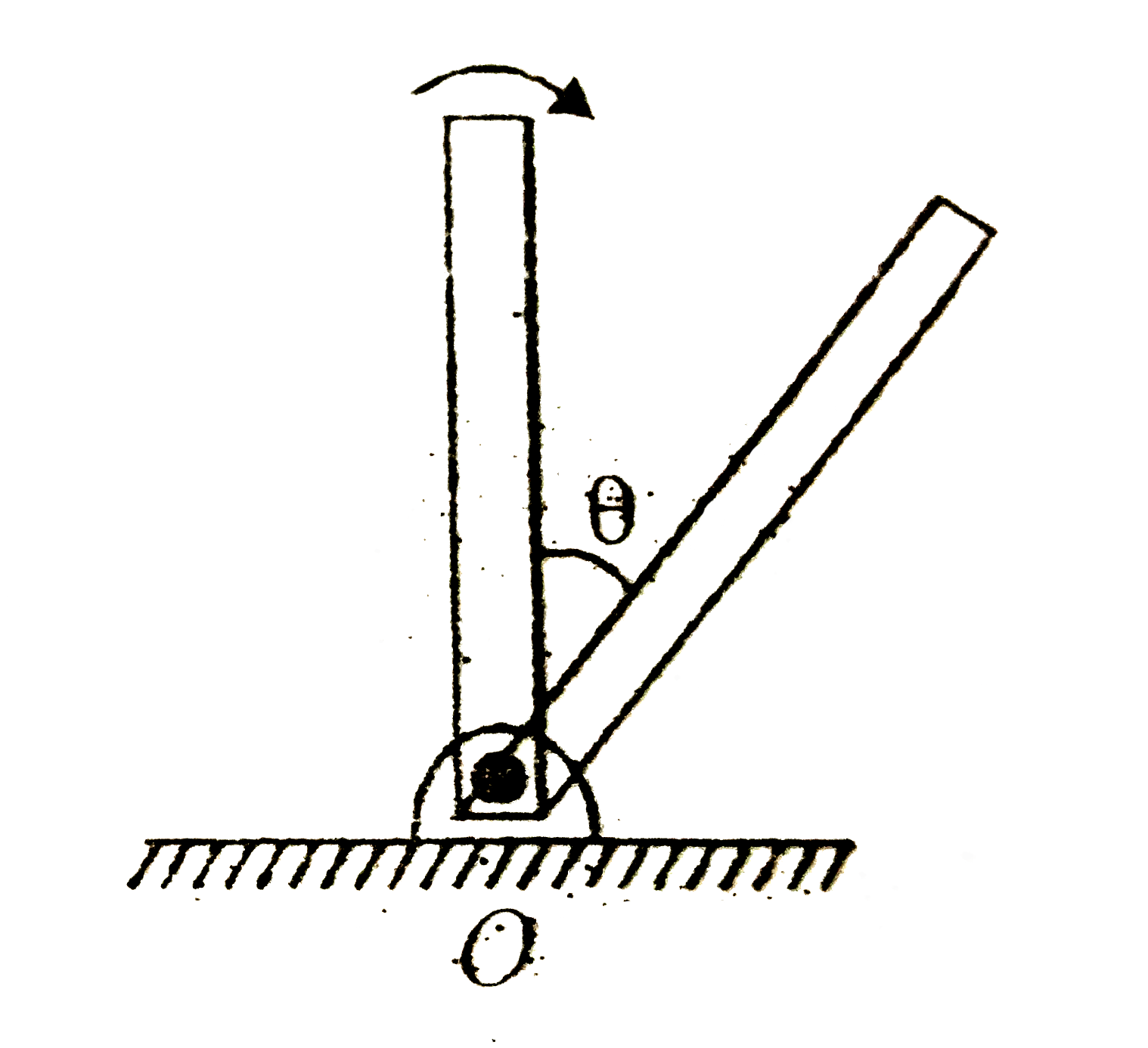
View SolutionTwo rods are rotating about two fixed points in opposite directions. If they start from their position of coincidence and one rotates at the rate double that of the other, then find the locus of point of the intersection of the two rods.
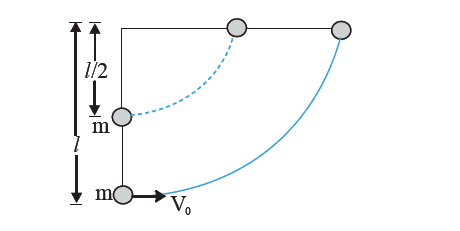
View SolutionA light rod of length l is pivoted at the upper end. Two masses (each m), are attached to the rod, one at the middle and the other at the free end. What horizontal velocity must be imparted to the lower end mass, so that the rod may just take up the horizontal position ?
View SolutionA thin rod MN free to rotation in the vertical plane about the fixed end N is held horizontal when the end M is released the speed of this end when the rod makes an angle α with the horizontal will be proportional to : (see figure)

View SolutionA uniform rod mass m and length l is provided at one end and is rotated with constant angular velocity ω in a horizontal plane. Tension in the rod at a distance (√3l/2) from pivoted end is (Assume gravity free space)
View Solution