In a double star, two stars one of mass m1 and another of mass m2, with a separation d, rotate about their common centre of mass. Find
(a) an expression for their time period of revolution.
(b) the ratio of their kinetic energies.
(c) the ratio of their angular momenta about the centre of mass.
(d) the total angular momentum of the system.
(e) the kinetic energy of the system.
The correct Answer is:A, B, C, D
r1+r2=d ..(i)
m1r1=m2r2 ..(ii)

Solving these two equations we get,
r1=(m2m1+m2)d or r2=(m1m1+m2)d
The centripetal force is provided by gravitational firce,
m1r1ω2=m2r2ω2=Gm1m2d2
Solving these equations, we get
ω=√G(m1+m2)d3
∴T=2πω=2π√d3G(m1+m2)
(b) K1K2=12I1ω212I2ω2=I1I2=m1r21m2r22
=(m1m2)(r1r2)2=(m1m2)(m2m1)2=m2m1
(c ) L1L2=L1ωI2ω=I1I2=m2m1
(d) L=L1+L2=(I1+L2)ω
=(m1r21+m2r22)ω
=[m1m22d2(m1+m2)2+m2m21d2(m1+m2)2]ω
=μωd2
where, μ=m1m2m1+m2= reduced mass
(e) K=12(I1+I2)ω2=12μω2d2
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.1
20 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.2
20 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 2 More Than One Correct
10 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
In a double star system one of mass m1 and another of mass m2 with a separation d rotate about their common centre of mass. Then rate of sweeps of area of star of mass m1 to star of mass m2 about their common centre of mass is
View Solution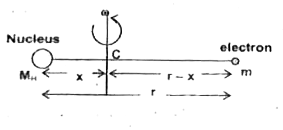
The angular momentum of the atom about the centre of mass will be
View Solution
Knowledge Check
Two stars of masses m1 and m2 distance r apart, revolve about their centre of mass. The period of revolution is :
A2π√r32G(m1+m2)B2π√r3(m1+m2)2G(m1m2)C2π√2r3G(m1+m2)D2π√r3G(m1+m2)Two bodies have their moments of inertia I and 2I respectively about their axis of rotation. If their kinetic energies of rotation are equal, their angular momenta will be in the ratio.
A12B√2C1:√2D21
In a binary star system one star has thrice the mass of other. The stars rotate about their common centre of mass then :
View SolutionTwo bodies A and B having masses in the ratio of 3 : 1 possess the same kinetic energy. The ratio of their linear momenta is then
View SolutionTwo stars of masses m1 and m2 distance r apart, revolve about their centre of mass. The period of revolution is :
View SolutionTwo bodies of masses m1andm2 have same kinetic energy. The ratio of their momentum is
View Solution_E01_055_Q01.png)
For the double star system, the two stars having masses m1 and m2are separated b a distance r. They are revolving about their common centre of mass in radii r1 and r2 respectively. Which of the following is/are incorrect.?
View SolutionA binary star consists of two stars A(mass2.2Ms) and B (mass11Ms) where Ms is the mass of the sun, they are separted by distane d and are rotating about their center of mass, which is stationary. The ratio of the total angular momentum of the binary to the angular momentum of star B about the centre of mass is
View Solution