In a meter bridge, null point is 20cm, when the known resistance R is shunted by 10Ω resistance, null point is found to be shifted by 10 cm. Find the unknown resistance X.
To solve the problem step by step, we will use the principles of a meter bridge and the concept of shunting resistances.
Step 1: Understand the Initial Condition
In the initial condition, the null point is at 20 cm on the meter bridge. This means that the ratio of the known resistance R to the unknown resistance X can be expressed as:
RX=L1100−L1
where L1=20cm.
Step 2: Substitute the Values
Substituting L1 into the equation gives:
RX=2080=14
From this, we can express R in terms of X:
R=X4(Equation 1)
Step 3: Understand the Condition with Shunting
When the known resistance R is shunted by a resistance S=10Ω, the new equivalent resistance r is given by:
1r=1R+1S
This can be rearranged to:
r=RSR+S
Substituting S=10Ω:
r=R⋅10R+10
Step 4: Analyze the New Condition
After shunting, the null point shifts to L2=30cm (20 cm + 10 cm). The new ratio can be expressed as:
rX=L2100−L2
Substituting L2:
rX=3070=37
From this, we can express r in terms of X:
r=3X7(Equation 2)
Step 5: Equate the Two Expressions for r
Now we have two expressions for r:
1. r=10RR+10
2. r=3X7
Setting them equal gives:
10RR+10=3X7
Step 6: Substitute R from Equation 1
Substituting R=X4 into the equation:
10⋅X4X4+10=3X7
This simplifies to:
10X4X+404=3X7
Cross-multiplying gives:
10X⋅7=3X⋅(X+40)
This leads to:
70X=3X2+120X
Rearranging gives:
3X2+50X=0
Step 7: Factor the Equation
Factoring out X:
X(3X+50)=0
This gives two solutions:
1. X=0 (not valid)
2. 3X+50=0 leads to X=50Ω
Conclusion
The unknown resistance X is:
50Ω
In the initial condition, the null point is at 20 cm on the meter bridge. This means that the ratio of the known resistance R to the unknown resistance X can be expressed as:
RX=L1100−L1
where L1=20cm.
Substituting L1 into the equation gives:
RX=2080=14
From this, we can express R in terms of X:
R=X4(Equation 1)
When the known resistance R is shunted by a resistance S=10Ω, the new equivalent resistance r is given by:
1r=1R+1S
This can be rearranged to:
r=RSR+S
Substituting S=10Ω:
r=R⋅10R+10
After shunting, the null point shifts to L2=30cm (20 cm + 10 cm). The new ratio can be expressed as:
rX=L2100−L2
Substituting L2:
rX=3070=37
From this, we can express r in terms of X:
r=3X7(Equation 2)
Now we have two expressions for r:
1. r=10RR+10
2. r=3X7
10RR+10=3X7
Substituting R=X4 into the equation:
10⋅X4X4+10=3X7
This simplifies to:
10X4X+404=3X7
Cross-multiplying gives:
10X⋅7=3X⋅(X+40)
This leads to:
70X=3X2+120X
Rearranging gives:
3X2+50X=0
Factoring out X:
X(3X+50)=0
This gives two solutions:
1. X=0 (not valid)
2. 3X+50=0 leads to X=50Ω
The unknown resistance X is:
50Ω
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Example Type 1
2 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Example Type 2
1 Video
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
In a meter bride, null point is 20cm, when the known resistance R is shunted by 10Ω resistance, null point is found to be shifted by 10cm . Find the unknown resistance X.
View SolutionIn a meter bridge, null point is at l=33.7cm, when the resistance S is shunted by 12Ω resitance the null point is found to be shifted by a distance of 18.2cm. The value of unknown resistance R should be
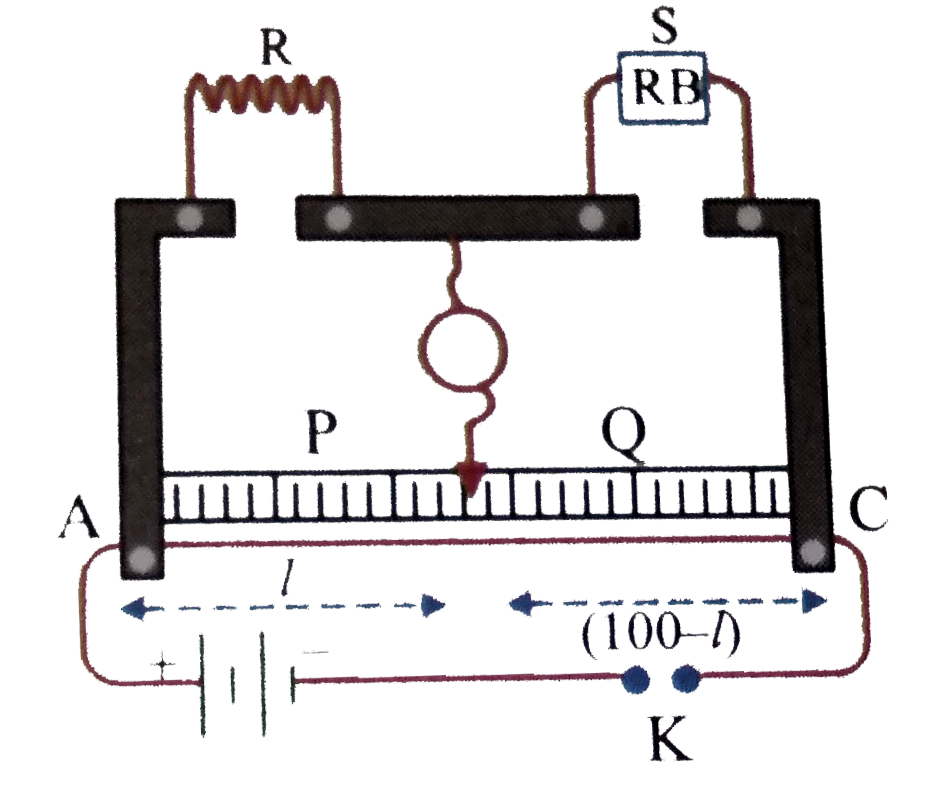
View SolutionFigure 6.32 shows a meter bridge in the (which is nothing but a particle wheastone bridge), consisting of two resistors X and Y together in parellel with a meter long constantan wire of uniform cross section.
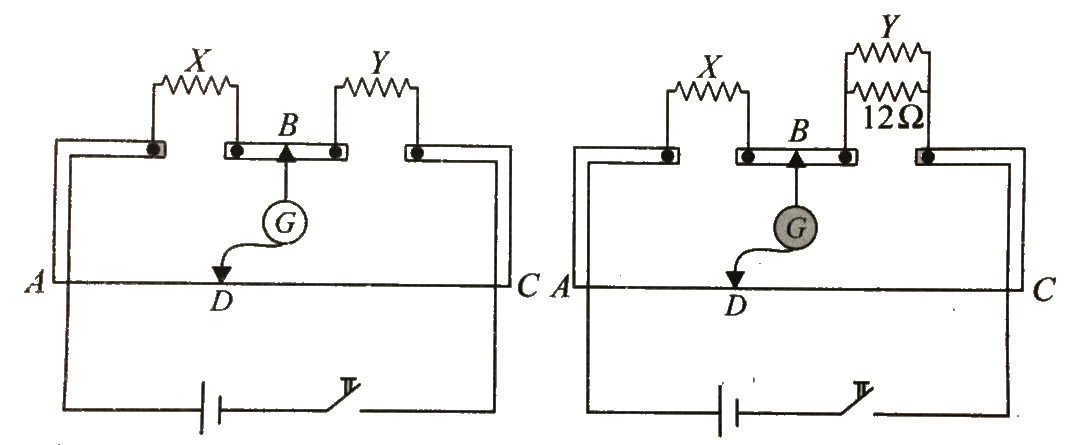
with the help of a movable contact d, one can change the ratio of resistance of the two segments of the wire until a sensitive galvanometer G connected across b and D shows no deflection. The null point is found to be at a distance of 33.7cm. The resistor Y is shunted by a resistance of 12Ω, and the null point is found to shift by a distance of 18.2cm. Determine the resistance of X and Y.
View SolutionIn the metre bridge, the balancing length AB = 20 cm. The unknown resistance X is equal to
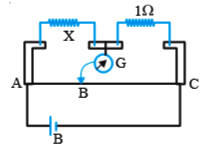
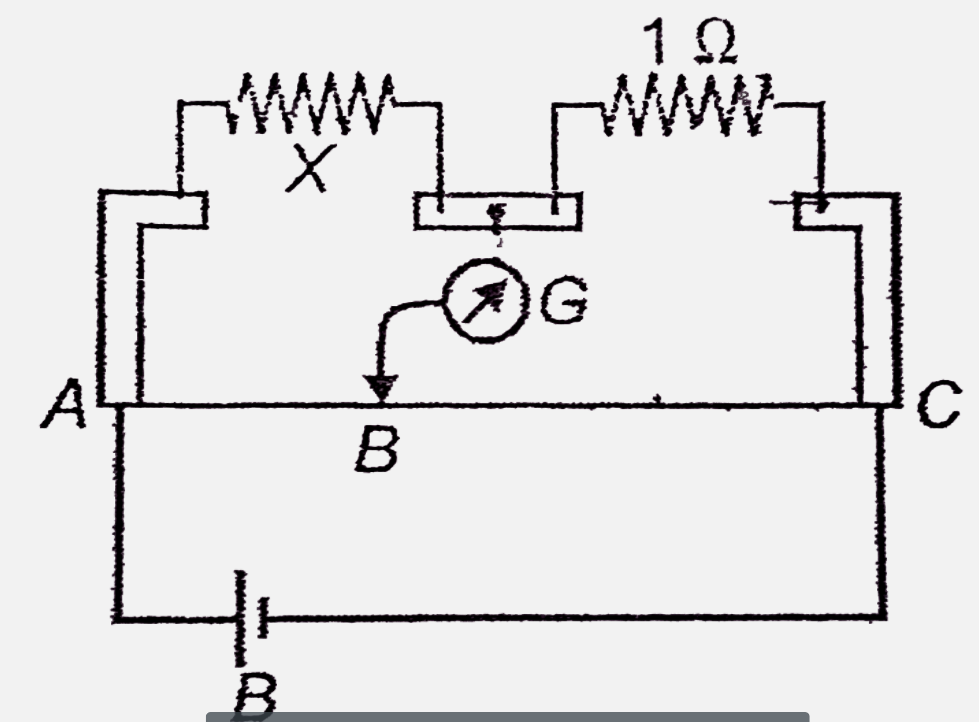
View SolutionIn the metre bridge, the balancing length AB =l=20 cm. The unknown resistance X is equal to
View SolutionThe figure shows experimental set up of a meter bridge. When the two unknown resistances X and Y are inserted, the null point D is obtained 40 cm from the end A. When a resistance of 10Ω is connected in series with X, the null point shifts by 10 cm. Find the position of the null point when the 10Ω resistance is instead connected in series with resistance 'Y'. Determine the value of the resistance X and Y
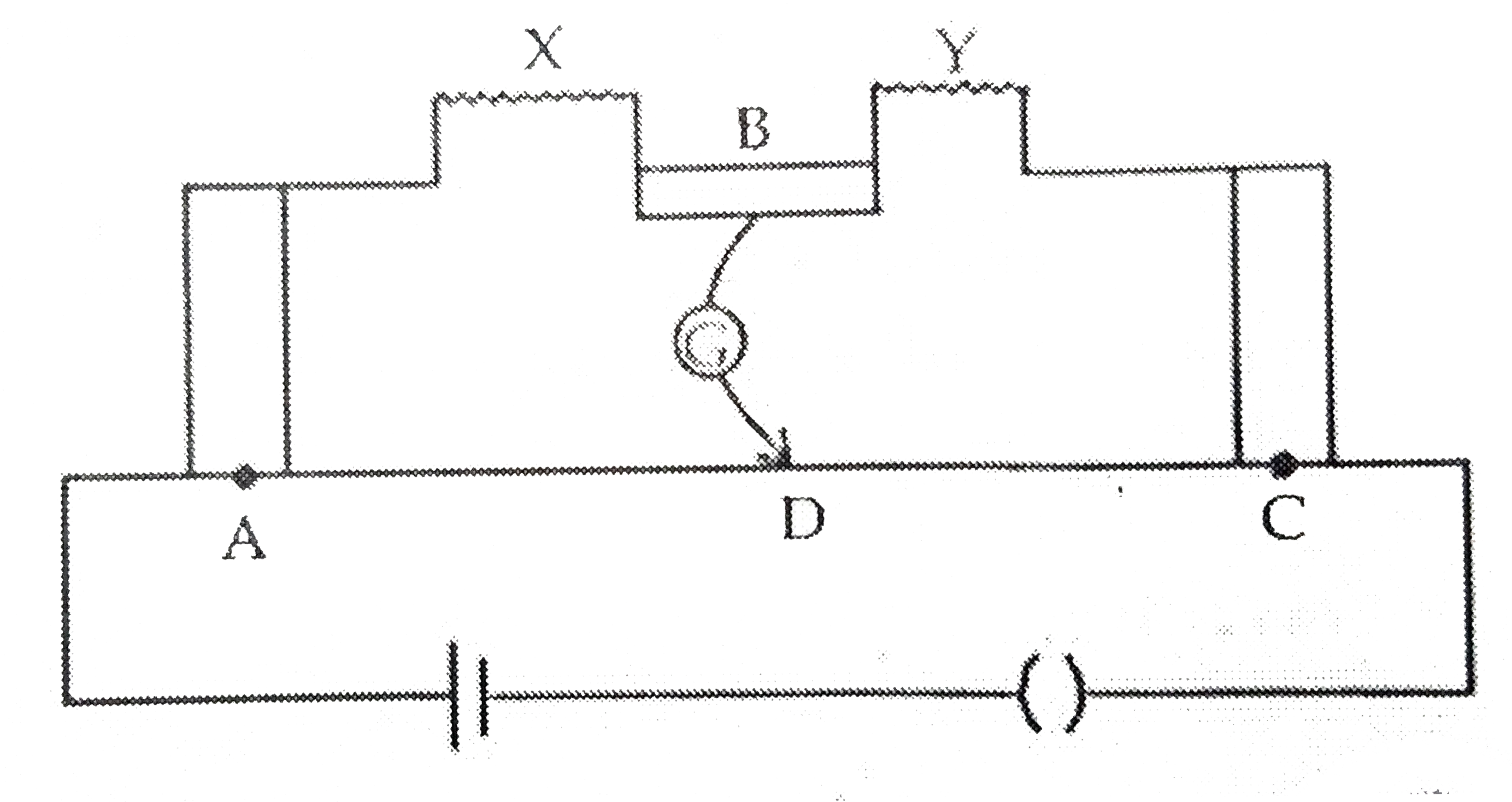
View SolutionIn an experiment to measure the internal resistance of a cell by a potentiometer, it is found that the balance point is at a length of 2m when the cell is shunted by a 5Ω resistance and is at a length of 3m when the cell is shunted by a 10Ω resistance, the internal resistance of the cell is then
View SolutionIn an experiment to measure the internal resistance of a cell by potentiometer, it is found that the balance point is at a length of 2 m when the cell is shunted by a 4Ω resistance and at 3 m when cell is shunted by a 8Ω resistance. The internal resistance of cell is -
View SolutionThe figure
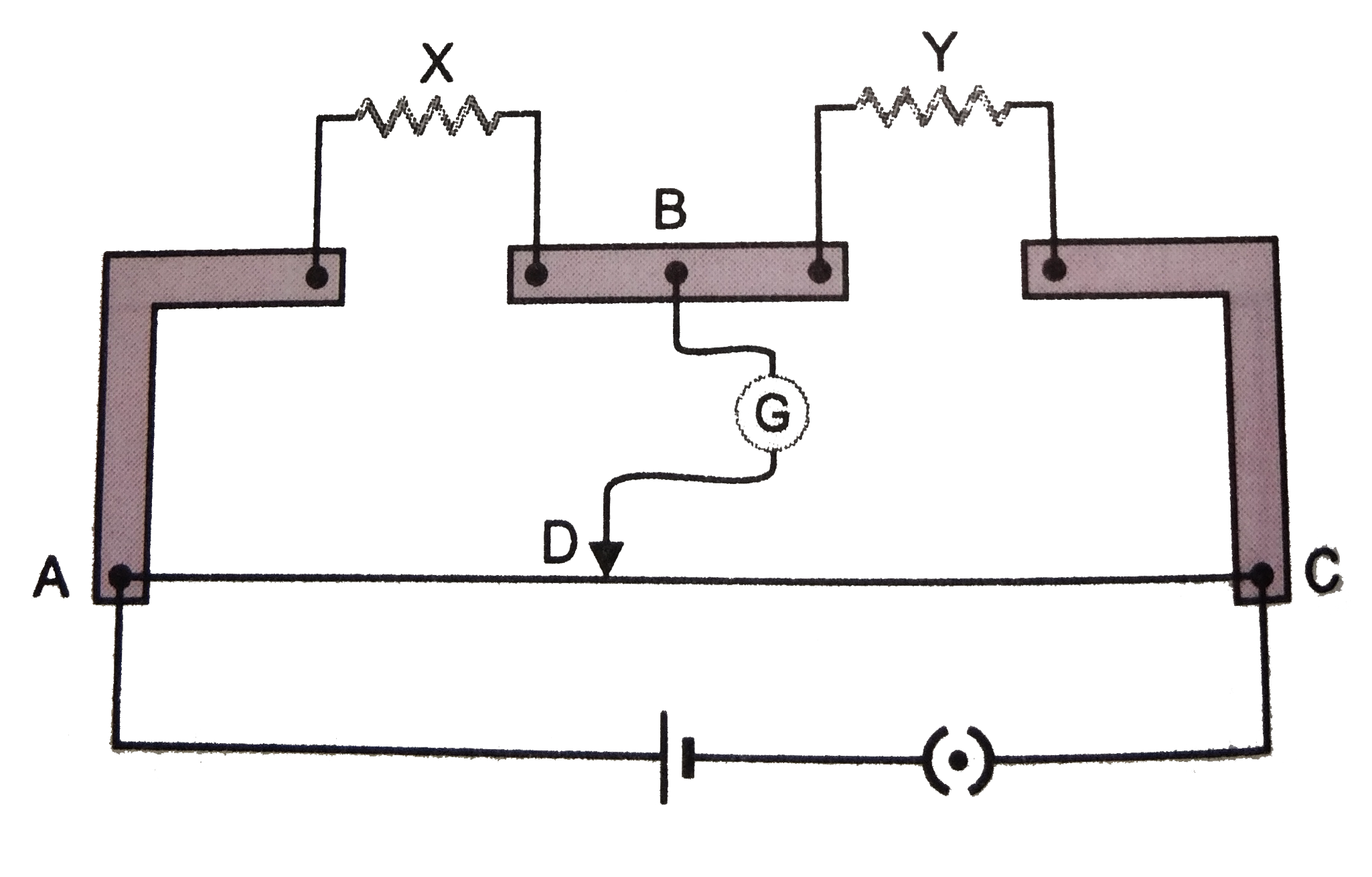
Shows the experimental set up of a meter bridge. The null point is found to be 60 cm away from the end A with X and Y in positions as shown. When a resistance of 15Ω is connected in series with Y, the null points is found to shift by 10 cm towards the end A of the wire. Find the position of the null point if resistance of 30Ω were connected in parallel with Y.
View SolutionIn a meter bridge experiment, null point is obtained at 20cm from one end of the wire when resistance X is balanced against another resistance Y. If X<Y, then the new position of the null point from the same end, if one decides to balance a resistance of 4X against Y will be at.
View Solution
