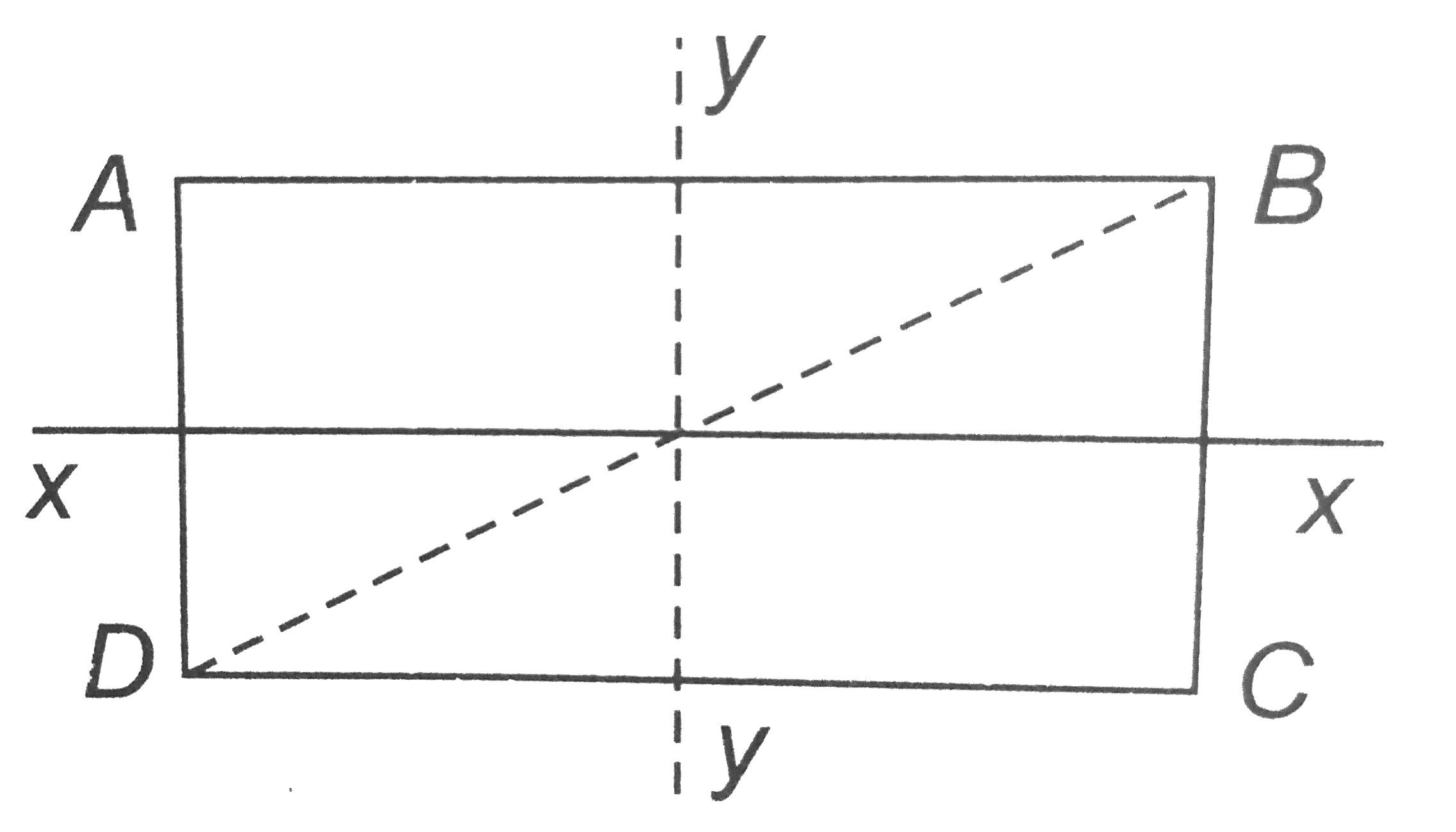
In a rectangle ABCD,AB=2l and BC=l. Axes × and yy pass through centre of the rectangle. The moment of inertia is least about :
 .
.
DB
BC
xx
yy
The correct Answer is:C
The distributing of mass is nearest xx.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct9videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Linked Comprehension28videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective13videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
Similar Questions
Let l be the moment of inertia of a uniform square plate about an axis AB that passes through its centre and is parallel to two of its sides. CD is a line in the plane of the plate that passes through the centre of the plate and makes an angle θ with AB. The moment of inertia of the plate about the axis CD is then equal to
View SolutionLet l be the moment of inertia of a uniform square plate about an axis AB that passes through its centre and is parallel to two of its sides. CD is a line in the plane of the plate that passes through the centre of the plate and makes an angle θ with AB. The moment of inertia of the plate about the axis CD is then equal to
View Solution
Knowledge Check
- Question 1 - Select One
Ler l be the moment of inertia of a uniform square plate about an axis AB that passes through its centre and is parallel to two of its sides. CD is a line in the plane of the plate that passes through the centre of the plate and makes an angle θ with AB. The moment of inertia of the plate about the axis CD is then equal to
AIBIsin2θCIcos2θDIcos2(θ2).
Consider a uniform rod of mass m and length 2l with two particles of mass m each at its ends. Let AB be a line perpendicular to the length of rod and passing through its centre. Find the moment of inertia of the system about AB.
View SolutionABCD is a rectangle with A(−1,2),B(3,7) and AB:BC=4:3. If P is the centre of the rectangle, then the distance of P from each corner is equal to
View SolutionIf I1 is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mass and I2 is the moment of inertia of the ring about an axis perpendicular to plane of ring and passing through its centre formed by bending the rod, then
View Solutionif l1 is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mass and l2 te moment of inertia of the ring formed by the same rod about an axis passing through the centre of mass of the ring and perpendicular tot he plane of the ring. then find the ratio l1l2.
View SolutionA wire of length l and mass m is bent in the form of a rectangle ABCD with ABBC=2. The moment of inertia of this wife frame about the side BC is
View SolutionIn rectangle ABCD, slope of AB=56. State the slope of
BC .View SolutionChoose the correct option:
A wire of mass m and length l is bent in the form of a quarter circle. The moment of the inertia of the wire about an axis is passing through the centre of the quarter circle is approximatelyView Solution

