In a Wheatstone's bridge, three resistances P,Q and R connected in the three arms and the fourth arm is formed by two resistances S1andS2 connected in parallel. The condition for the bridge to be balanced will be
R(s1+s2)s1s2
s1s2R(s1+s2)
Rs1s2(s1+s2)
(s1+s2)Rs1s2
The correct Answer is:A
To find the condition for a Wheatstone bridge to be balanced when three resistances P,Q,R are connected in three arms and the fourth arm is formed by two resistances S1 and S2 connected in parallel, we can follow these steps:
1. Understanding the Wheatstone Bridge Configuration:
- Draw the Wheatstone bridge circuit with resistances P,Q,R in three arms and S1 and S2 in parallel in the fourth arm.
2. Condition for Balance:
- The bridge is balanced when the current through the galvanometer IG is zero. This means that the potential difference across the galvanometer is zero.
3. Using the Balance Condition:
- For the bridge to be balanced, the ratio of the resistances in one arm must equal the ratio of the resistances in the other arm:
PQ=RSeq
where Seq is the equivalent resistance of S1 and S2 in parallel.
4. Calculating the Equivalent Resistance:
- The equivalent resistance Seq of two resistances S1 and S2 in parallel is given by:
Seq=S1⋅S2S1+S2
5. Substituting Seq into the Balance Condition:
- Substitute Seq into the balance condition:
PQ=RS1⋅S2S1+S2
6. Cross-Multiplying:
- Cross-multiply to eliminate the fraction:
P⋅(S1⋅S2S1+S2)=Q⋅R
7. Rearranging the Equation:
- Rearranging gives:
P⋅(S1+S2)=Q⋅R⋅S1⋅S2S1⋅S2
8. Final Formulation:
- This leads to the final balanced condition:
P⋅(S1+S2)=Q⋅R⟹PQ=R⋅(S1+S2)S1⋅S2
Final Answer:
The condition for the Wheatstone bridge to be balanced is:
PQ=R⋅(S1+S2)S1⋅S2
- Draw the Wheatstone bridge circuit with resistances P,Q,R in three arms and S1 and S2 in parallel in the fourth arm.
- The bridge is balanced when the current through the galvanometer IG is zero. This means that the potential difference across the galvanometer is zero.
- For the bridge to be balanced, the ratio of the resistances in one arm must equal the ratio of the resistances in the other arm:
PQ=RSeq
where Seq is the equivalent resistance of S1 and S2 in parallel.
- The equivalent resistance Seq of two resistances S1 and S2 in parallel is given by:
Seq=S1⋅S2S1+S2
- Substitute Seq into the balance condition:
PQ=RS1⋅S2S1+S2
- Cross-multiply to eliminate the fraction:
P⋅(S1⋅S2S1+S2)=Q⋅R
- Rearranging gives:
P⋅(S1+S2)=Q⋅R⋅S1⋅S2S1⋅S2
- This leads to the final balanced condition:
P⋅(S1+S2)=Q⋅R⟹PQ=R⋅(S1+S2)S1⋅S2
The condition for the Wheatstone bridge to be balanced is:
PQ=R⋅(S1+S2)S1⋅S2
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Match the columns
4 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
In a Wheatstone bridge, three resistance, P, Q and R are connected in the three arms and fourth arm is formed by two resistance s1ands2 connected in parallel. The condition for the bridge to be balanced for ratio (pQ) is (given R=10Ω,S1=6Ω,S2=3Ω)
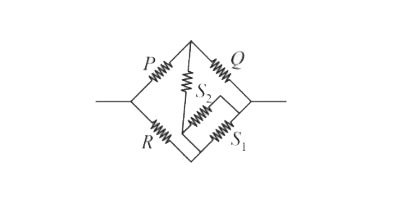
View SolutionIn a Wheatstone bridge, three resistance, P, Q and R are connected in the three arms and fourth arm is formed by two resistance s1ands2 connected in parallel. The condition for the bridge to be balanced for ratio (pQ) is (given R=10Ω,S1=6Ω,S2=3Ω)

View SolutionResistance R,2R,4R,8R ...... ∞ are connected in parallel. What is their resutlant resistance will be
View SolutionThe wire of same dimension but resistivities(p1) and (p2)are connected in parallel. The equivalent resistivity of the combination is
View SolutionThree resistance P,Q,R each of 2Ω and an unknown resistance S from the four amrs of a Wheatstone's bridge circuit. When a resistance of 6Ω is connected in parallel to S the bridge gets balanced. What is the value of S ?
View SolutionThree resistance P,Q,R each of 2Ω and an unknown resistance S from the four amrs of a Wheatstone's bridge circuit. When a resistance of 6Ω is connected in parallel to S the bridge gets balanced. What is the value of S ?
View SolutionIn a balanced wheatstone's network, the resistances in the arms Q and S are interchanged. As result of this:
View SolutionA 6Ω resistance is connected in the left gap of a meter bridge. In the second gap 3Ω and 6Ω are joined in parallel. The balance point of the bridge is at _______
View SolutionConsider a Wheatstone bridge with resistance and capacitance connected as shown Find the condition on the resistance and the capacitance such that the bridge remains balanced at all times.
View SolutionThe Total resistance when connected in series in 9Ω and when connected in parallel is 2Ω The value of two resistance are
View Solution