In a YDSE experiment, d = 1mm, λ= 6000Å and D= 1m. The minimum distance between two points on screen having 75% intensity of the maximum intensity will be
0.50 mm
0.40 mm
0.30 mm
0.20 mm
The correct Answer is:D
34Imax=Imaxcos2(ϕ2)
∴ϕ2=π12 and 5π6
∴ϕ=π6
and 5π3=(2πλ)(Δx)=(2πλ)ydD
∴y1=λD12d=(6000×10−10)(1)(12)(10−3)
=0.05×(10−3)m=0.05mm
y2=5(λD12d)=5×0.05mm
=0.25mm
Δy=y2−y1=0.2mm .
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - LEVEL 2 (single correct option)1videos
INTERFERENCE AND DIFFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 More Than One Correct6videos
INTERFERENCE AND DIFFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Subjective Questions5videos
INTERFERENCE AND DIFFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery59videos
MAGNETIC FIELD AND FORCES
Similar Questions
In Young's double-slit experiment λ=500nm,d=1mm, and D=4m. The minimum distance from the central maximum for which the intensity is half of the maximum intensity is '∗'×10−4m. What is the value of '∗'?
View SolutionIn a Young's double slit experiment λ=500nm,d=1.0mmandD=1.0m. Find the minimum distance from the central maximum for which the intensity is half of the maximum intensity.
View SolutionIn a double experiment D=1m, d=0.2 cm and λ=6000Å. The distance of the point from the central maximum where intensity is 75% of that at the centre will be:
View SolutionIn YDSE a=2mm, D = 2m, λ=500 mm. Find distance of point on screen from central maxima where intensity becomes 50% of central maxima
View SolutionIn a Young's double slit experiment, slits are seperated by a distance d and screen is at distance D, (D>>d) from slit plane. If light source of wavelength λ(λ<<d) is used. The minimum distance from central point on the screen where intensity is one fourth of the maximum is Dλnd. Find the value of n.
View SolutionIn YDSE path difference at a point on screen is λ8 . Find ratio of intensity at this point with maximum intensity.
View SolutionIn YDSE, D=1m,d=1mm, and λ=5000nm. The distance of the 100th maxima from the central maxima is
View SolutionIn a YDSE, D=1M,d=1mm,andλ=1/2mm.
(a) Find the distance between the first and central maxima on the screen.
(b) Find the number of maxima and minima obtained on the screen.View SolutionYoung's double-slit experiment setup with ligth of wavelength λ=6000Å, distance between two slit in 2 mm and distance between the plane of slits and the screen. Is 2 m. The slits are of equal intensity. When a sheet of glass of refractive index 1.5 (which permtis only a fraction η of the incident light to pass through) and thickness 8000Å is placed in front of the lower slit, it is observed that the intensity at a point P, 0.15 mm above the central maxima, does not change.
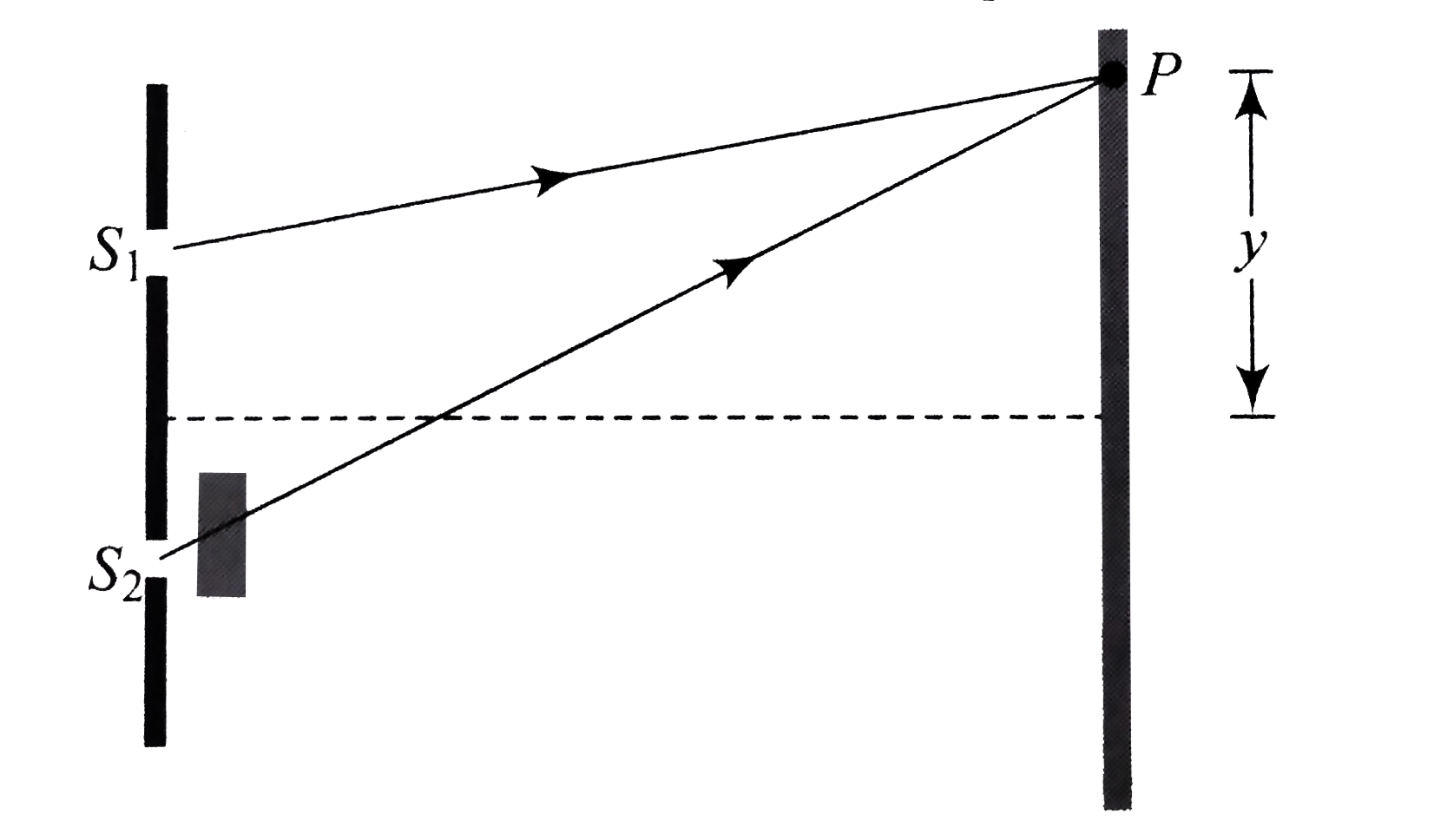
Intensity at point P isView SolutionYoung's double-slit experiment setup with ligth of wavelength λ=6000Å, distance between two slit in 2 mm and distance between the plane of slits and the screen. Is 2 m. The slits are of equal intensity. When a sheet of glass of refractive index 1.5 (which permtis only a fraction η of the incident light to pass through) and thickness 8000Å is placed in front of the lower slit, it is observed that the intensity at a point P, 0.15 mm above the central maxima, does not change.
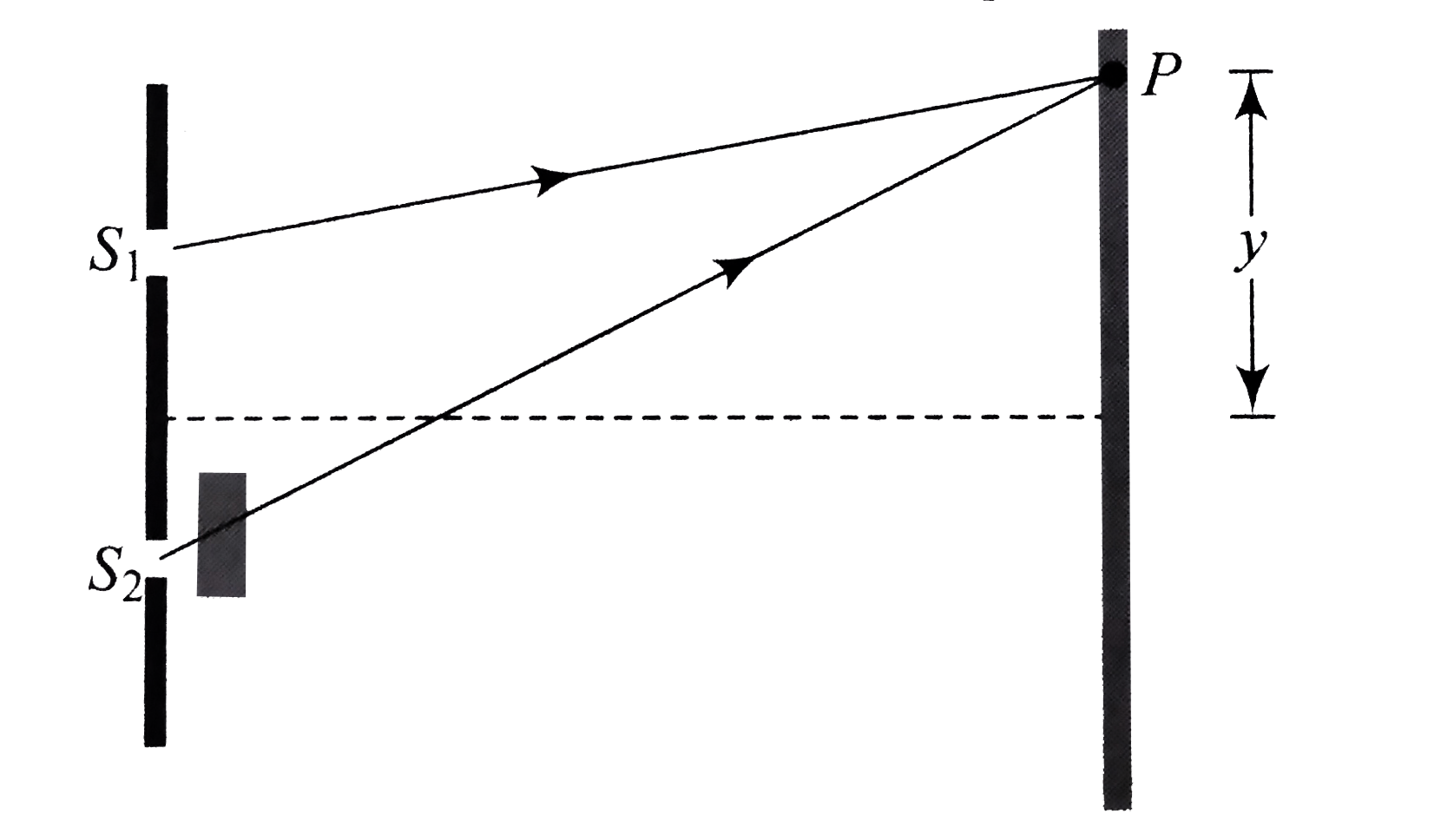
The value of η isView Solution
