In Fig. 6, l and m are two parallel tangents to a circle with centre O, touching the circle at A and B respectively. Another tangent at C intersects the line at D and in at E. Prove that ZDOE=90.
a3R2b
a3Rb
a3R6b
a3R3b
The correct Answer is:C
Given, Q=at−bt2∴I=dQdt=a−2bt
At t=0,Q=0⇒I=0
Also, I=0 at t=a/2b
∴ Total heat produced in resistance R,
H=a/2b∫0I2Rdt=Ra/2b∫0(a−2bt)2dt
=Ra/2b∫0(a2+4b2t2−4abt)dt
=R[a2t+4b2t33−4abt22]a/2b0
=R[a2×a2b+4b23×a38b3−4ab2×a24b2]=a3R6b
Topper's Solved these Questions
- BOOK - MTG GUIDECHAPTER - CURRENT ELECTRICITY EXERCISE - CHECK YOUR NEET VITALS16videos
CURRENT ELECTRICITY
- BOOK - MTG GUIDECHAPTER - ATOMS AND NUCLEIEXERCISE - AIPMT/NEET(MCQs)40videos
ATOMS AND NUCLEI
- BOOK - MTG GUIDECHAPTER - DUAL NATURE OF MATTER AND RADIATION EXERCISE - AIPMT/ NEET MCQs30videos
DUAL NATURE OF MATTER AND RADIATION
Similar Questions
landm are two parallel tangents to a circle with centre O, touching the circle at A and B respectively. Another tangent at C intersects the line l at D and m at E. Prove that∠DOE=90∘.
View SolutionPA and PB are tangents to the circle with centre O touching it at A and B respectively. IF ∠APO=25∘ , then ∠POB is
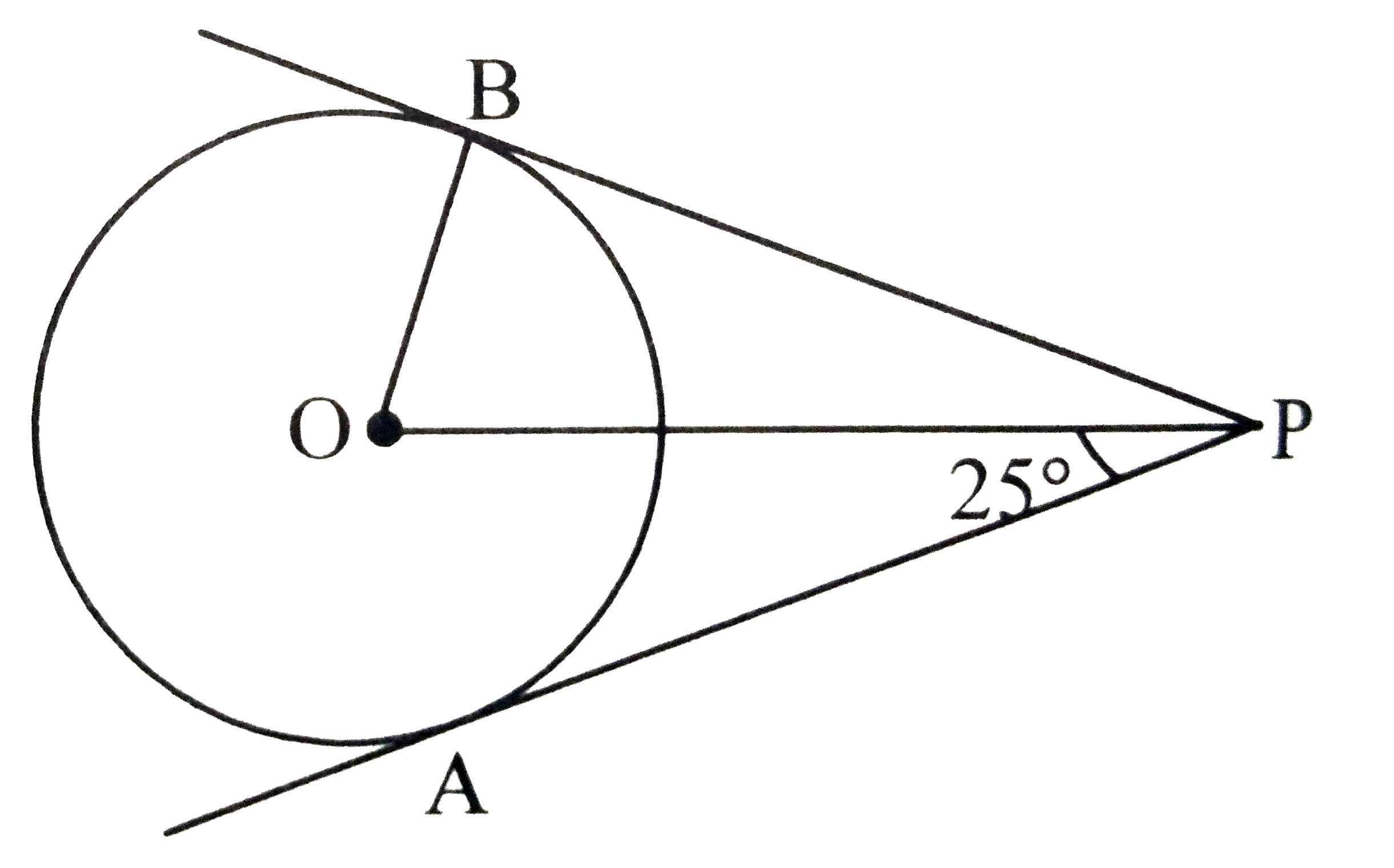 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
PQ and RS are two parallel tangents to a circle with centre O and another tangent AB wih point of contact C intersect PQ at A and RS at B. then find ∠AOB
A60∘B120∘C90∘D180∘
XYand X'Y'are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XYat A and X'Y'at B. Prove that ∠AOB = 90o
View SolutionIn Fig XY and X'Y' are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY and X'Y' at B , prove that ∠AOB=90∘
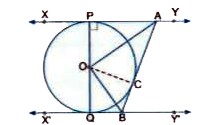 View Solution
View SolutionPA and PB are tangents to the circle with centre O from an external point P, touching the circle at A and B respectively. Show that the quadrilateral AOBP is cyclic.
View SolutionIf TP and TQ are the two tangents to a circle with centre O so that ∠POQ=110∘, then ∠PTQ is equal to
View SolutionIn Fig , XP and XQ are two tangents to the circle with centre O , drawn from an external point X . ARB is another tangent, touching the circle at R . Prove that XA + AR = XB + BR.
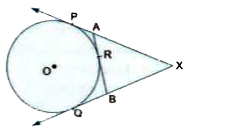 View Solution
View SolutionCP and CQ are tangents to a circle with centre O. ARB is another tangent touching the circle at R. If CP = 11 cm, BC = 7cm, Then the length BR is :
View SolutionIn Fig. 10.74, CP and CQ are tangents to a circle with centre O . ARB is another tangent touching the circle at R . If CP=11cm and BC=7cm , then find the length of BR . (FIGURE)
View Solution

