In fig. mass m is being pulled on the incline of a wedge of mass M. All the surfaces are smooth. Find the acceleration of the wedge.

Method 1: Let the acceleration of wedge be a rightward. Then acceleration of wedge be a rightward. Then acceleration of block relative to wedge will aslo be a, but down in incline. Hence the net acceleration of the block will be equal to the vector sum of these two as shown in fig.
(→am)x=(→amM)x+(→am)x
(→am)x=acosθ+a=−a(1+cosθ)
(→am)y=(→amM)y=asinθ+0=asinθ
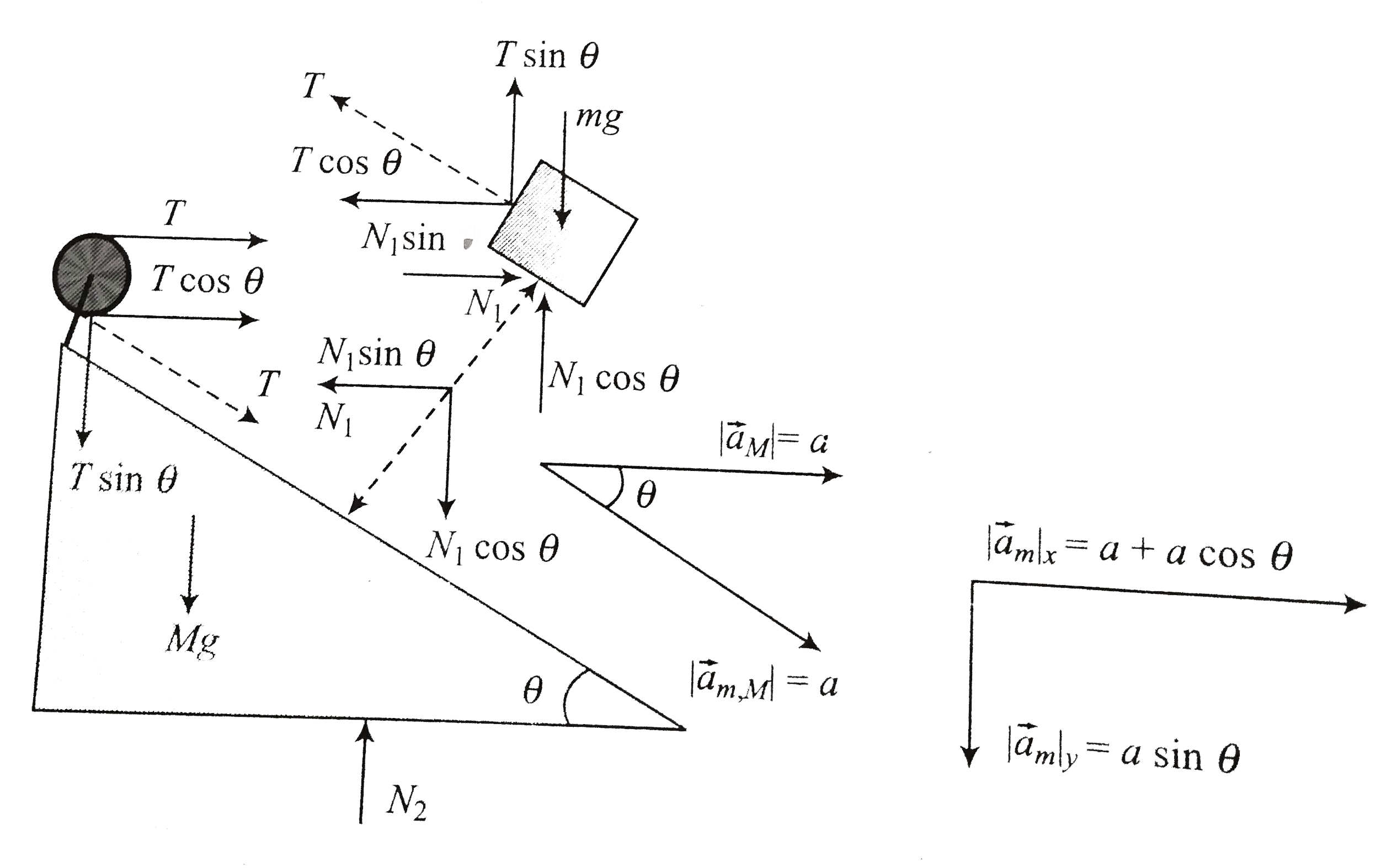
Now considering FBDs.
For the wedge: N2=N1cosθ+Tsinθ+Mg...(i)
T+Tcosθ−Tsinθ=masinθ=Ma (ii)
For the block:
N1sinθ−Tcosθ=m(a+acosθ)...(iii)
mg−N1cosθ−Tsinθ=masinθ..(iv)
from (iii), N1=Tcosθ+m(a=acosθ)sinθ
Putting the value of N1 in (iv)
mg−cosθsinθ(Tcosθ+m(a+acosθ))−Tsinθ=masinθ
Simplify to get T=mgsinθ−ma(1+cosθ) (v)
From (ii) and (iii), T=Ma+m(a+acosθ) (iv)
Solving (v) and (vi), we get a=mgsinθM+am(1+cosθ)
Method 2: The acceleration of wedge and block will be same in a direction perpendicular to the incline of wedge which is a sinθ
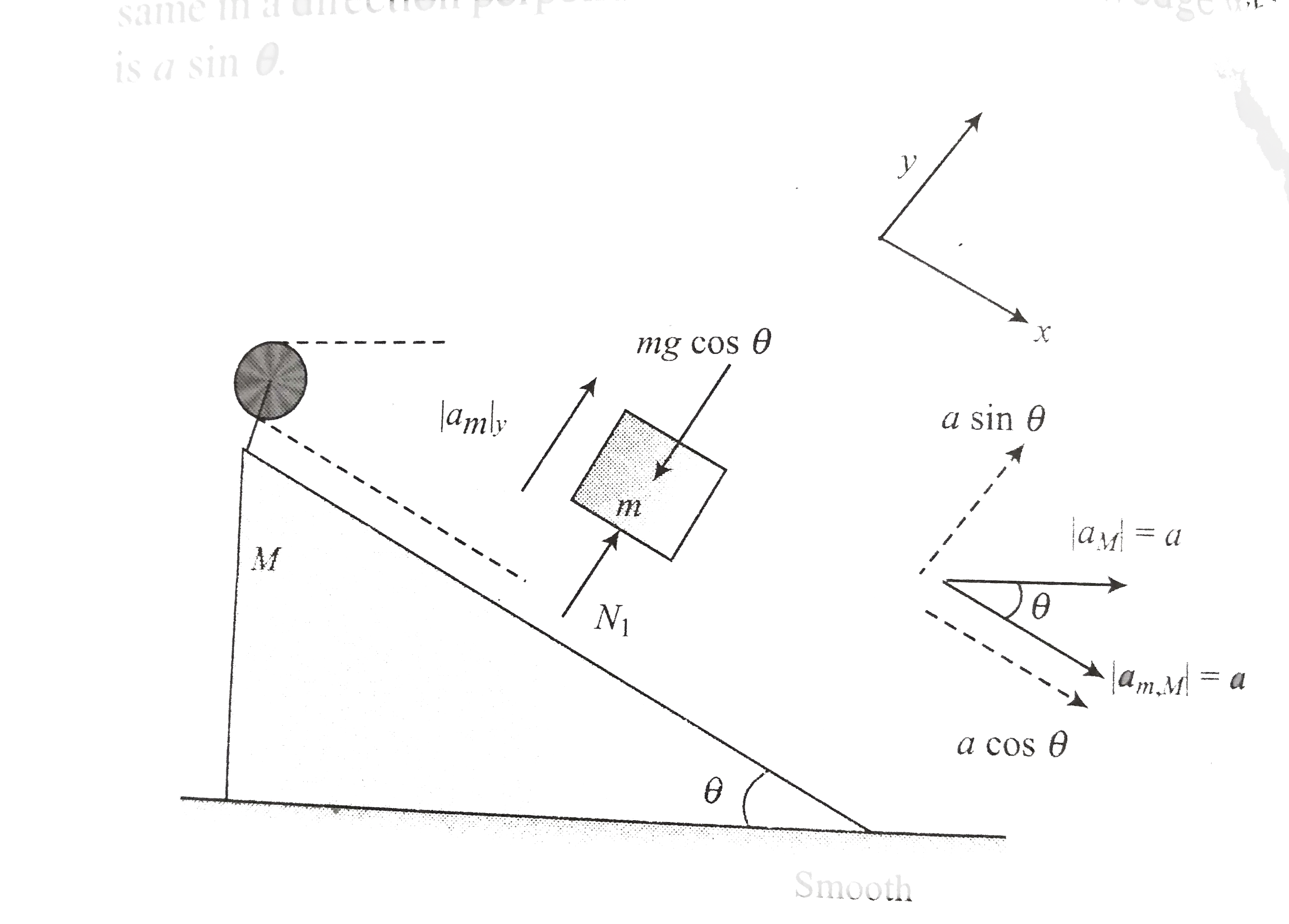
Writing the equation of block for this direction, we get
N1−mgcosθ=masinθ..(viii)
Now solving (ii), (iii) and (iv) we get the same answer as earlier.
Method 3: If we consider block and wedge as a system, then the only horizontal force acting on the system is tension in the string as shown in fig.
Writing the equation for the combined system in horizontal direction, we get
T=Ma+m(a+acosθ) ...(viii)
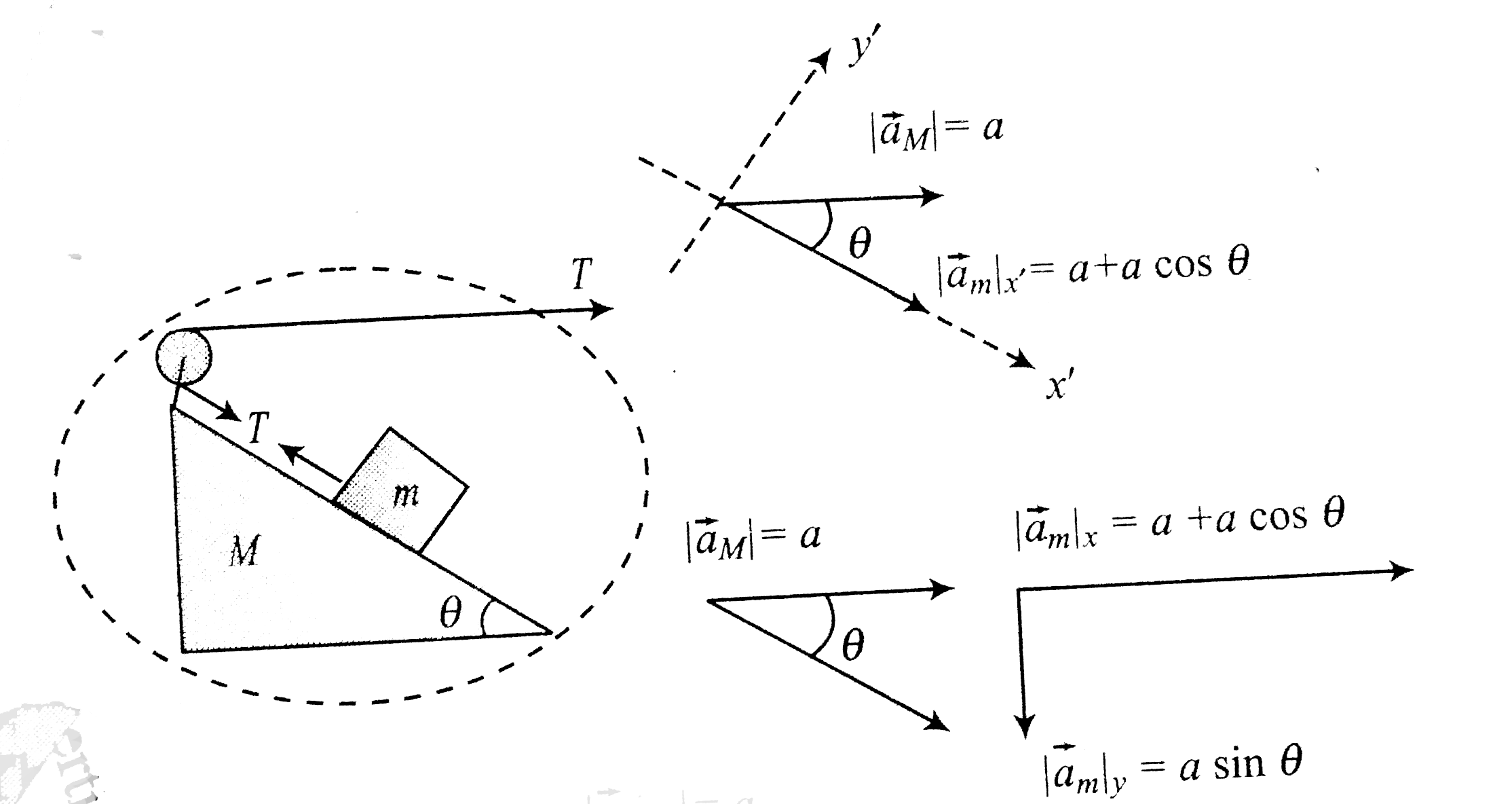
Consider the motion of block parallel to sloping surface, and writing the equation of motion w.r.t. ground
(→am_(x'))=(→am,M)+(→aM)x'=aacosθ
mgsinθ−T=m(a+acosθ)
T=mgsinθ−m(a+acosθ)...(ix)
Solving (viii) and (ix), we get
a=mgsinθM+2m(1+cosθ)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.111videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.235videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer5videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
Similar Questions
In the Fig. shown, mass 'm' is being pulled on the incline of a wedge of mass M. All the surface are smooth. Find the acceleration of the wedge.
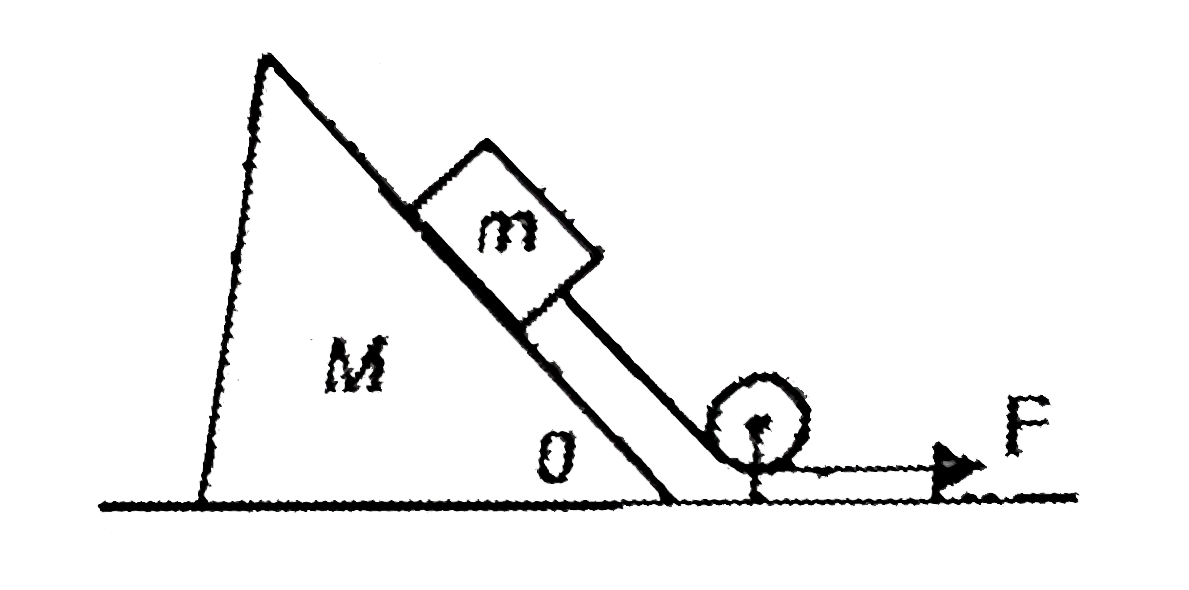 View Solution
View SolutionIn the arrangement shown in figure, the rod of mass m held by two smooth walls, remains always perpendicular to the surface of the wedge of mass M. Assuming all the surface to be frictionless, find the acceleration of the rod and that of the wedge.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
All surfaces are smooth. The acceleration of mass m relative to the wedge is
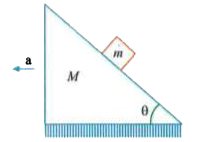 AgsinθBgsinθ+acosθCgsinθ−acosθDacosθ
AgsinθBgsinθ+acosθCgsinθ−acosθDacosθ - Question 2 - Select One
All surfaces are smooth The acceleration of mass m relative to the wedge is
 .AgsinθBgsinθ+acosθCgsinθ−acosθDacosθ
.AgsinθBgsinθ+acosθCgsinθ−acosθDacosθ - Question 3 - Select One
All the surfaces are smooth as shown in figure. The acceleration of mass m relative to wedge is :
 Ag sin θBg sin θ + a cos θCg sin θ - a cos θDa cos θ
Ag sin θBg sin θ + a cos θCg sin θ - a cos θDa cos θ
Figure-2.54 shows a block of mass m is placed on an inclined wedge of mass M If the system is released from rest find the acceleration of m and M.
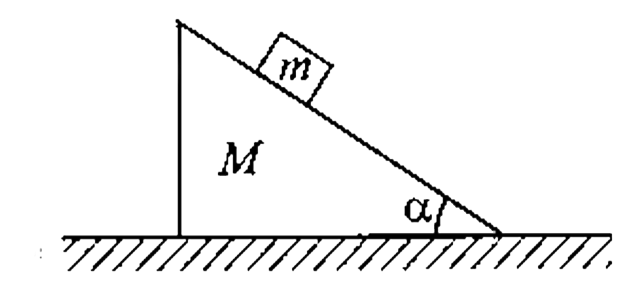 View Solution
View SolutionA block of mass m is placed on the inclined sufrace of a wedge as shown in fig. Calculate the acceleration of the wedge and the block when the block is released. Assume all surfaces are frictionless.
 View Solution
View SolutionA block of mass M is connected with a particle of mass m by a light inextensible string as shown in fig. Assuming all contaction surfaces as smooth, find the acceleration of the wedge after releasing the system.
 View Solution
View SolutionIn the arrangement shown in figure, the rod of mass mhelp by two smooth walls, remains always perpendicular to the surface of the wedge of mass M. Assuumming all the surface to be frictionless, find the acceleration of the rod and that of the wedge.
 View Solution
View SolutionIn the arrangement shown in figure wedge of mass M moves towards left with an acceleration a. All surfaces are smooth. The acceleration of mass m relative to wedge is
 View Solution
View Solution

