In figure, the light spring is of force constant k and is on a smooth horizontal surface. Initially the spring is relaxed. Calculate the work done by an external agent to lower the hanging body of mass M slowly, till it remains in equilibrium.
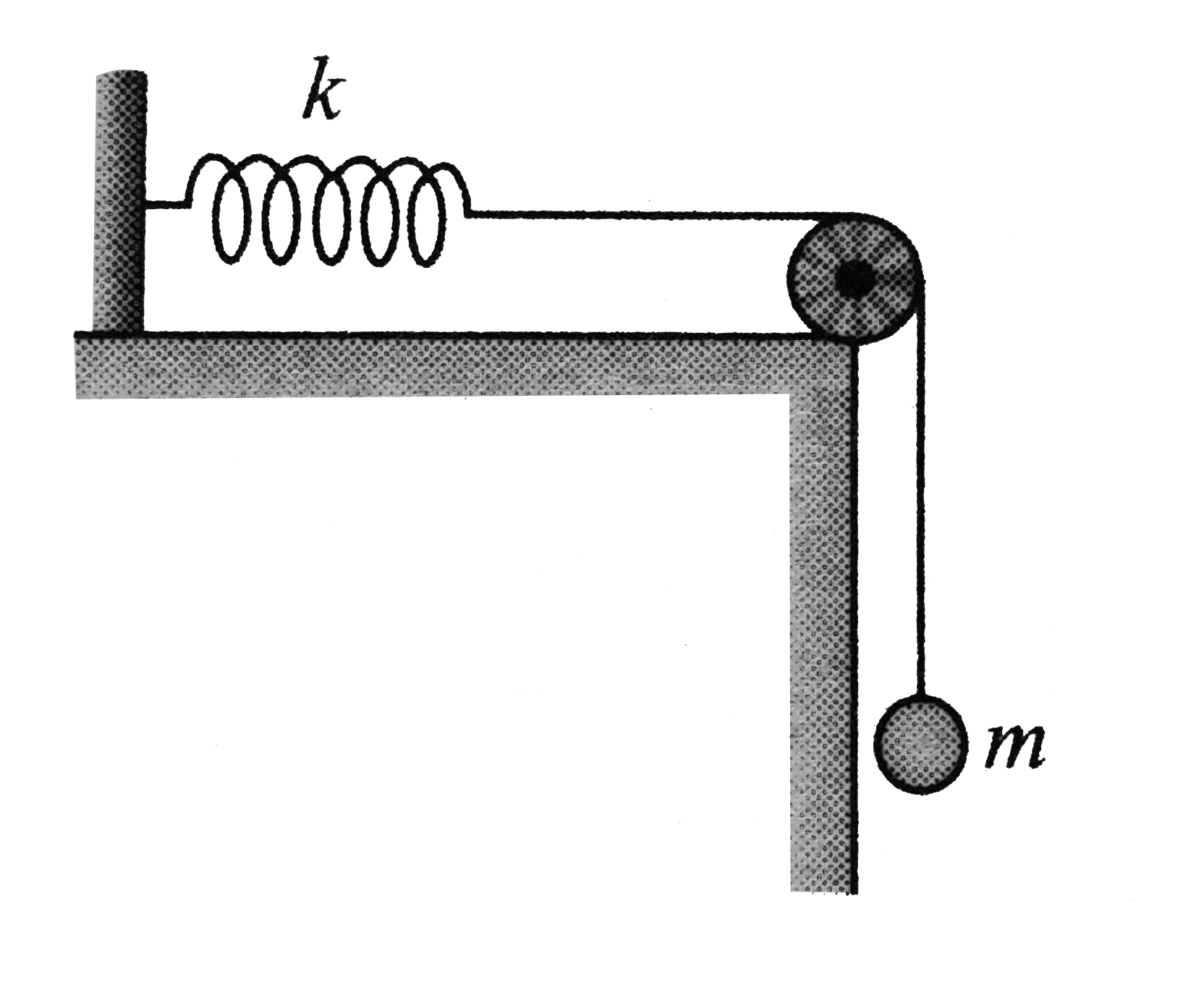
The correct Answer is:m2g2−2k
Let the force applied by the man, the external agent, be F. The net force acting on the body is zero because it is lowered slowly.
Let the elongation of the spring at any instant be x.
Thus the spring pulls the body up by an amount kx.
⇒Fnet=F+kx−mg=0
⇒F=mg−kx (i)
The work done dW by F in lowering the body through a distance x0 is
W=∫dW=x0∫0(mg−kx)dx
⇒W=mgx0−12kx20

The body is lowered (slowly) till it remains in equilibrium. Therefore the external force F is variable and it is zero at the equilibrium of m, since the spring force kx0 counter balances the weight mg of the body
⇒kx0=mg⇒x0=mgk (iii)
Putting x0=mgk= in Eqs. (ii), we obtain W=m2g2−2k
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Single Correct
100 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.5
15 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
Find the work done by an external agent in lowering a block of mass m slowly on a light of stiffness k, till it comes to rest.
View SolutionTwo blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View Solution
Knowledge Check
The work done by external agent in stretching a spring of force constant k from length l1 to l2is
Ak(l22−l21)B12k(l22−l21)Ck(l2−l1)D12k(l2+l1)A block of mass m is attached to a spring of force constant k whose other end is fixed to a horizontal surface. Initially the spring is in its natural length and the block is released from rest. The average force acting on the surface by the spring till the instant when the block has zero acceleration for the first time is
 AmgπB2mgπC3mgπD4mgπ
AmgπB2mgπC3mgπD4mgπWork done by the gravitational force on a body of mass ''m'' moving on a smooth horizontal surface through a distance 's' is
AmgsB−mgsC0D2mgs
A block of mass M is tied to a spring of force constant k and placed on a smooth horizontal surface. The natural length of the spring is L. P is a point on the spring at a distance L4 from its fixed end. The block is set in oscillations with amplitude A. Find the maximum speed of point P on the spring.
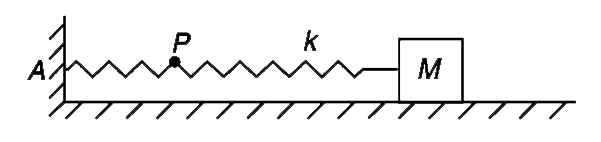
View SolutionA block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unsrtretched when a constnt force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View SolutionA small mass m is moved slowly from the surface of the earth to a height h above the surface. The work done (by an external agent) in doing this is
View SolutionA small mass m is moved slowly from the surface of the earth to a height h above the surface. The work done (by an external agent) in doing this is
View SolutionA small mass m is moved slowly from the surface of the earth to a height h above the surface. The work done ( by an external agent) in doing this is
View Solution
