In the above problem if body is thrown down with velocity 'u' the equation for the descent time is
h=12gt2
h=ut+12gt2
−h=−ut+12gt2
−h=−ut+12gt2
The correct Answer is:B
To solve the problem of finding the descent time when a body is thrown down with an initial velocity 'u', we can use the equations of motion under uniform acceleration due to gravity. Here’s the step-by-step solution:
Step 1: Understand the problem
When a body is thrown downward with an initial velocity 'u', it is subject to gravitational acceleration 'g' (approximately 9.81 m/s²). We need to find the time 't' it takes for the body to descend a certain distance 's'.
Step 2: Write the equation of motion
The equation of motion that relates initial velocity, acceleration, distance, and time is given by:
s=ut+12gt2
Where:
- s = distance traveled
- u = initial velocity (downward)
- g = acceleration due to gravity (approximately 9.81 m/s²)
- t = time of descent
Step 3: Rearrange the equation
To find the time 't', we need to rearrange the equation. This is a quadratic equation in the form of:
12gt2+ut−s=0
Step 4: Apply the quadratic formula
Using the quadratic formula t=−b±√b2−4ac2a, we identify:
- a=12g
- b=u
- c=−s
Substituting these values into the quadratic formula gives:
t=−u±√u2−4⋅12g⋅(−s)2⋅12g
Step 5: Simplify the expression
This simplifies to:
t=−u±√u2+2gsg
Step 6: Choose the correct root
Since time cannot be negative, we take the positive root:
t=−u+√u2+2gsg
Final Answer
Thus, the equation for the descent time when a body is thrown down with an initial velocity 'u' is:
t=−u+√u2+2gsg
---
When a body is thrown downward with an initial velocity 'u', it is subject to gravitational acceleration 'g' (approximately 9.81 m/s²). We need to find the time 't' it takes for the body to descend a certain distance 's'.
The equation of motion that relates initial velocity, acceleration, distance, and time is given by:
s=ut+12gt2
Where:
- s = distance traveled
- u = initial velocity (downward)
- g = acceleration due to gravity (approximately 9.81 m/s²)
- t = time of descent
To find the time 't', we need to rearrange the equation. This is a quadratic equation in the form of:
12gt2+ut−s=0
Using the quadratic formula t=−b±√b2−4ac2a, we identify:
- a=12g
- b=u
- c=−s
t=−u±√u2−4⋅12g⋅(−s)2⋅12g
This simplifies to:
t=−u±√u2+2gsg
Since time cannot be negative, we take the positive root:
t=−u+√u2+2gsg
Thus, the equation for the descent time when a body is thrown down with an initial velocity 'u' is:
t=−u+√u2+2gsg
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - EXERCISE -II
80 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - PRACTICE EXERCISE
58 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question
15 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-III
49 Videos
Similar Questions
In the above problem, what is the component of its velocity perpendicular to the plane when it strikes at A ?
View SolutionA ball is thrown vertically upwards from the top of tower of height h with velocity v . The ball strikes the ground after time.
View SolutionWhen a body is thrown up in a lift with a velocity u relative to the lift, the time of flight is found to be t. The acceleration with which the lift is moving up is
View SolutionIn the above problem the angular velocity of the system after the particle sticks to it will be?
View SolutionA stone thrown upward with a speed u from the top of a tower reaches the ground with a velocity 4u. The height of the tower is
View SolutionA body is thrown vertically up with certain initial velocity, the potential and kinetic energies of the body are equal is thrown with double the velocity upwards, the ratio of potential and kinetic energies upwards, the ratio of potential and kinetic energies of the body when it crosses the same point, is
View SolutionFrom the top of a tower body A is thrown up vertically with velocity u and another body B is thrown vertically down with the same velocity u.If VA and VB are their velocities when they reach the ground and tA and tB are their times of flight ,then
View SolutionA body is thrown horizontally with a velocity of v m/s from the top of a tower of height 2h reaches the ground in 't' seconds. If another body double the mass is thrown horizontally with a velocity 5v m/s from the top of another tower of height 8h. In the above problem if the first reaches the ground at a horizontal distance 'x' the second body reaches the ground at a horizontal distance
View SolutionA body is thrown horizontally with a velocity of v m/s from the top of a tower of height 2h reaches the ground in 't' seconds. If another body double the mass is thrown horizontally with a velocity 5v m/s from the top of another tower of height 8h it reaches the ground in a time of
View SolutionThe displacement-time graph of a body is shown in.
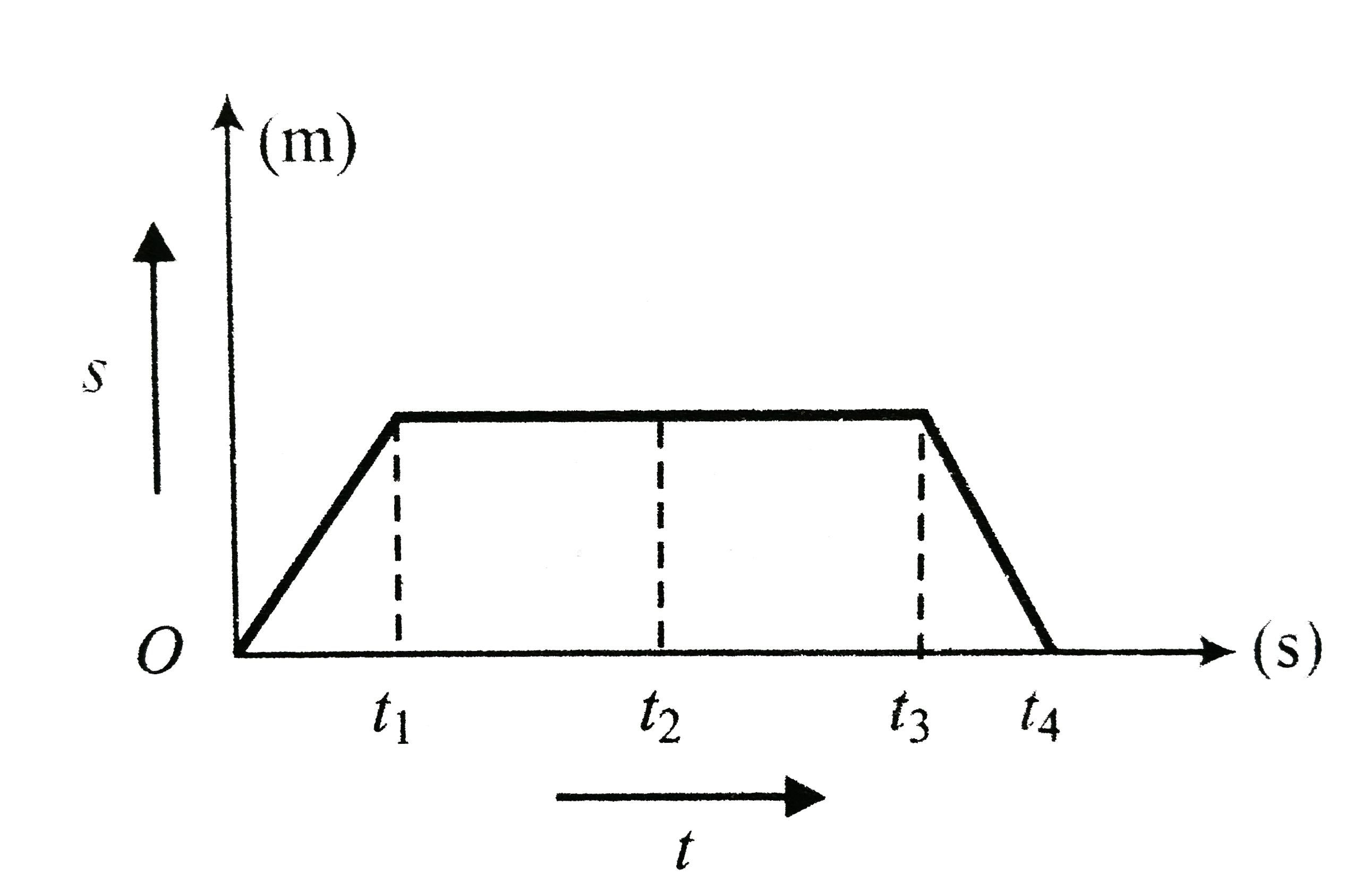 .
.
The velocity-time graph of the motion of the body will be .
View Solution
