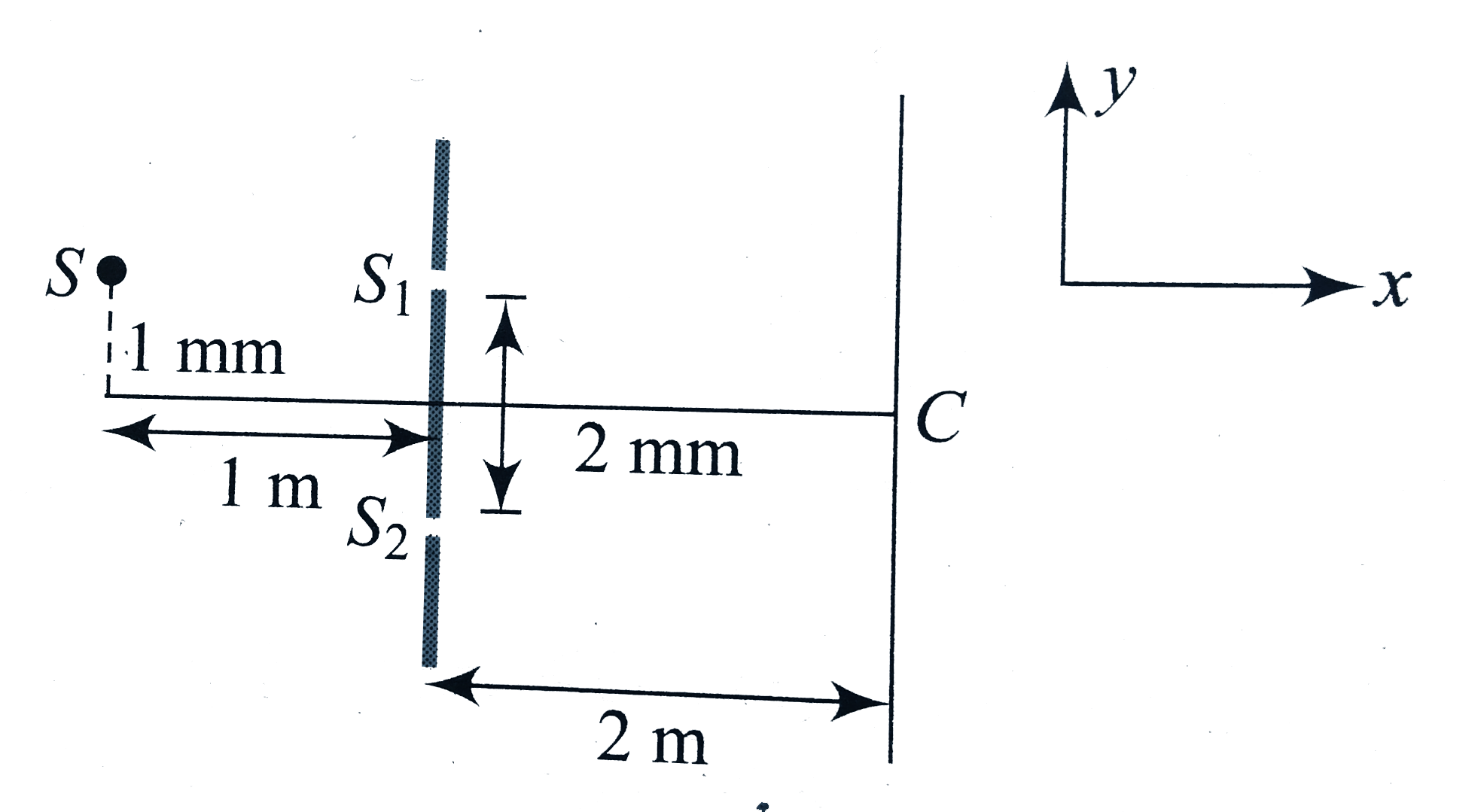
In the arrangement shown in figure, light of wavelength 6000Å is incident on slits S1 and S2 have been opened such that S3 is the position of first maximum above the central maximum and S4 is the closest position where intensity is same as that of the ligth used, below the central maximum Point O is equidistant from S1 and S2 and O' is equidistant from S3 and S4. Then intensity of inciden light is I0
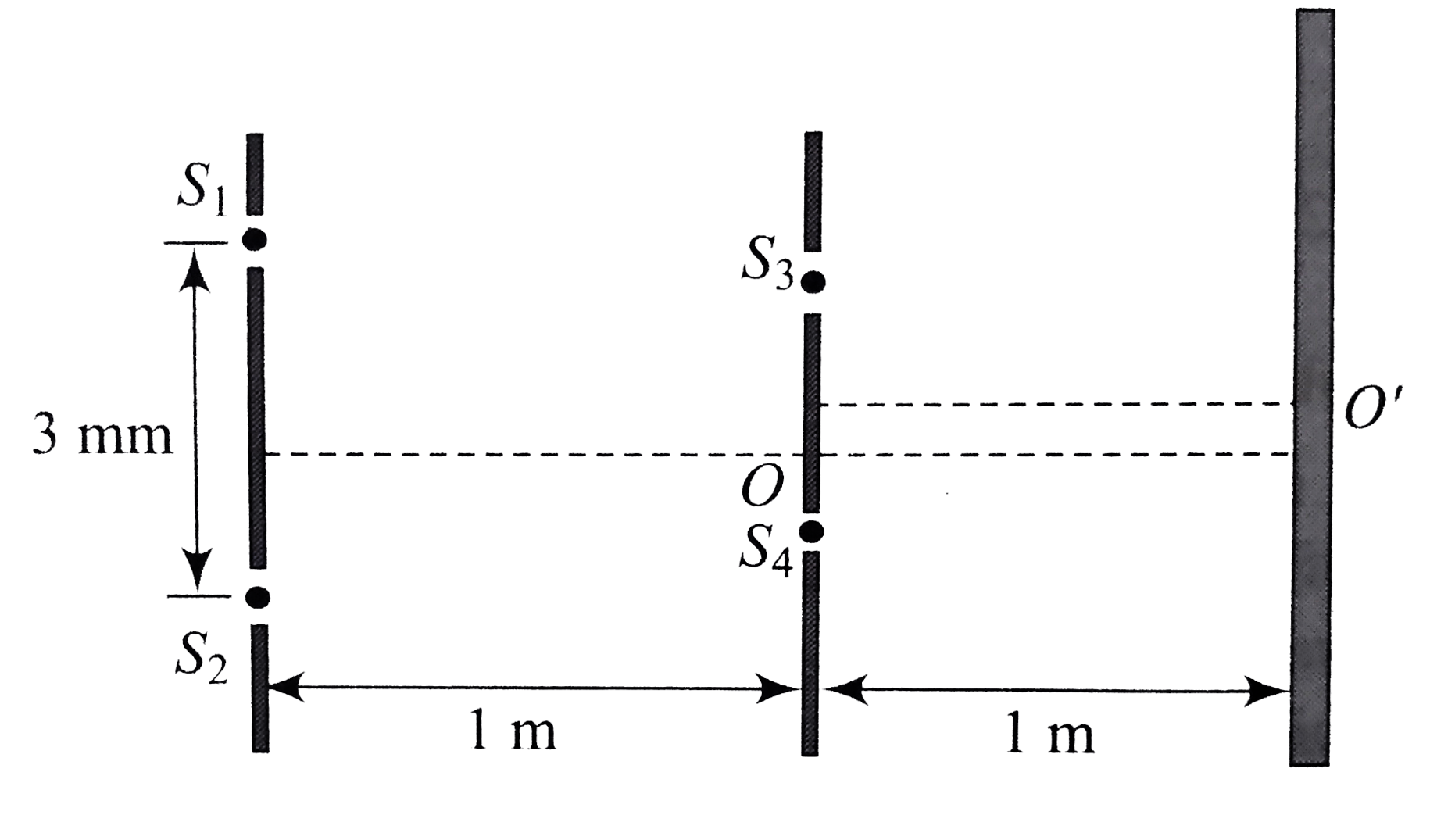
Find the intensity at O' (on the screen).
4.5I0
3I0
2I0
5I0
The correct Answer is:b
From the given condition,
OS3=Dλd=1×6×10−73×10−3=2×10−4m
Let the reaching from S1 and S2 to S4 and phase difference ϕ and intensity of incident light is I0. Resultant intensity at S4 is
(i) I=4I0cos2(ϕ2)
As I=I0, hence
I04I0=cos2(ϕ2)
⇒cos(ϕ2)=12=cos60∘
(ii) ϕ=2π3,ϕ=2π3Δx⇒Δx=λ3
(iii) As Δx=λ3 , using Δxd=yD
y=ΔxDd⇒OS4=Dλ3d
Therefore, S3S4=OS3+OS4=43dλd=83×10−4m
Now, resultant wave coming out of S3 has intensity 4I0 and waves coming out of S4 have intensity I0.
Phase difference at S3=2π
Phase difference at S4=2π/3
These phase diffference ara ralative to the ligth incident on slit S1 and S2.
Now, S3 and S4 are secondary sources of ligth.
Phase difference at O' =4π/3, equal to inital phase difference between the ligth reaching at O', i.e.,
2π2π3=4π3
Let intensity at O' be I'. Then
I'=I0+4I0+2√I0√4I0cos(4π3)
=5I0+4I0cos(π+π3)=3I0
For the brightest fringe, phase difference =2np,n=0,±1,±2,...
Let I'' be the intensity of the brightest fringe.
I''=I0+4I0+2√I0√4I0cosϕ (where cosϕ=1).
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Integer3videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Archives4videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assertion- Reasoning13videos
WAVE OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type12videos
SOURCES OF MAGNETIC FIELD
Similar Questions
In the arrangement shown in figure, light of wavelength 6000Å is incident on slits S1 and S2 have been opened such that S3 is the position of first maximum above the central maximum and S4 is the closest position where intensity is same as that of the ligth used, below the central maximum Point O is equidistant from S1 and S2 and O' is equidistant from S3 and S4. Then intensity of inciden light is I0
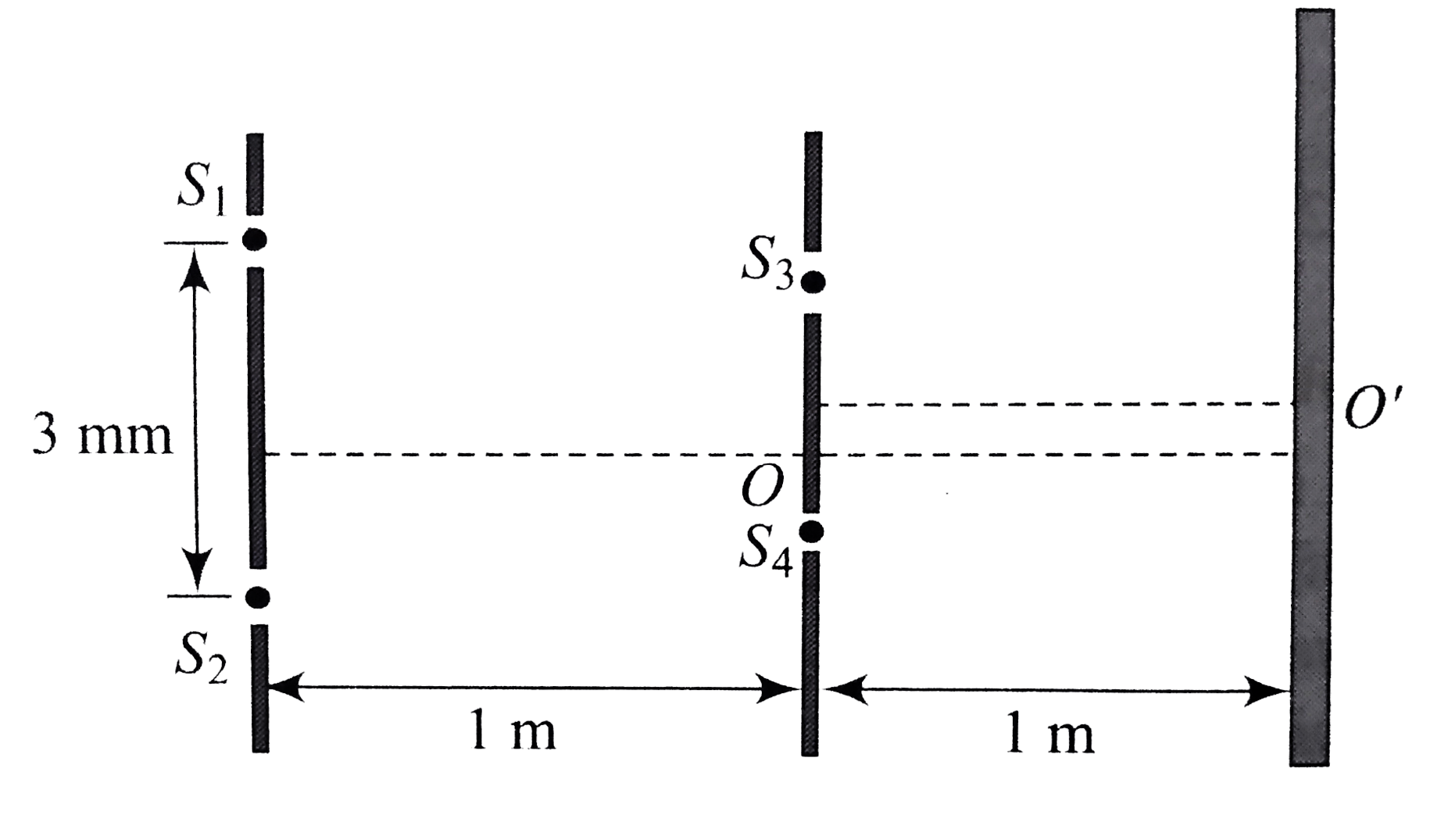
Find the intensity of the brightest fringe.View SolutionLight wavelength 6000 Å is incident normally on a slit of width 24×10−5 cm. find out the angular position of seconds minimum from central maximum?
View SolutionIn a Young's double-slit experiment set up, source S of wavelength 6000Å illuminates two slits S1 and S2 which act two coherent sources. The sources S oscillates about its shown position according to the eqation y=1+cosπt, where y is in millimeter and t in second.
At t=2 s, the position of central maxima isView SolutionIn the circuit shown in the figure, if switches S1 and S2 have been closed for a long time, then charge on the capacitor.
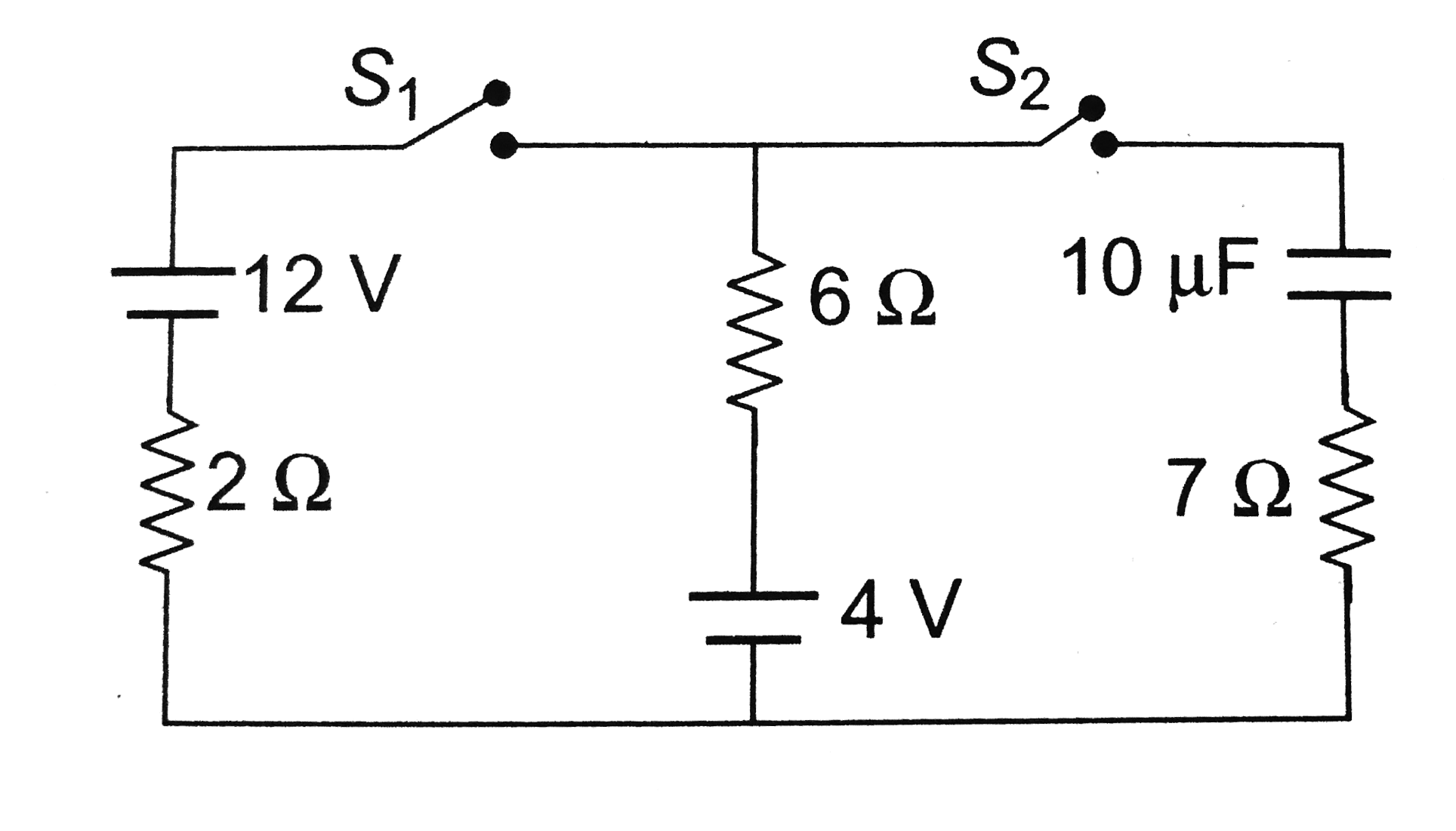 View Solution
View SolutionIn the set up shown in figure, the two slits S1 and S2 are not equidistant from the slit S. The central fringe at O is then
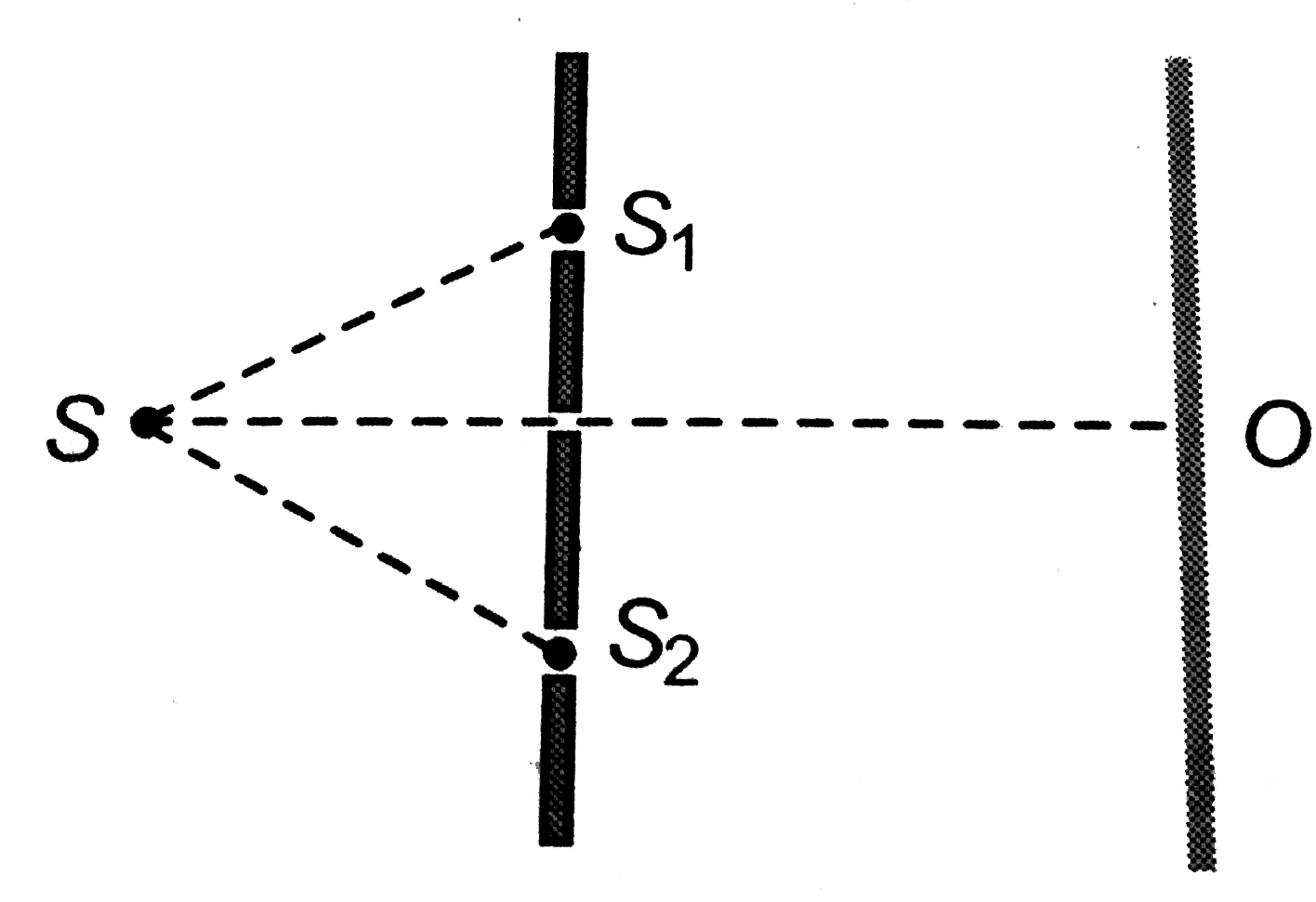 View Solution
View SolutionIn fig., light of wavelength λ=5000Å is incident on the slits (in a horizontally fixed place).
Here, d=1mm and D=1m
Take origin at O and XY plane as shown in the figure. The screen is released from rest from the initial position as shown
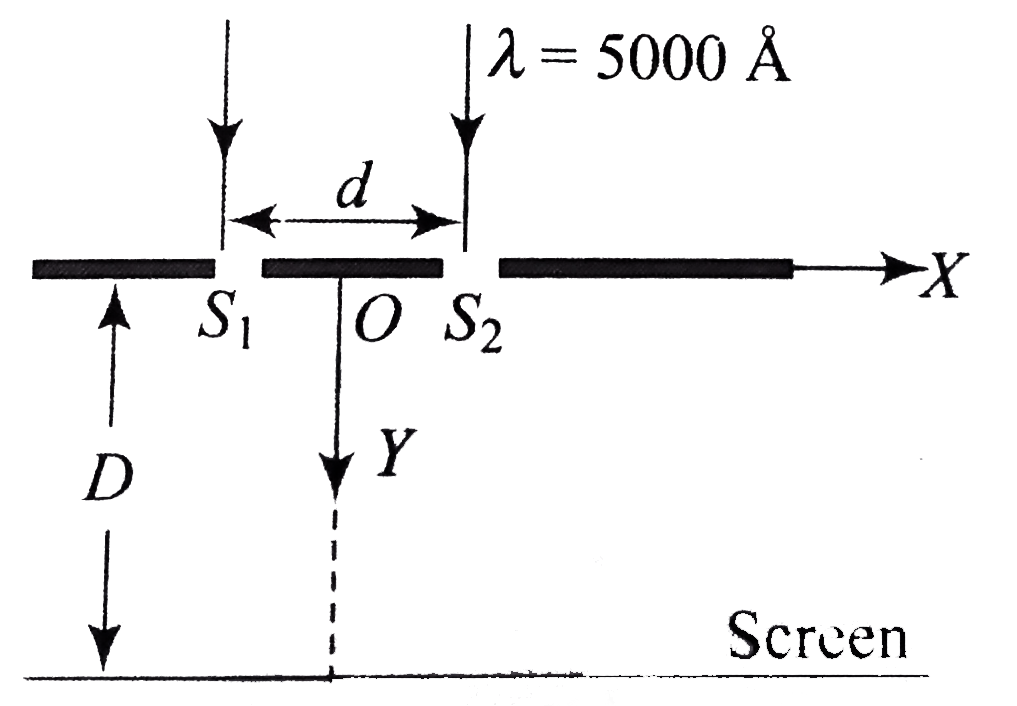
The velocity of central maxima at t=5s isView SolutionIn arrangement shown in figure, plane wavefront of monochromatic light of wavelength λ is incident on identical slits S1 and S2. There is another pair of indentical slits S3 and S4 which are having separation Z=λD2d Point O is on the screen at the common perpendicular bisector of S1S2 and S3S4.I1 is the intensity at point O Now the board having slits S3S4 is moved upward parallel to itself and perpendicular to line AO till slit S4 is on line AO and it is observed that now intensity at point O is I2 then I2I1 is :
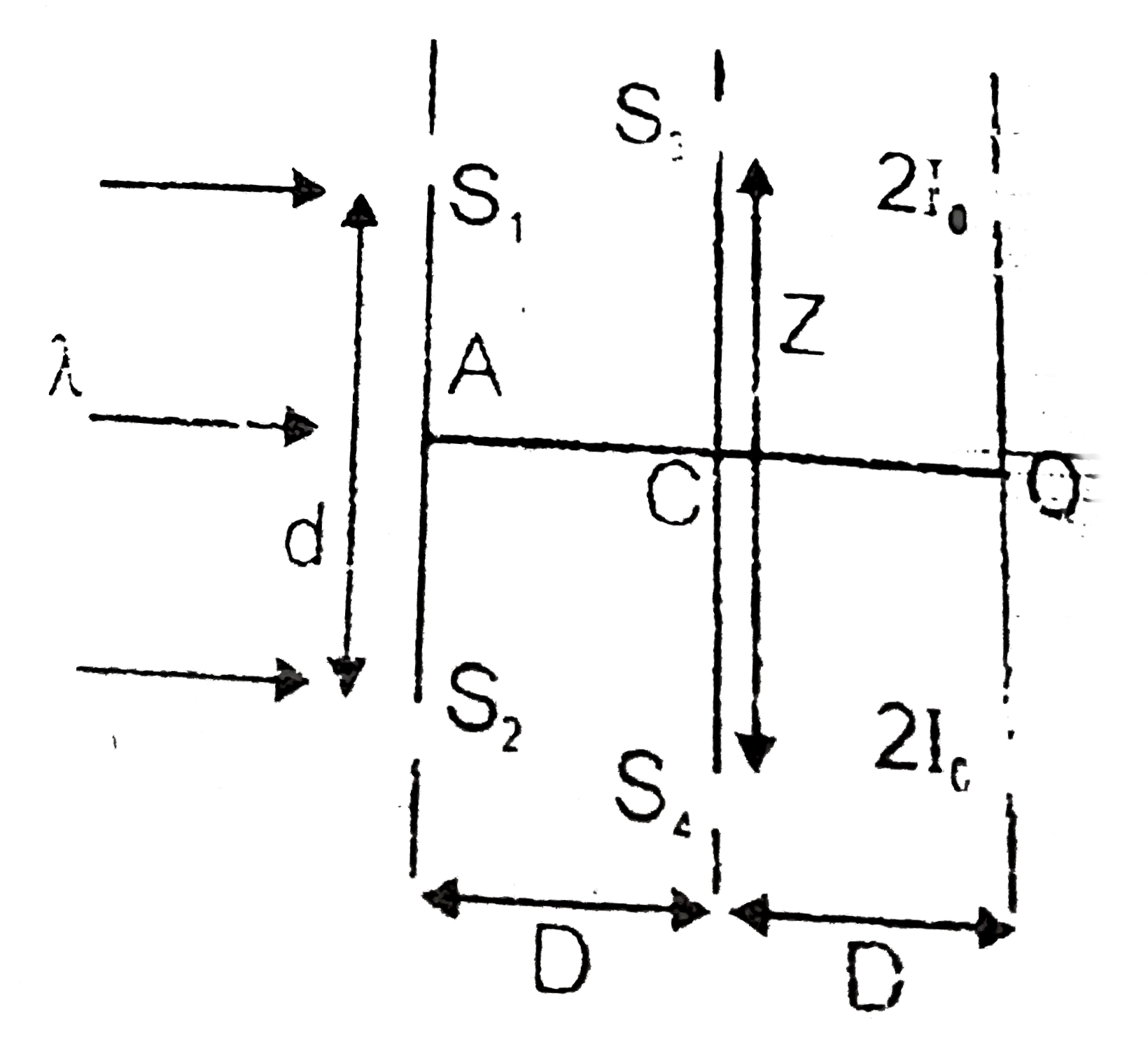 View Solution
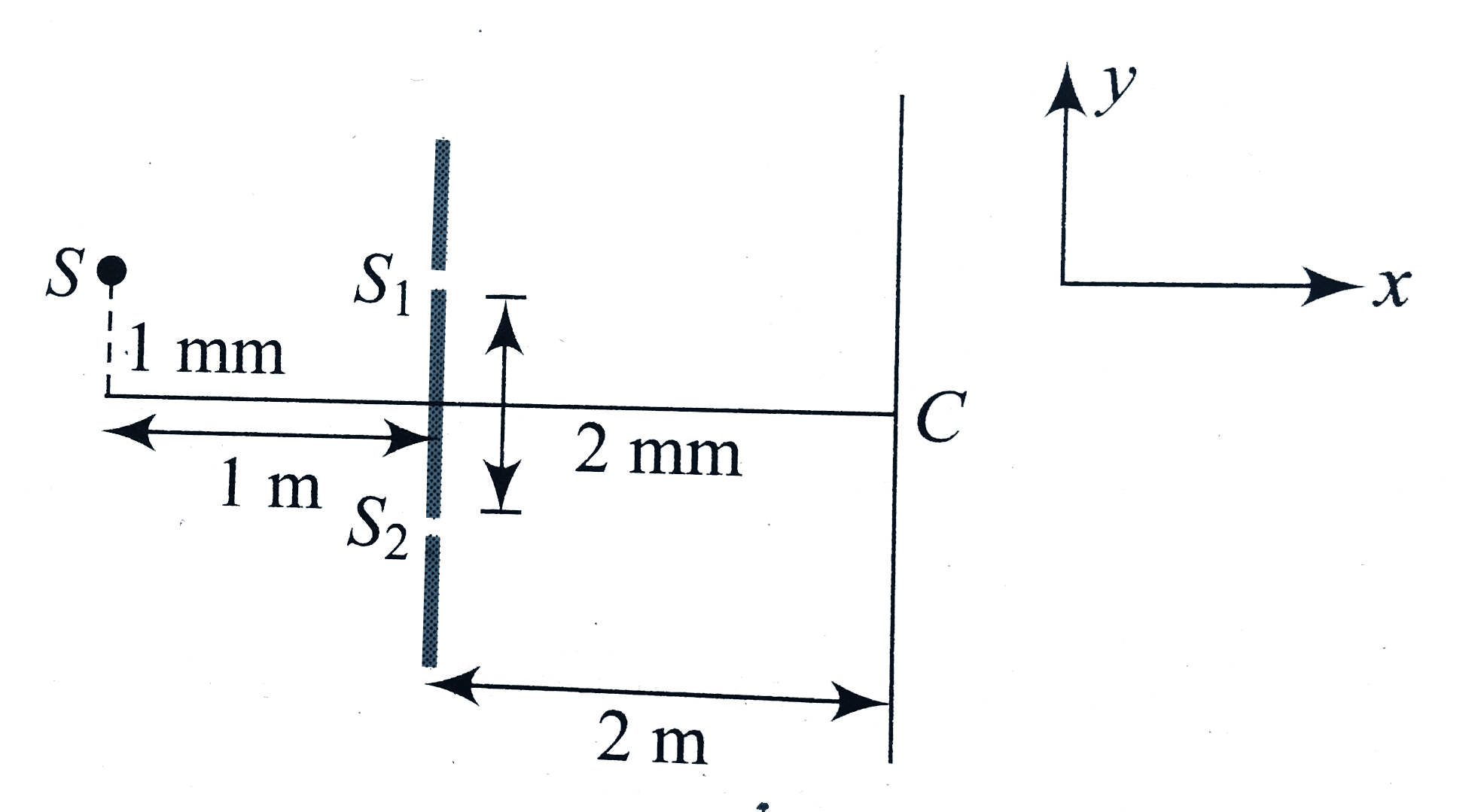
View SolutionIn the given figure ,C is middle point of line S1S2.A monochromatic light of wavelength γ is incident on slits.The ratio of intensites of S3andS4 is
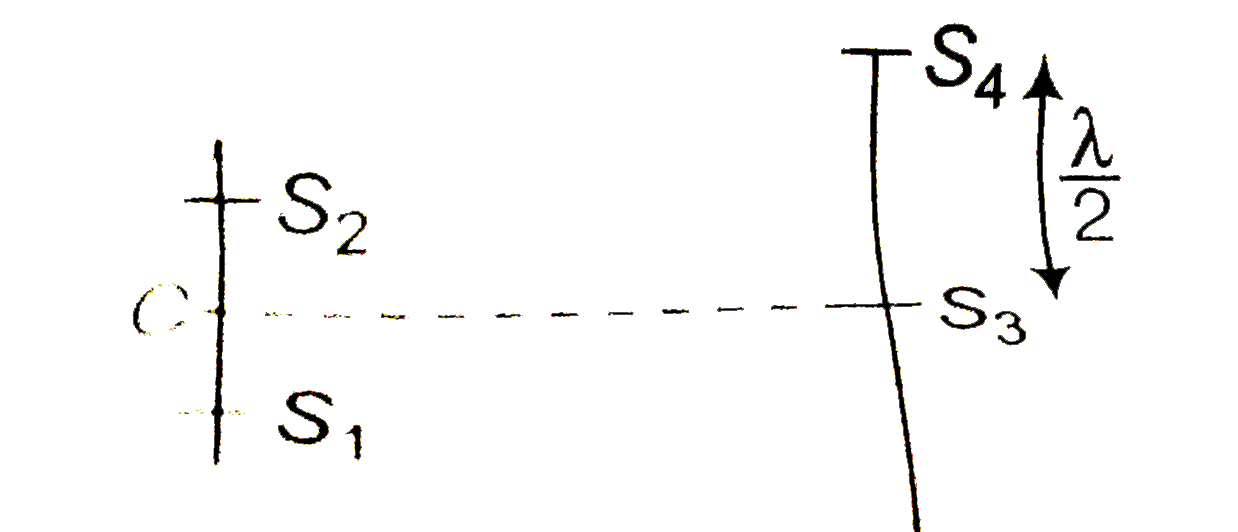 View Solution
View SolutionIn a Young's double-slit experiment set up, source S of wavelength 6000Å illuminates two slits S1 and S2 which act two coherent sources. The sources S oscillates about its shown position according to the eqation y=1+cosπt, where y is in millimeter and t in second.
At t=0, fringe width is β1, and at t=2 s, width of figure is β2. ThenView SolutionIn YDSE a=2mm, D = 2m, λ=500 nm. Find distance of point on screen from central maxima where intensity becomes 50% of central maxima
View Solution

