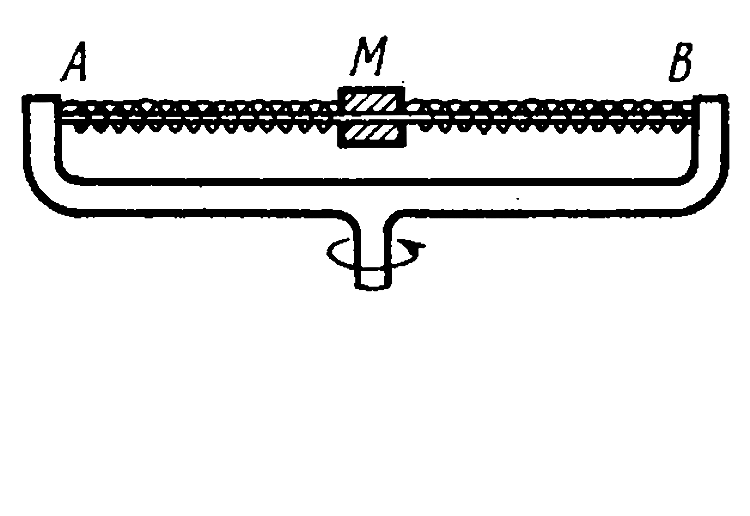
In the arrangement shown in figure the sleeve M of mass m=0.20kg is fixed between two identical springs whose combined stiffness is equal to x=20N/m. The sleeve can slide without friction over a horizontal bar AB. The arrrangement rotates with a constant angular velocity ω=4.4rad/s about a vertical axis passing through the middle of the bar . Find the period of small oscillations of the sleeve. At what values of ω will there be no oscillations of the sleeve ?
The correct Answer is:2π√mk−mω2
We will analyse se the problem relative to the rotating bar AB. As the acceleration of bar is centripetaing , a pseudo force will act on sleeve away from the centre and will be of magnitude m(ω2x).
If the sleves is displaced by x, net force towards center

F=kx−mω2x=(m−mω2)x
⇒period=2π√mk−mω2
Note that if k<mω2. there will be no oscillations of the sleves. It will rush to the point B if it is displaced slightly (for k<mω2). or will remain in the displaced position (fork=mω2).
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single Correct
107 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.2
23 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A particle of mass m is placed over a horizontal circular table rotating with an angular velocity ω about a vertical axis passing through its centre. The distance of the object from the axis is r. Find the force of friction f between the particle and the table.
View SolutionA sleeve A can slide freely along a smooth rod bent in the shape of a half-circle of radius R(figure). The system is set in rotation with a constant angular velocity ω about a vertical axis OO′. Find the angle θ corresponding to the steady position of the sleeve.
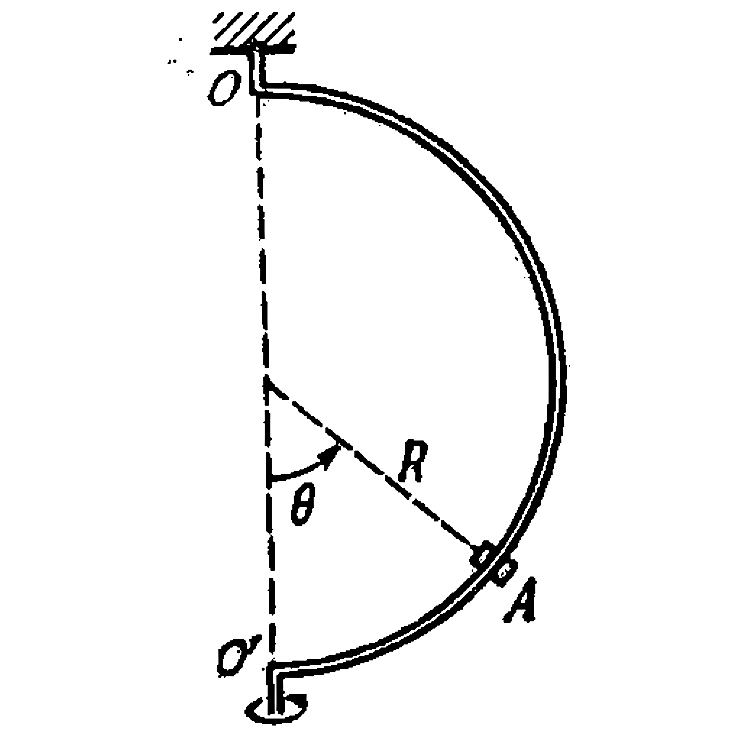
View Solution
Knowledge Check
In the arrangement shown, the sleeve of mass M is fixed between two identical springs whose combined force constant is k. The sleeve can slide without friction over a horizontal bar AB. The arragement rotates with a constant angular velocity ω about a vertical axis passing through the middle of the bar. the period of small oscillations of teh sleeve is.........
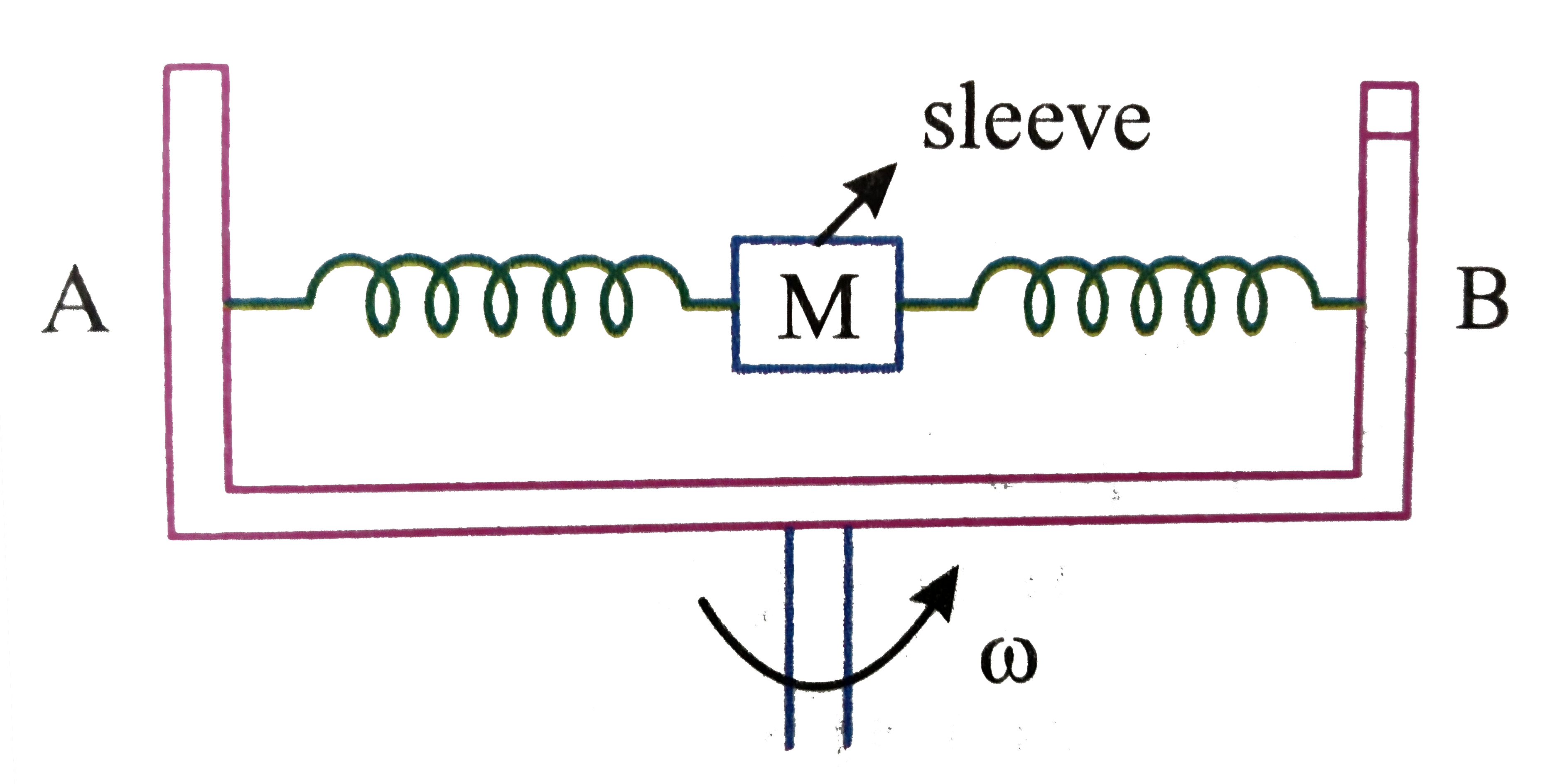 A2π√mkB2π√mk−mω2Cπ√mkDπ√mk−mω2
A2π√mkB2π√mk−mω2Cπ√mkDπ√mk−mω2A uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl]A copper ball of mass m=1kg with a radius of r=10cm rotates with angular velocity ω=2rad/s about an axis passing through its centre. The work should be performed to increase the angular velocity of rotation of the ball two fold is.
A1.2×10−2JB2.4×10−2JC3.6×10−2JD4.8×10−2J
A sleeve A can slide freely along a smooth rod bent in the shape of a half circle of radius R .The system is set in rotaion with a constant angular velocity ω about a vertical axis OO' .Find the angle θ corresponding to the steady position of the sleeve

View SolutionA small body of mass m=0.30kg starts sliding down from the top of a smooth sphere of radius R=1.00m. The sphere rotates with a constant angular velocity ω=6.0rad/s about a vertical axis passing through its centre. Find the centrifugal force of inertia and the Coriolis force at the moment when the body breaks off the surface of the sphere in the reference frame fixed to the sphere.
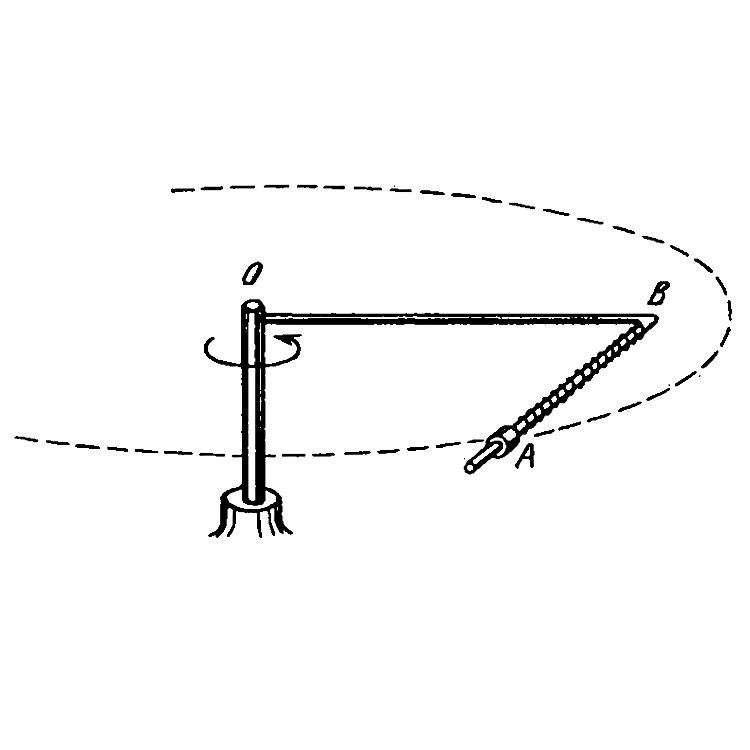
View SolutionA device (figure) consists of a smooth L-shaped rod located in a horizontal plane and a sleeve A of mass m attached by a weight less spring to a point B. The spring stiffness is equal to x. The whole system rotates with a constant angular velocity ω about a vertical axis passing through the point O. Find the elongation of the spring. How is the result affected by the rotation direction?
View SolutionFind total energy of the inclined rod of mass m shown in figure-5.39 , rotating with angular velocity ω , about a vertical axis XX', shown in figure .

View SolutionTwo masses M and m are attached to a vertical axis by weightless threads of combined length l . They are set in rotational motion in a horizontal plane about this axis with constant angular velocity ω . If the tensions in the threads are the same during motion, the distance of M from the axis is
View Solution
