A particle of mass 2kg is moving of a straight line under the actin force F=(8−2x)N. It is released at rest from x=6m.
a. Is the partical moving simple harmonically.
b.Find the equilibrium position of the particle.
c. Write the equation of motion of the partical.
d. Find the time period of SHM.
The correct Answer is:a. Yes
b. x=4m
c.x=4+2cost
d.2πsec
f=8−2x
or F=−2(x−4)
For equilibrium position F=0
⇒x=4 is equilibrium position
Hence the motion of the partuical is SHM with force canstant 2 and equilibrium positionx=4 .
a. Yes, motion is SHM.
b. Equilibrum position is x=4
c. At x=6m. Partical is rest ia at rest , i. e. it is one of the the extreme position.
Hence amplitude A is 2 m and initial partical is at the exterme position.
Therefore, equation of SHM can be written as
x−4=2cosωt,whereω=√km=√22=1
i.e. x=4+cost
d. Time period T=2πω=2πsec.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single Correct107videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct35videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.223videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger11videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type3videos
MISCELLANEOUS KINEMATICS
Similar Questions
A particle of mass 2kg is moving of a straight line under the actin force F=(8−2x)N. It is released at rest from x=6m.
a. Is the particle moving simple hormonically.
b. Find the equilibrium position of the particle.
c. Write the equation of motion of the particle.
d. Find the time period of SHM.View SolutionA particle of mass 2kg is moving of a straight line under the actin force F=(8−2x)N. It is released at rest from x=6m.
a. Is the particle moving simple hormonically.
b. Find the equilibrium position of the particle.
c. Write the equation of motion of the particle.
d. Find the time period of SHM.View Solution
Knowledge Check
- Question 1 - Select One
A particle of mass 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is
A2π5sB2√2π5sC√2π5sD4π5s - Question 2 - Select One
A particle of mass 0.2 kg moves with simple harmonic motion of amplitude 2 cm. If th~ total energy of the particle is 4×10−5 J, then the time period of the motion is
A2π secondsB3π2 secondsCπ secondsDπ2 seconds - Question 3 - Select One
A partical moves in the x−y plane according to the scheme x=−8sinπt and y=−2cos2πt, where t is time. Find the equation of path of the particle
Ay=−2+x216By2=−2+x216Cx2=−2+y216Dx=−2+y216
A particle of mass 2kg is moving on a straight line under the action of force F=(8−2x)N. The particle is released at rest from x=6m. For the subsequnent motion(All the value in the right column are in their S.I. units)
_E01_071_Q01.png)
View SolutionFor a particle performing SHM, equation of motion is given as d2dt2+4x=0. Find the time period
View SolutionA partical executing simple harmonic motion has amplitude of 1m and time period 2sAtt=0, net force on the partical is zero. Find the equation of displacement of the partical.
View SolutionA particle having mass 2 kg is moving along straight line 3x+4y=5 with speed 8m/s . Find angular momentum of the particle about origin, x and y are in meters.
View SolutionA particle of mass = 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is nπ5 second. Find value of n.
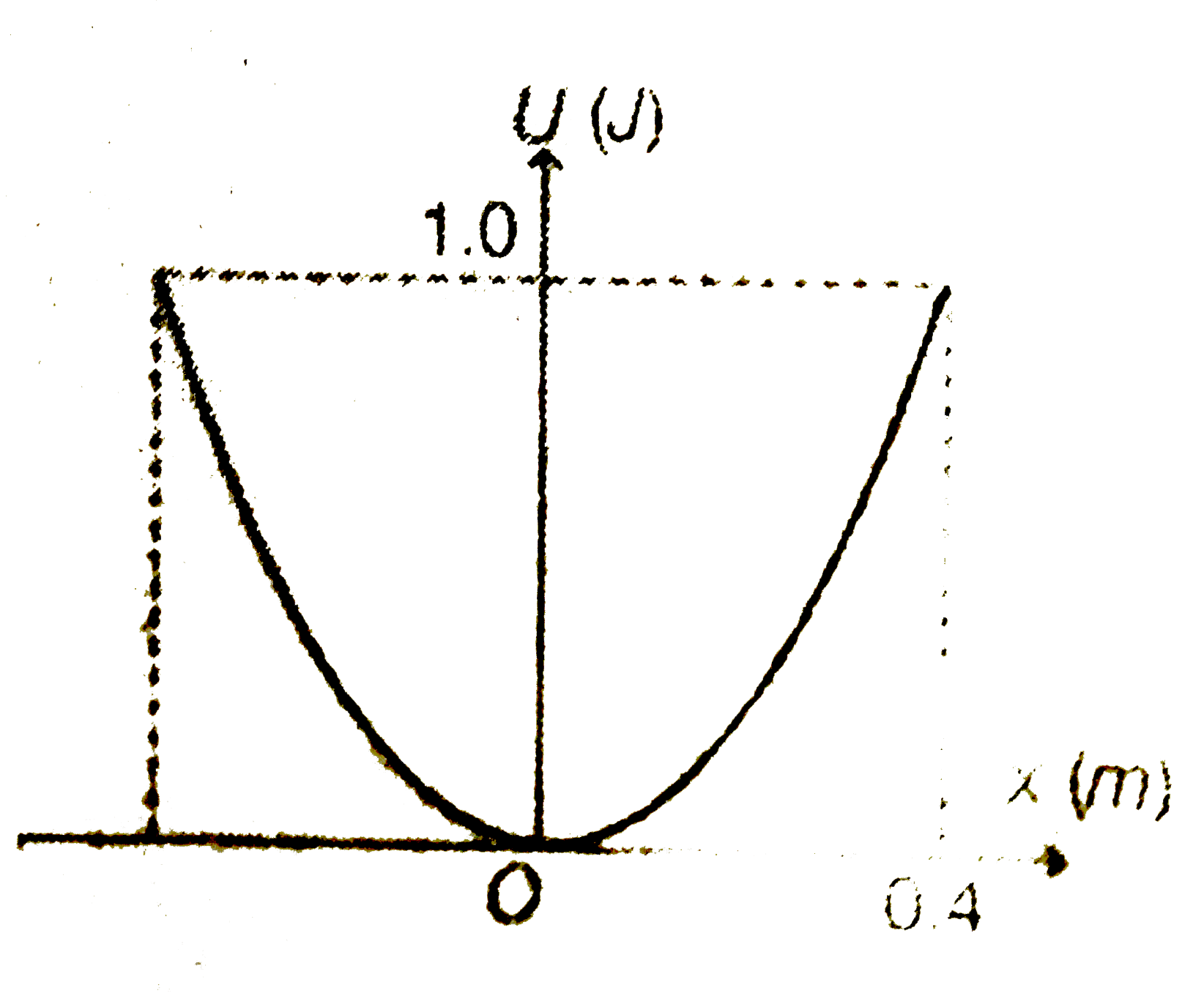View Solution