If velocity of a partical moving along a straight line changes sinusoidally with time as shown in given graph. Find the average speed over time interval t=0 to t=2(2n−1) second, n being any positive interget.
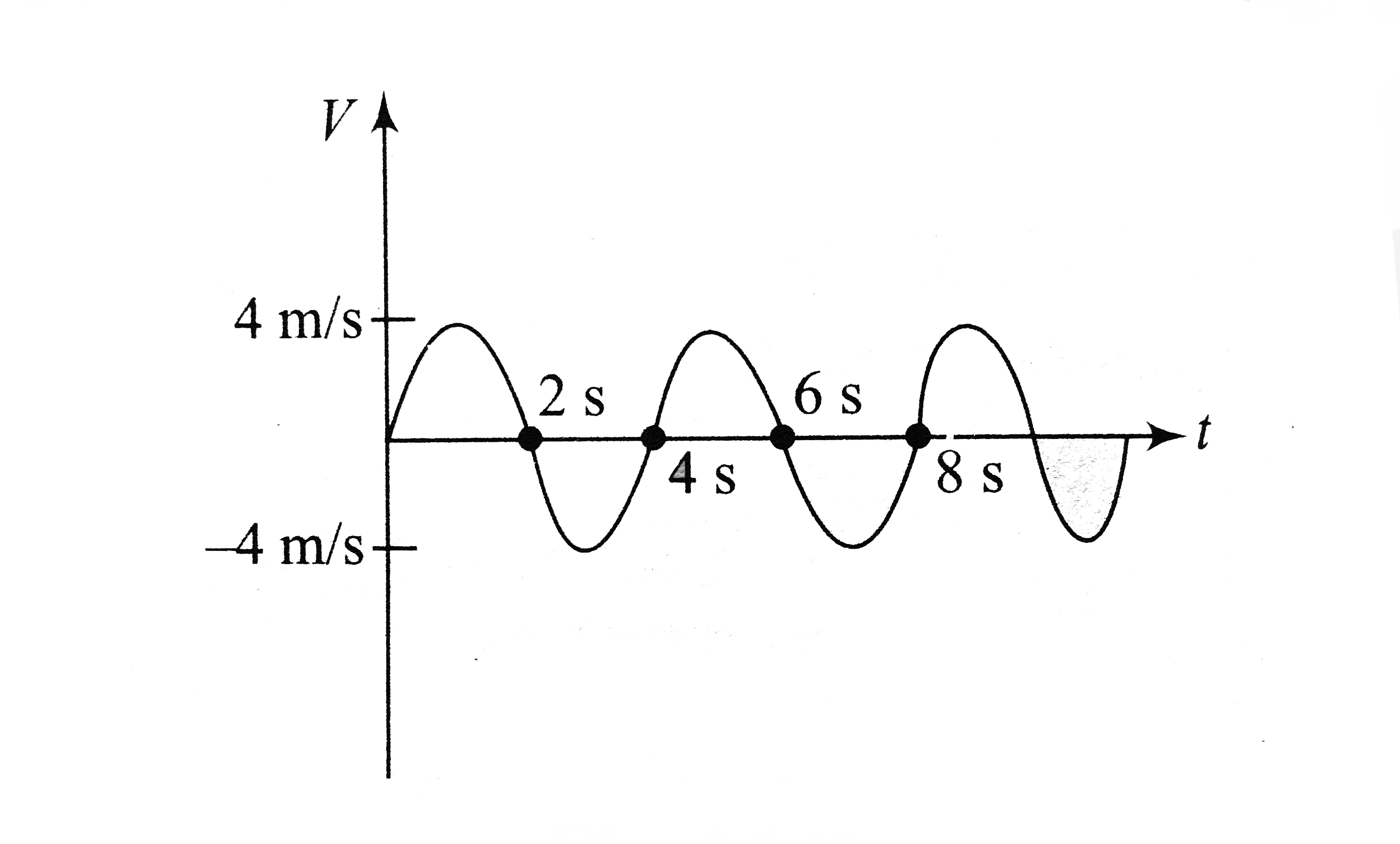
The correct Answer is:8πm/s
Method1 :
Average speed =Total distance travell edTotal time taken=g2(2n−1)
Here Δt=2(2n−1)=4n−=4(n−1)+2
From the graph it is clear that time period Tis4s
∴ΔT=(n−1)T+T2
Total distance travelled in one time period =4A where A is amplitude.
Therefore, total distance travelled in Δt is
S=(n−1)4A+2A=(2n−1)2A
∴>v<=(2n−1)2A2(2n−1)=A and ωA=vmax=4
⇒2π4A=4
⇒A=8π∴>v<8πm/s
Method 2
It can be observed from the graphthat average speed in time interval t=0 to t=2s is same as that in intervals t=0 to t=4s t=0, to t=8s, t=0 to t=12s
or t=0 to t=2(2n−1)s
The speed as function of time is
v=∣∣∣4sin(2π)Tt∣∣∣=∣∣∣4sin(2π)4t∣∣∣=∣4sin(πt)2
v=∣∣∣4sin(2πT)t∣∣∣=∣∣∣4sin(2π4)t∣∣∣=∣∣∣4sin(πt2)∣∣∣
The average speed on time interval t=0 to t=2s is
¯v=∫20vdt∫20dt=(∫204sin πt2dt)2=8πms
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single Correct
107 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.2
23 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
Knowledge Check
The velocity-time plot is shown in figure. Find the average speed in time interval t=0 to t=40s during the period.
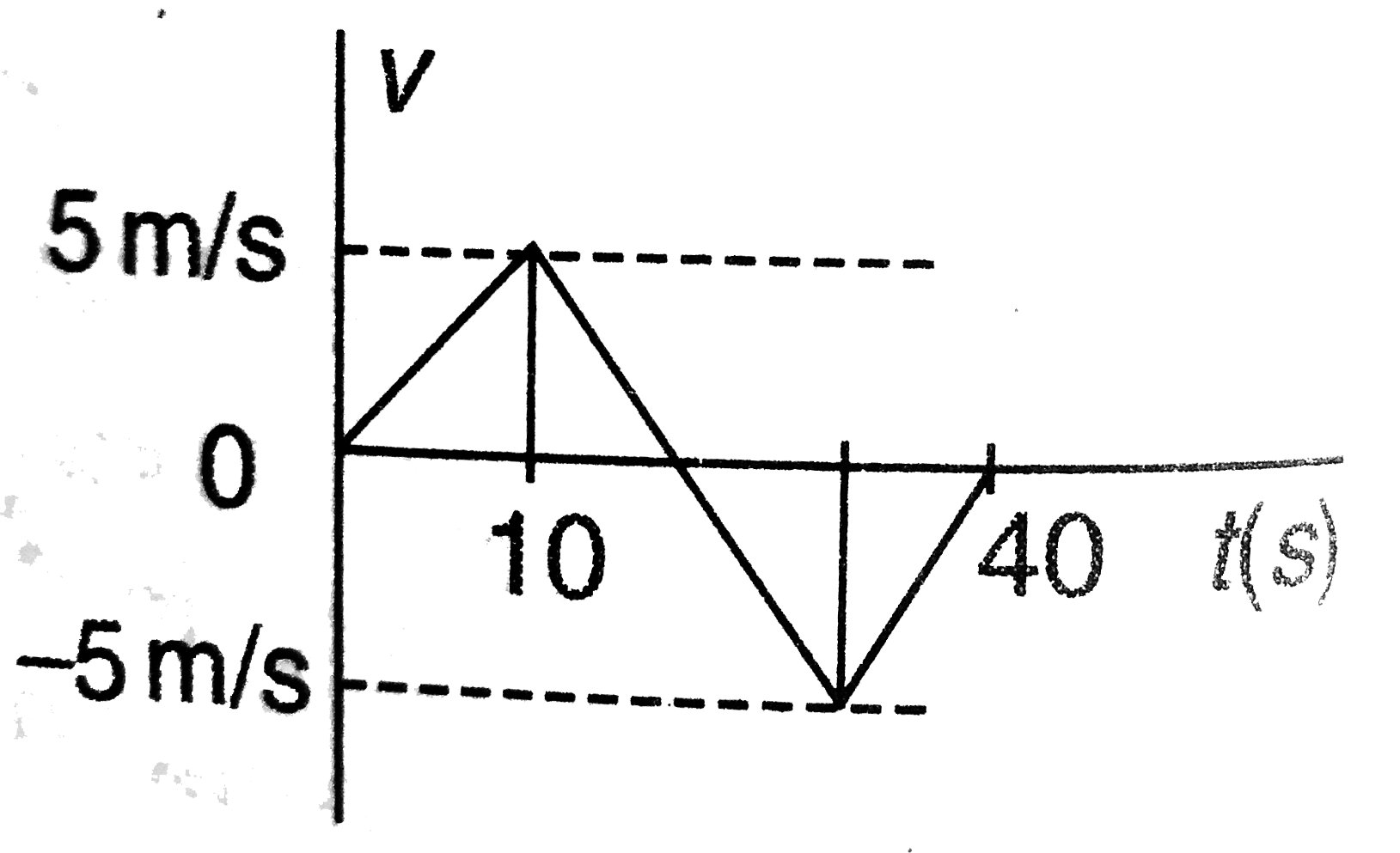 AzeroB2.5m/sC5m/sDnone
AzeroB2.5m/sC5m/sDnoneThe position (x) - time (t) graph for a particle moving along a straight line is shown in figure. The average speed of particle in time interval t = 0 to t = 8 s is
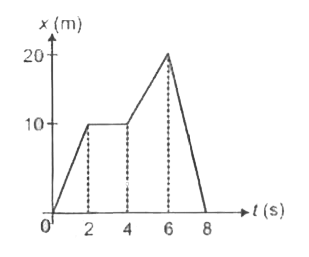 AZeroB5 m/sC7.5 m/sD9.7 m/s
AZeroB5 m/sC7.5 m/sD9.7 m/sPosition time graph is given find average speed in time t=0 and t=15sec is
 A5m/sB53m/sC2m/sD23m/s
A5m/sB53m/sC2m/sD23m/s
The velocity-time graph of a particle moving along a straight line is shown in the figure-given below
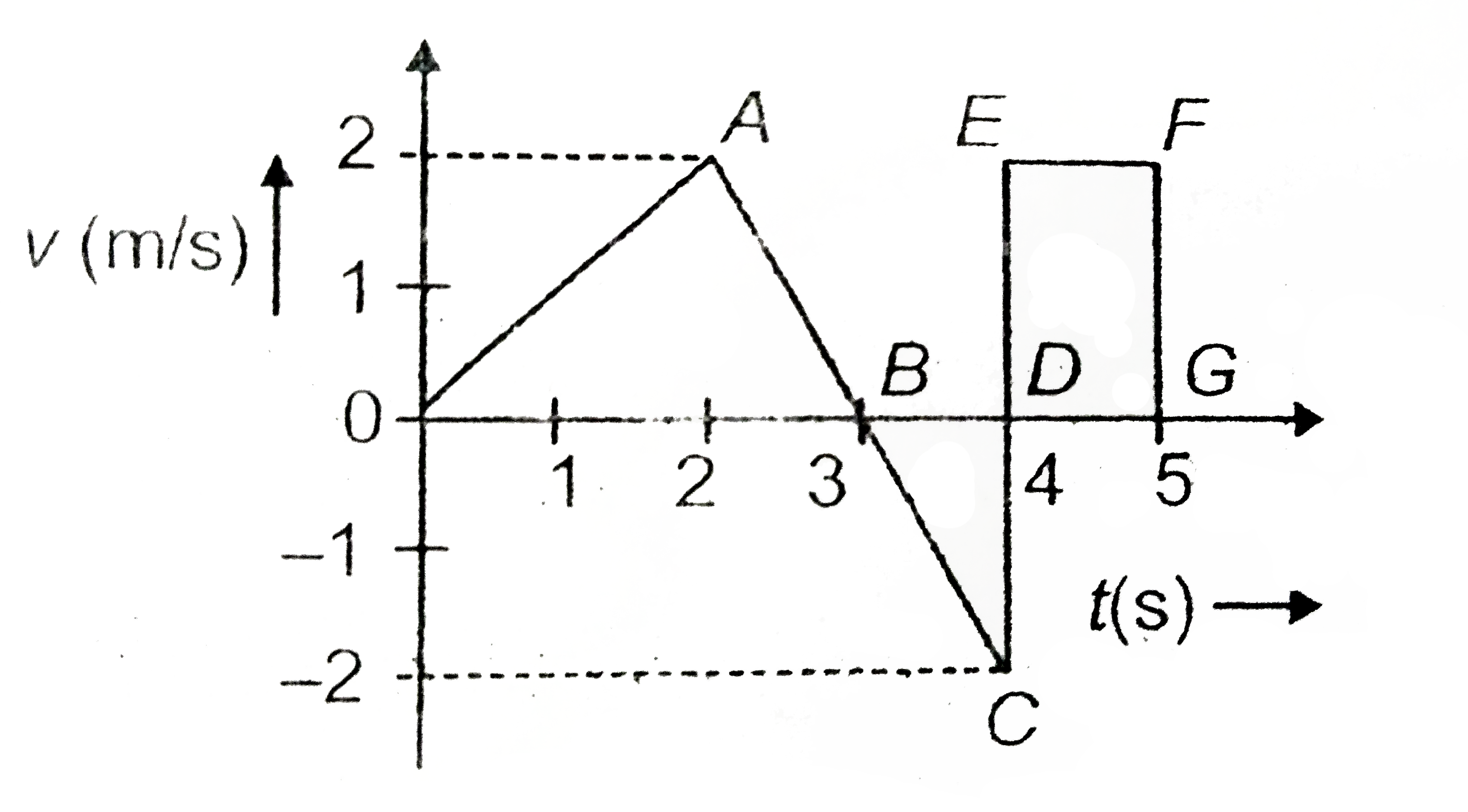
The displacement of the particle in 5 second is
View SolutionThe x-t graph of a particle moving along a straight line is shown in figure

The speed-time graph of the particle is correctly shown by
View SolutionThe velocity - time graph of a particle moving along a straight line is shown in the figure given below
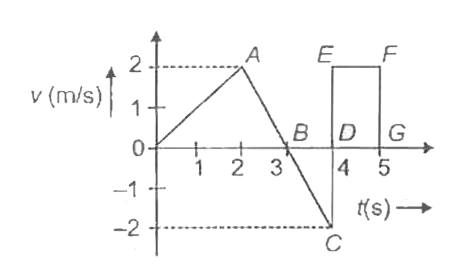
The displacement of the particle in 5 second is
View SolutionThe velocity time graph of a body moving along a straight line is shown in figure. The ratio of the average velocities during the time t1 and t2 is.
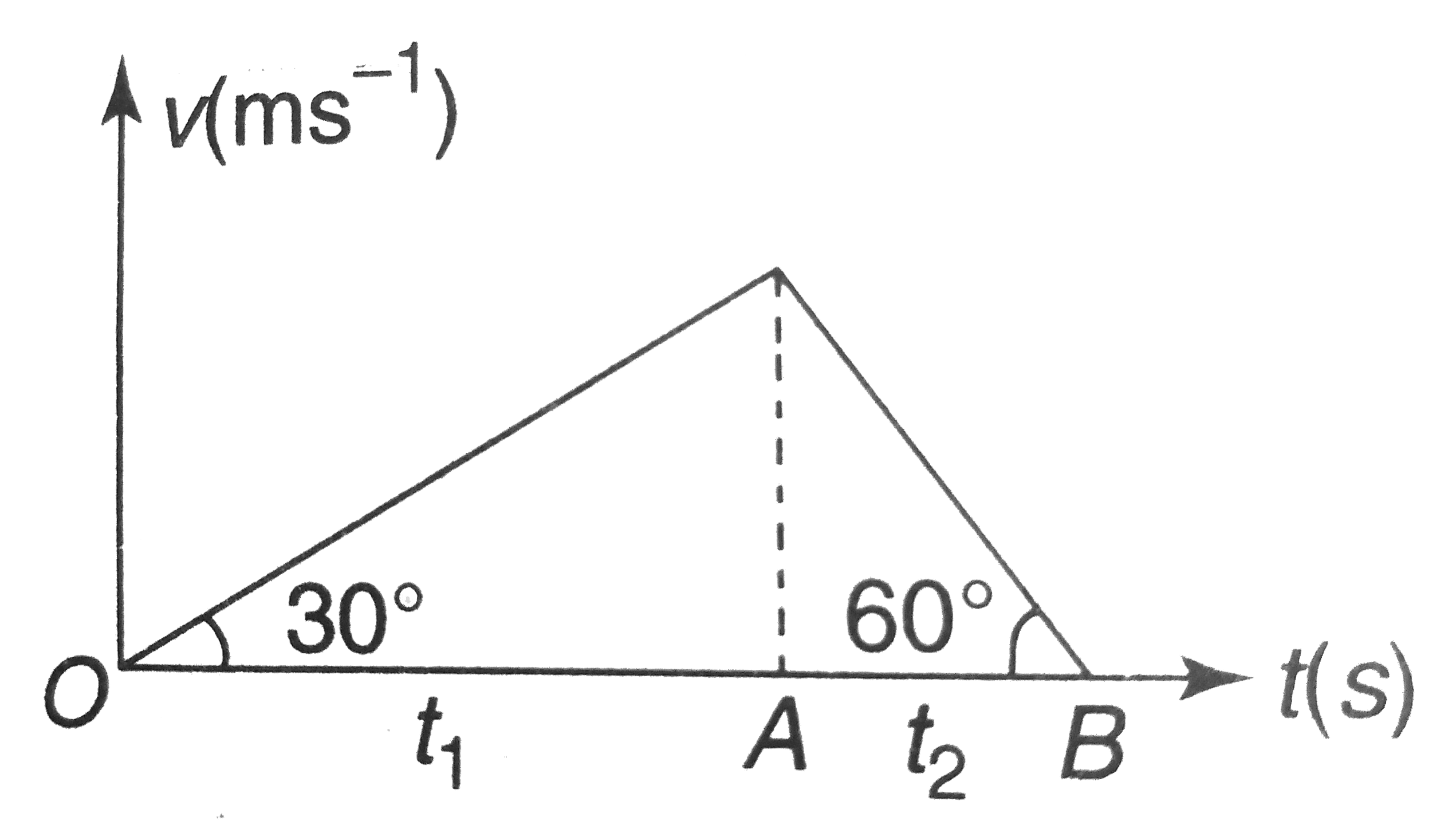
View SolutionA body moves in a straight line along Y-axis. Its distance y in metre) from the origin is given y=8t−3t2. The average speed in the time interval from t=0 second to t=1 second is
View Solution
