In the figure shown in the text, if the block is a cube of side a
find
(a). ω just after impact
(b). Loss of mechanical enegy during impact
(c) minimum value of v so as the block overcomes the obstacle and does not turn back.
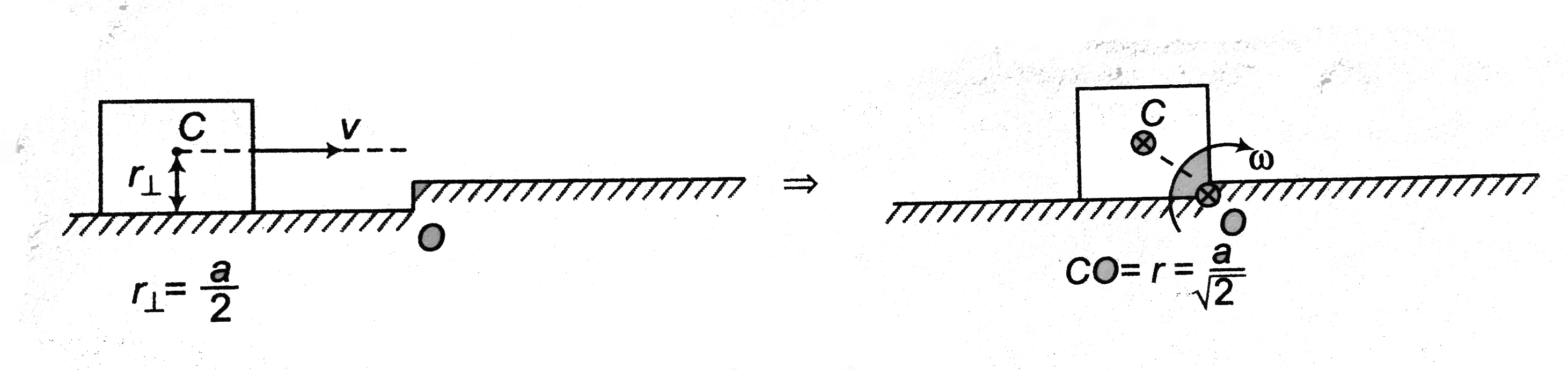
(a). From conservation of angular momentum about O
Li=Lf
mvcr⊥=Ioω=(Ic+mr2)ω
⇒mv(a2)=⎡⎣ma26+m(a√2)2⎤⎦ω
⇒ω=34(va)
(b). loss of mechanical energy
=Ei−Ef
=12mv2−12Ioω2
=12mv2−12⎡⎣ma26+m(a√2)2⎤⎦(34va)2
=516mv2,Brgt (c) 
Block overcomes the obstacle at O if centre of mass rises upto a height a√2 as shown in figure (from the initial height a2)
Because after that torque of mg about O will itself rotate the block on other side as shown in figure
∴ decrease in rotational kinetic energy = increase in gravitational potential energy
∴12Ioω2=mg(1√2−a2)
or 12⎡⎣ma26+m(a√2)2⎤⎦[34va]2=mg (a√2−a2)
∴v=√1.1ga

Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Miscellaneous Examples
2 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Solved Example
1 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
In the situation discussed above, find
(a) velocity of combined mass just after collision at the bottommost point (oru).
(b) loss of mechanical energy during collision.
(c) minimum value of v0 so that the combined mass completes the vertical circular motion.
View SolutionA block is rotating in contact with vertical wall (rotor) as shown. Find the minimum value of ω so that the block does not slide down.

View Solution
Knowledge Check
In the shown figure, the mass in sticks to the string just after it strikes it. Then the minimum value of h, so that the lower mass bounce off the ground during 'its rebound is:
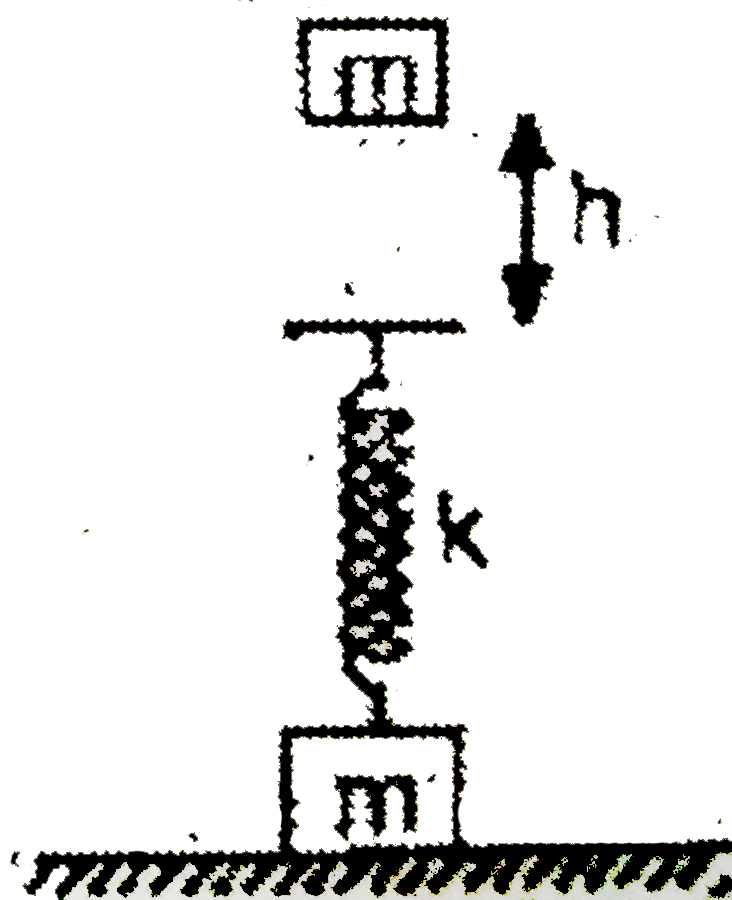 A2mgkB3mgkC3mg2kD6mgk
A2mgkB3mgkC3mg2kD6mgk

Consider the figure shown here of a moving cart C. if the coefficient of friction between the block A and the cart is μ, then calculate the minimum acceleration a of the cart C so that the block A does not fall.
View SolutionA block has a L shaped stand fixed to it. Mass of the block with the stand is M. At the free end of the stand there is a spring which carries a ball of mass m. With the spring in its natural length, the ball is released. It begins to oscillate and the stand is tall enough so that the ball does not hit the block.
(a) Find maximum value of mass (m) of the ball for which the block will not lose contact with the ground?
(b) If the stand is not tall enough and the ball makes elastic impact with the block, will your answer to part (a) change?

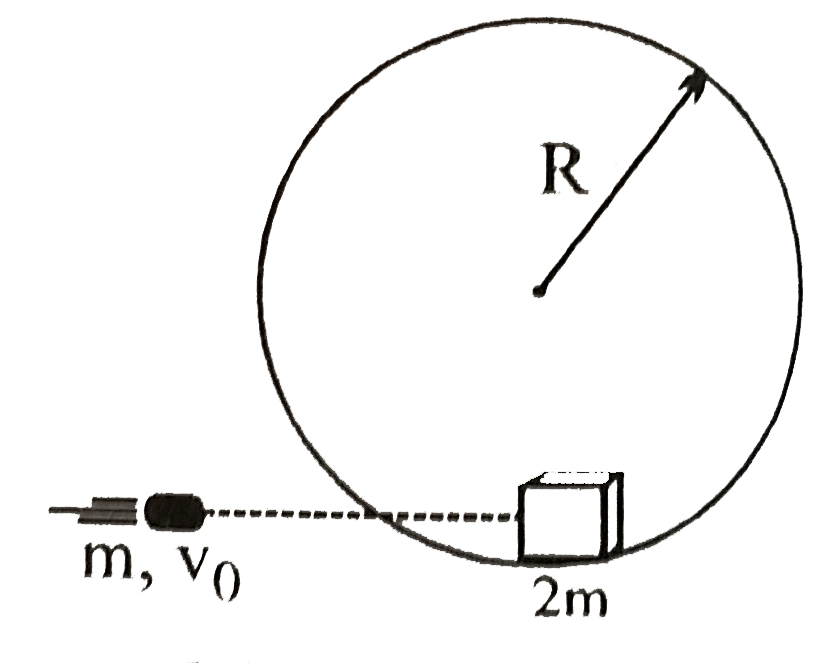
View SolutionA small block of mass 2m initially rests at the bottom of a fixed circular, vertical track, which has a radius of R. The contact surface between the mass and the loop is frictionless. A bullet of mass m strikes the block horizontally with initial speed v0 and remain embedded in the block as the block and the bullect circle the loop. Determine each of the following in terms of m,R and g.
(a) The speed of the masses immediately after the impact.
(b) The minimum initial speed of the bullet if the block and the bullet are to successfully execute a complete ride on the loop
View SolutionA small block is placed on the top of a smooth inverted hemispherical bowl of radius R.

(a) The bowl is given a sudden impulse so that it begins moving horizontally with speed V. Find minimum value of V so that the block immediately loses contact with the bowl as it begins to move. (b) The bowl is given a constant acceleration ‘a’ in horizontal direction. Find maximum value of ‘a’ so that the block does not lose contact with the bowl by the time it rotates through an angle θ=1∘ relative to the bowl. You can make suitable mathematical approximations justified for small value of angle θ.
View SolutionA solid cube of side 'a' is shown in the figure. Find maximum value of 100ba for which the block does not topple before sliding.

View SolutionA small block of mass m is projected on a larger block of mass 10m and length l with a velocity v as shown in the figure. The coefficient of friction between the two block is μ2 while that between the lower block and the ground is μ1. Given that μ2>11μ1.

(a) Find the minimum value of v, such that the mass m falls off the block of mass 10m .
(b) If v has minimum value, find the time taken by block m to do so.
View SolutionA block of mass m is dropped onto a spring of constant k from a height h. The second end of the spring is attached to a second block of mass M as shown in figure. Find the minimum value of h so that the block M bounces off the ground. If the block of mass m sticks to the spring immediately after it comes into contact with it.

View Solution
