In the figure shown masses of the blocks A, B and C are 6kg, 2kg and 1kg respectively. Mass of the spring is negligibly small and its stiffness is 1000 N//m. The coefficient of friction between the block A snd the table is μ=0.8. Initially block C is held such that spring is in relaxed position. The block is released from rest. Find (g=10m/s2).

(a) the maximum distance moved by the kinetic C.
the acceleration of each block, when clongation in the spring is maximum.
The correct Answer is:A, B, C
μmAg=0.8×6×10=48N
(mB+mC)g=(1+2)×10=30N
Since (mB−mC)g>μmAg,aA=aB=0.
From conservation of energy principal we can prove that maximum distance moved by C or maximum extension in the spring would be
xm=2mCgk=2×1×101000
=0.02m
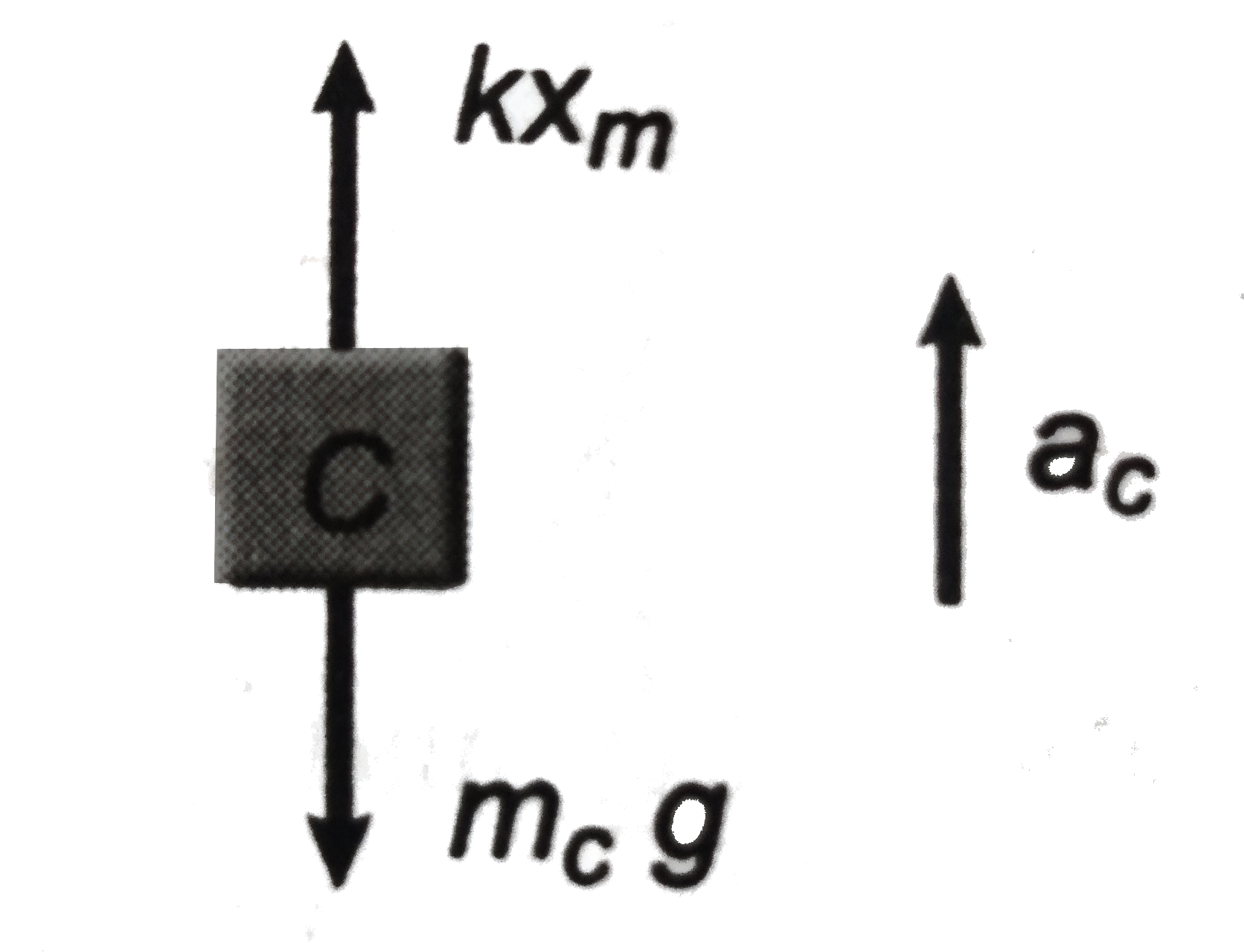
At maximum extension
aC=kxm−mCgmC
Substituting the values we have,
aC=10m/s2.
Topper's Solved these Questions
- WORK, ENERGY & POWERBook:DC PANDEYChapter:WORK, ENERGY & POWERExercise:Level 2 Comprehension Based
Explore 2 Videos
- WORK, ENERGY & POWERBook:DC PANDEYChapter:WORK, ENERGY & POWERExercise:Level 2 More Than One Correct
Explore 9 Videos
- WAVE MOTIONBook:DC PANDEYChapter:WAVE MOTIONExercise:Integer Type Question
Explore 11 Videos
- WORK, ENERGY AND POWERBook:DC PANDEYChapter:WORK, ENERGY AND POWERExercise:MEDICAL ENTRACES GALLERY
Explore 33 Videos
Similar Questions
The figure shows the variation of potential energy of a particle as a funcation pf x, the x-coordination of the region. It has been assumed that potential energy depends only on x. For all other values x,U is zero. i.e. forx<−10 and x>15,U=0.
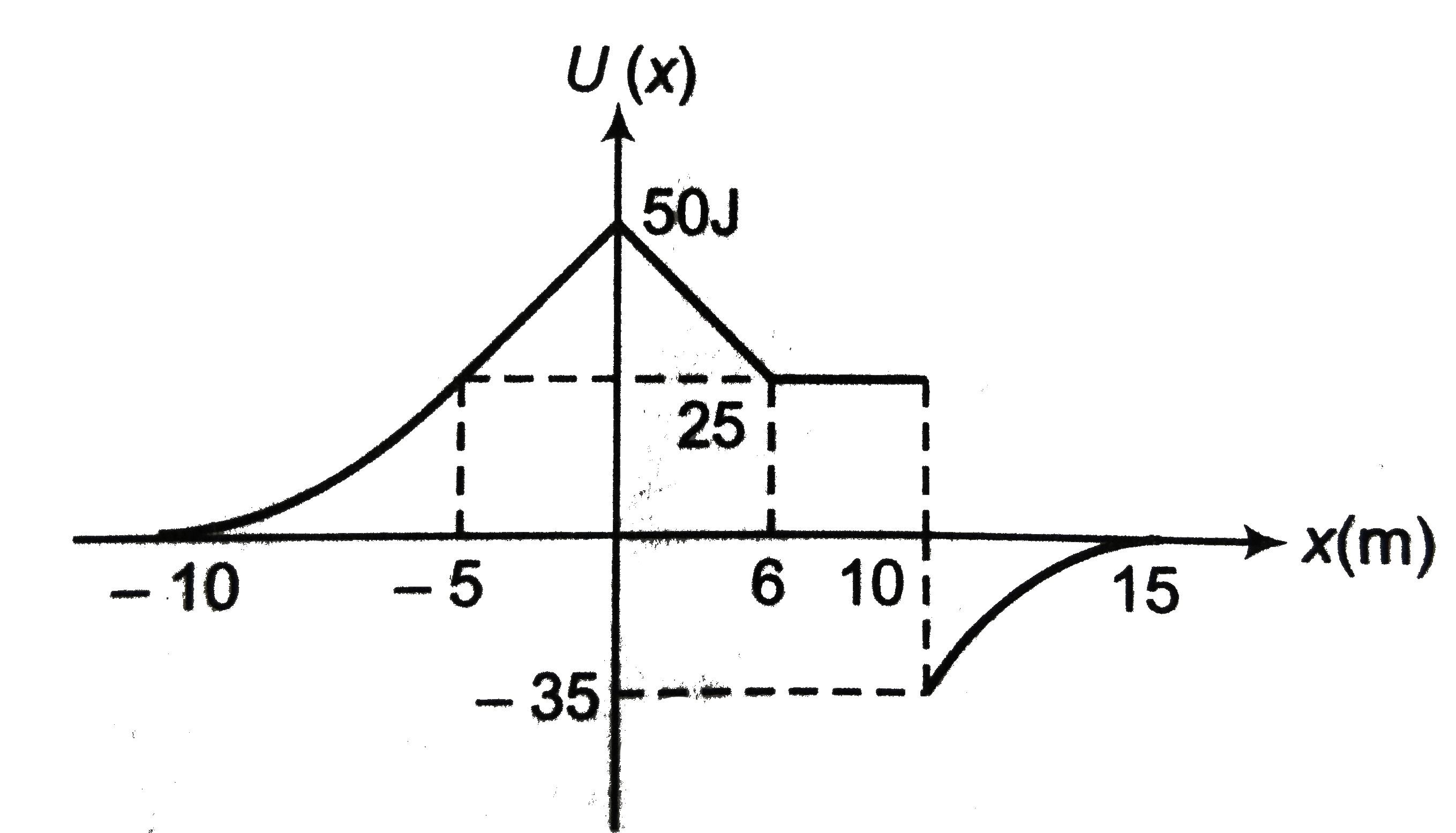
If total mechanical energy of the particle is 25J, then it can found in the region
View SolutionThe potential energy of a particle of mass 5 kg moving in xy-plane is given as U=(7x+24y) joule, x and y being in metre. Initially at t=0, the particle is at the origin (0,0) moving with velovity of (8.6ˆi+23.2ˆj)ms1, Then
View SolutionTwo wires of same material of radii 2r and r are welded together end to end The combination is used as a sonometer wire and is kept under tension T. The welded point lies midway between the bridges. What wil be the ratio of the number of loops formed in the wires, such that the joint is node when the stationary waves are set up in the wire?
View SolutionA body of mass 1kg begins to move under the action of a time dependent force →F=(2tˆI+3t2ˆj)N, where ˆi and ˆj are unit vectors along x-and y-axes. What power will be developed by the force at the time t ?
View SolutionA block of mass m is connected with a rigid wall by light spring of stiffness k. Initially the spring is relaxed.

If the block is pushed with a velocity v0, it oscillates back and forth and stops. Assuming μ as the coefficient of kinetic friction between block and ground, find the work done by friction till the block stops.
View SolutionIn figure, the stiffness of the spring is k and mass of the block is m . The pulley is fixed. Initially, the block m is held such that the elongation in the spring is zero and then released from rest. Find: a. the maximum elongation in the spring. b. the maximum speed of the block m . Neglect the mass of the spring and that of the string. Also neglect the friction.
View SolutionA block of mass m is released from rest onto a spring. A having stiffness kA=mg/2h as shown in figure. If the block compresses spring B through a distance h, find the:
a. stiffness of the spring B
b. equilibrium position of the block
c. maximum velocity of the block
d. maximum acceleration of the block
View SolutionA block with mass 0.50 kg is forced against a horizontal spring of negligible mass , compressing the spring a distance of 0.20 m (figure). When released, the block moves on a horizontal table top for 1.00N//m . What is the coefficient of kinetic friction mu _(k) , between the block and the block and the table?
View SolutionThe coefficient of friction between the block A of mass m & block B of mass 2m is mu . There is no friction between A & B is released from rest & there is no slipping between A & B then:
View SolutionThe coefficient of friction between the block A of mass m & block B of mass 2m is μ. There is no friction between block B & the inclined plane. If the system of blocks A & B is released from rest & there is no slipping between A & B then :
View SolutionConsider the system shown in the figure. Coefficient of friction between the block and table is μ=0.5. The system is released from rest. Find the work done by friction, when the speed of block is 10 m/s (m=1kg)
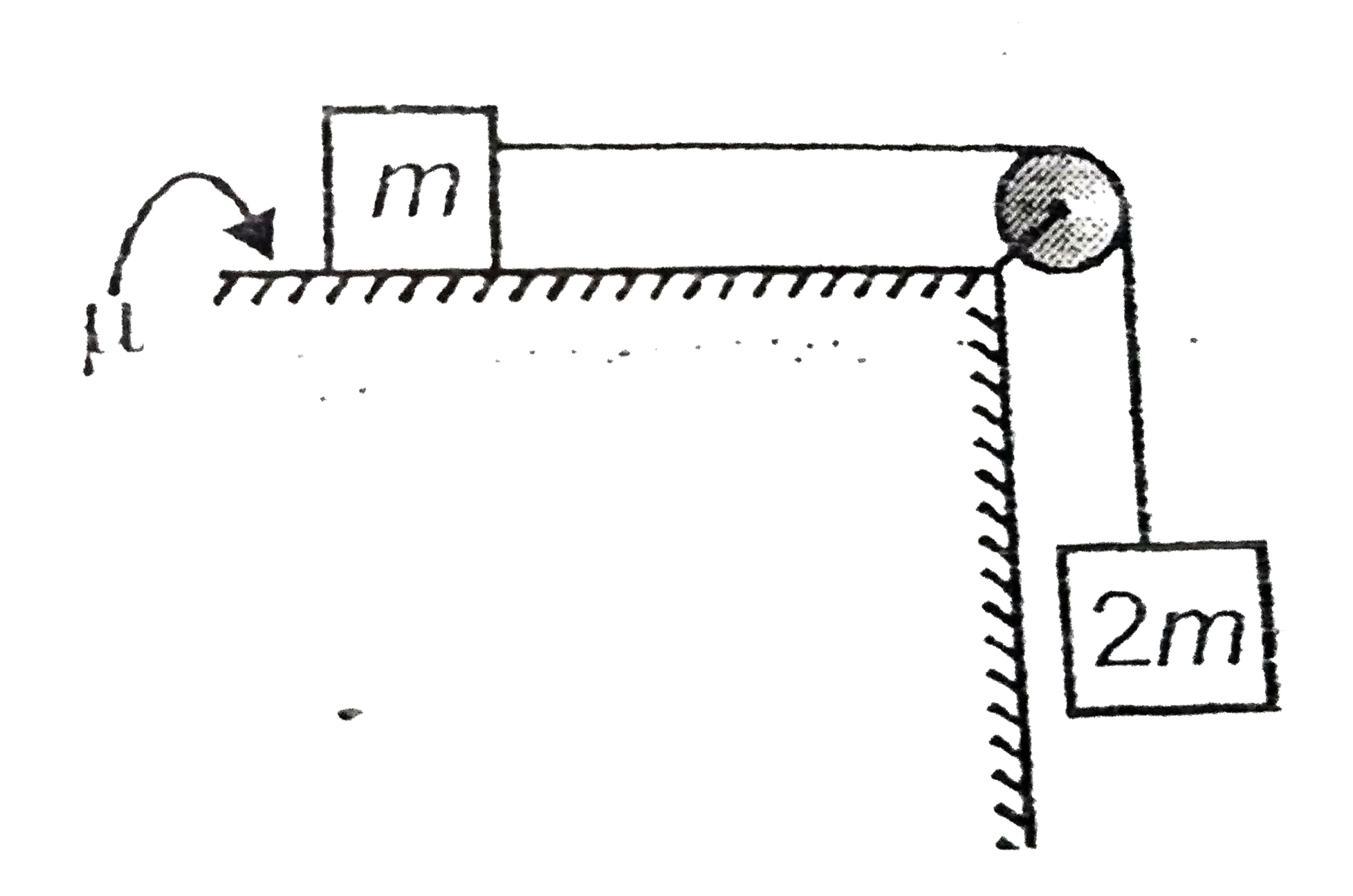
View SolutionA spring is connected between two blocks as shown in the diagram. Initially the blocks are held stationary and suddenly they are released. Find the ratio of maximum kinetic energy with spring compressed the block of mass m to that of mass 2m.
View SolutionA block of mass m attached with a an ideal spring of force constant k is placed on a rough inclined plane having inclination theta with the horizontal and coefficient of friction mu=1//2 tan theta , Initially the block is held stationary with the spring in its relaxed state, find the maximum extension in the spring if the block is released.
View SolutionA 2kg block is connected with two springs of force constants K1=100 N/m and K2=300 N/m as shown in figure. The block is released from rest with the springs unstretched. Find the acceleration of the block in its lowest position (g=10m/s2)

View SolutionA 2kg block is connected with two springs of force constants K_(1) = 100 N/m and K_(2) = 300 N/m as show in figure. The block is released from rest with the springs unstreched. Find the acceleration of the block in its lowest position (g = 10 m//s^(2))
View Solution