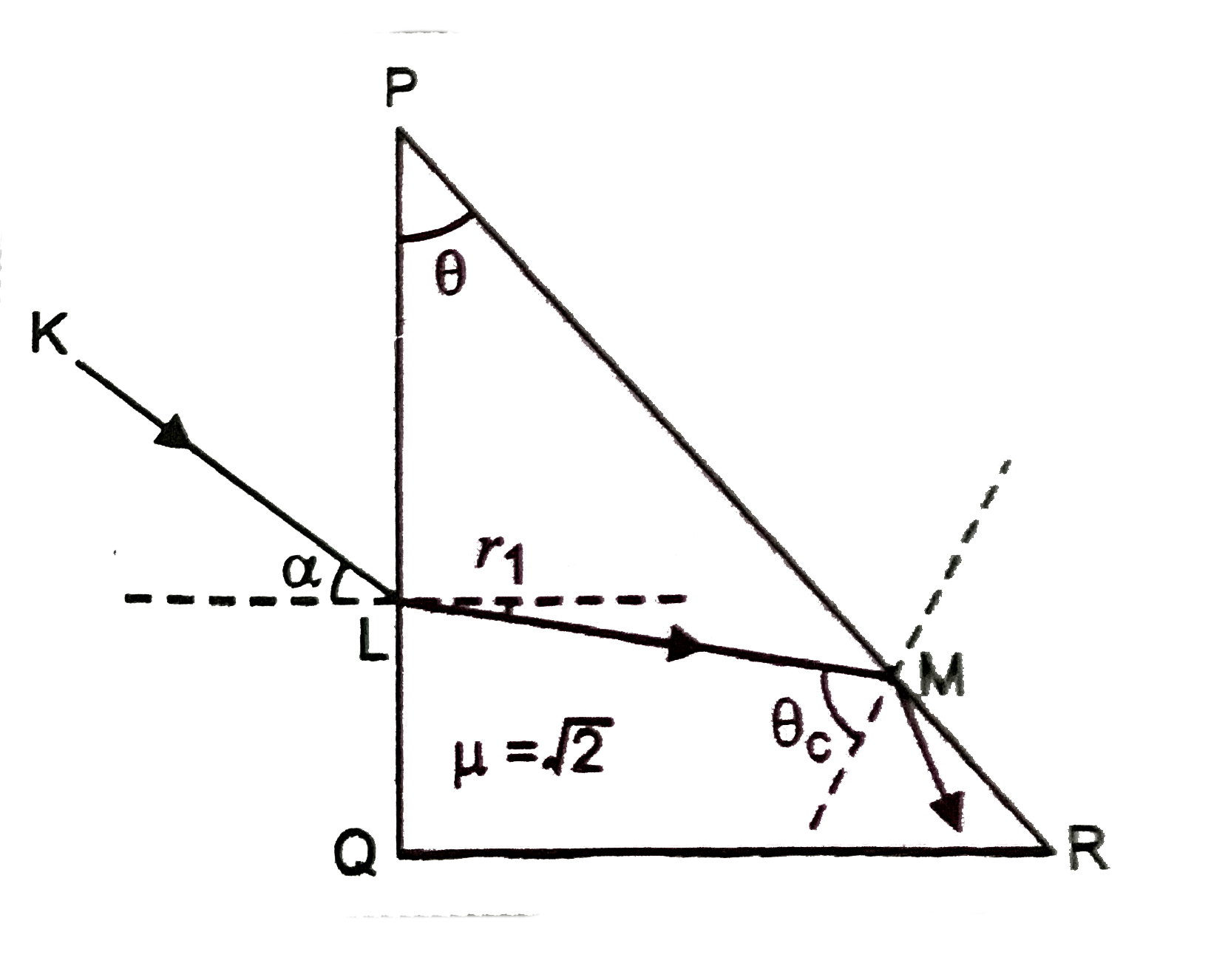
Light is incident at an angle α on one planar end of a transparent cylindrical rod of refractive index μ. Determine the least value of μ so that the light entering the rod does not emerge from the curved surface of rod irrespective of the value of α
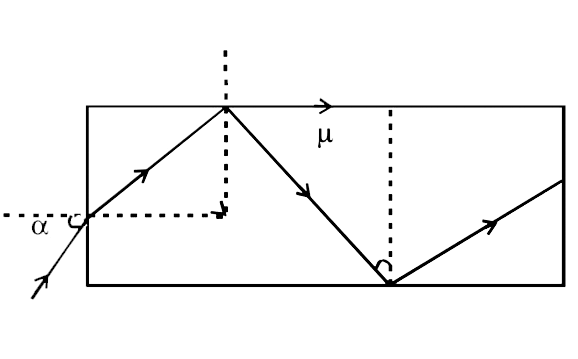
The correct Answer is:C
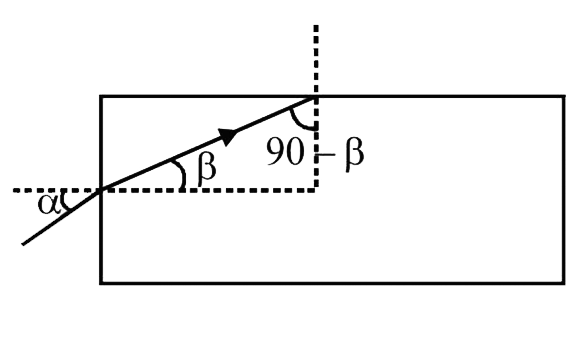
The light entering the rod does not emerge from the curved surface of the rod when the angle (90∘−β) is greater than the critical angle.
i.e., μ≤1sinC Where C is the critical angle.
Here, C=90−β
⇒μ≤1sin(90∘−β)⇒μ≤1cosβ
As a limiting case,μ=1cosβ ....(i)
Applying Snell's law at A
μ=sinαsinβ⇒sinβ=sinαμ ....(ii)
NOTE: The smallest angle of incidence on the curved surface is when α=π2.Thiscanbetakenasalimit∈gcasefor∠of∈cnceonpla≠surface.From(ii)<br>sinbeta=(sinpi/(2))/(mu)impliesmu=(1)/(sinbeta)...(iii)<br>From(i)and(ii),sinbeta=cosbetaimpliesbeta=45^circ<br>impliesμ=1cos45∘=11√2⇒μ=√2
This is the least value of the refractive index of rod for light entering the rod and not leaving it from the curved surface.
Topper's Solved these Questions
Similar Questions
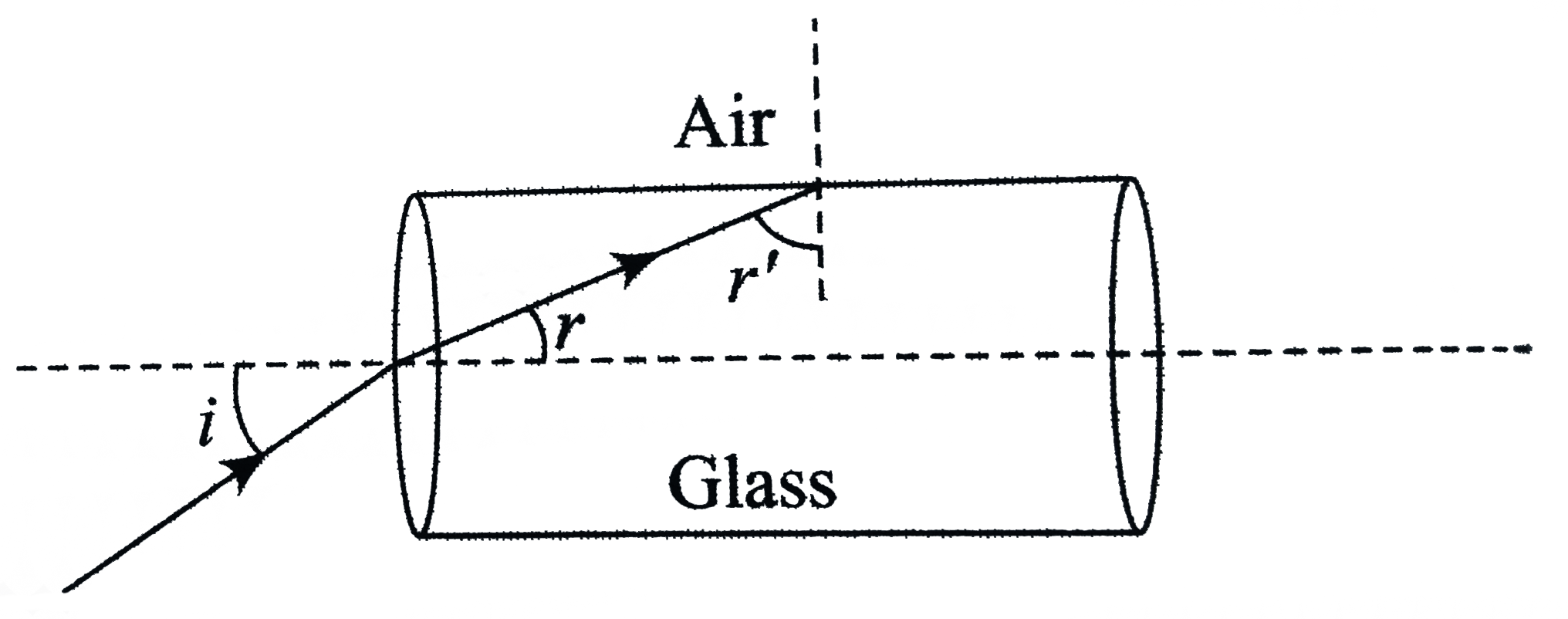
Light is incident at an angle i on one planer end of a transparent cylinderical rod of refractive index μ. Find the least value of μ so that the light entering the rod does not emerge from the curved surface of the rod irrespective of the value of i.

View SolutionWhat should be the value of refractive index n of a glass rod placed in air, so that the light entering through the flat surface of the rod does not cross the curved surface of the rod?
View Solution
Knowledge Check
Light enters at an angle of incidence in a transparent rod of refractive index n. For what value of the refractive index of the material of the rod the light once entered into it will not leave it through its lateral face whatsoever be the value of angle of incidence.
An gt√2Bn = 1Cn = 1.1Dn = 1.3Light enters at an angle of incidence in a transparent rod of refractive index n. For what value of the refractive index of the material of the rod the light once entered into it will not leave it through its lateral face whatsoever be the value of angle of incidence.
An>√2Bn=1Cn=1.1Dn=1.3Light enters at an angle of incidance in a tranjsparent road of refractve index μ. for what value of the refractive index of the material of the rod the light once entered into it will not leave it through its lateral face whatsoever be the value of angle of incidance ?
Aμ>√2Bμ=1Cμ=1.1Dμ=1.3
Monochromatic light falls at an angle of incidence i on a slab of a transparent material (refractive index μ). If reflected and refracted rays are mutually perpendicular, find the relation between μ and i.
View SolutionA ray of light is incident at an angle of 60∘ on one face of a prism which has refracting angle of 30∘ . The ray emerging out of the prism makes an angle of 30∘ with the incident ray. If the refractive index of the material of the prism is μ=√a , find the value of a .
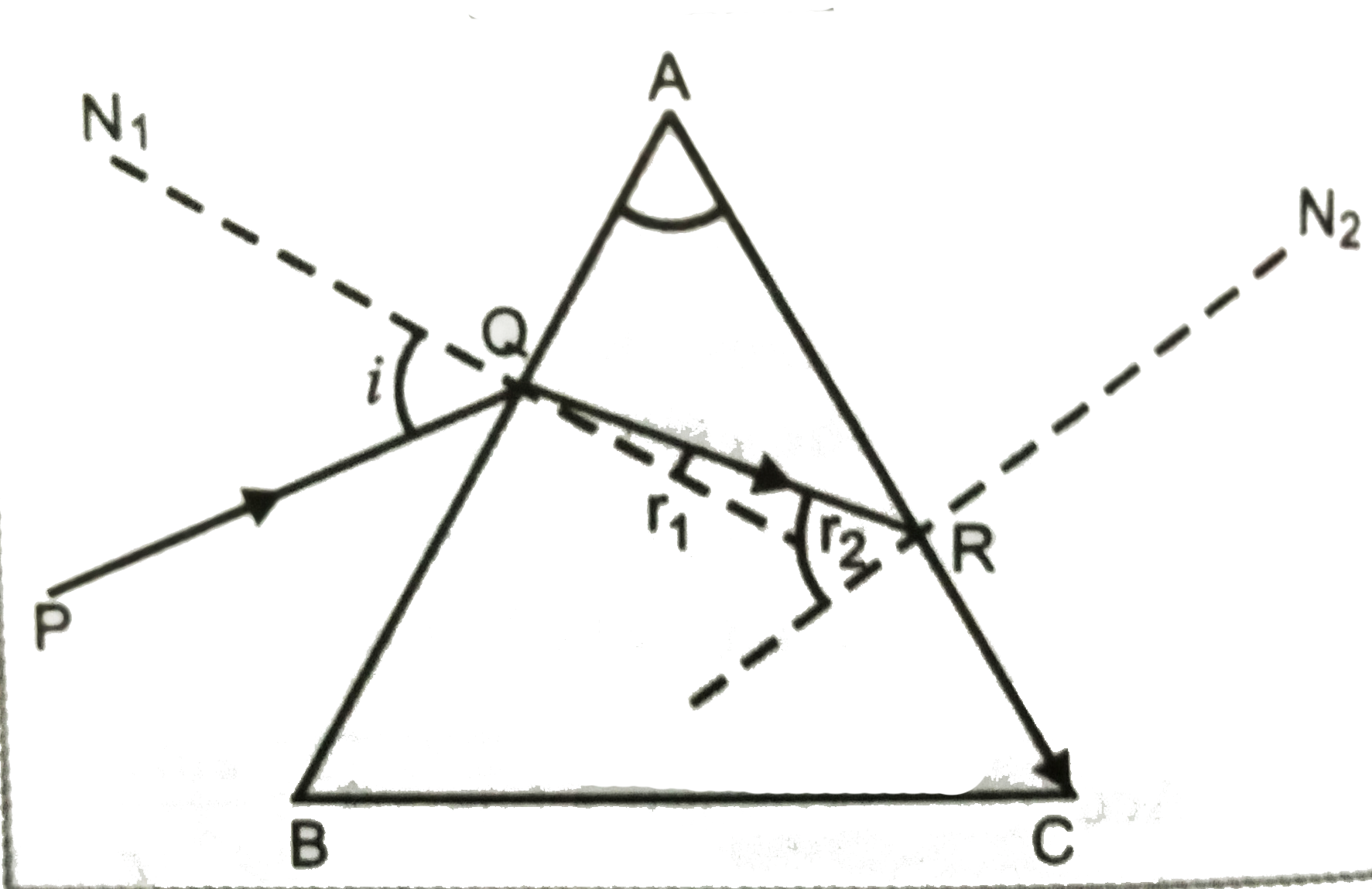
View SolutionA ray of light enters the face AB of a glass prism of refractive index μ at an angle of incidence i. Find the value of i such that no ray emerges from the face AC of the prism, given angle of prism is A.
View SolutionA ray of light the face AB of a glass prism of refractive index μ at an angle of incidence i. Find the value of i such that no ray emerges from the face AC of the prism. Given angle of prism is A.
View SolutionA parallel beam of light is incident from air at an angle α on the side of right angled triangular prism of refractive index μ=√2. Light undergoes total internal reflection in the prism at the face PR when α has a minimum value of 45∘. The angle θ of the prism is.
 .
.
View Solution
