Light of wavelength λ from a small 0.5 mW He-Ne laser source, used in the school laboratory, shines from a spacecraft of mass 1000 kg. Estimate the time needed for the spacecraft to reach a velocity of 1.0km−1 from rest. The momentum p of a photon of wavelength λ is given by p=hλ, where h is Planck's constant.
6..1018
3×1017
6×1017
2×1015
The correct Answer is:C
Photons have momentum (P=hλ) which they carry away, the spacecraft will acquire momentum in the opposite direction according to law of conservation of momentum.
No. of photons per second from laser =n
Then, from energy consideration.
0.5×10−3=nh(cλ)
n=(0.5×10−3)λ(ch)
Rate of change of momentum of spacecraft
np=nhλ=(0.5×10−3)λch(hλ)=0.5×10−3c
From Newton's second law, nhλ=ma
1000a=0.5×10−33.00×108=16×10−11
v=at
t=va=100011000×16×10−11s=6×1017s
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Multiple Correct10videos
PHOTOELECTRIC EFFECT
- BOOK - CENGAGE PHYSICSCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Linked Comprehension44videos
PHOTOELECTRIC EFFECT
- BOOK - CENGAGE PHYSICSCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Subjective16videos
PHOTOELECTRIC EFFECT
- BOOK - CENGAGE PHYSICSCHAPTER - NUCLEIEXERCISE - QUESTION BANK59videos
NUCLEI
- BOOK - CENGAGE PHYSICSCHAPTER - RAY OPTICSEXERCISE - DPP 1.612videos
RAY OPTICS
Similar Questions
Light of wavelength λ from a small 0.5mW He-Ne laser source is used in the school laboratory to shine on perfectly absorbing surface of a spacecraft of mass 1000kg. The tịne needed' for the spacecraft to reachi a velocity of 1kms from rest is given by α×10β(s) in scientific notation. Find the value of (β−r2α).
View Solution_E01_106_Q01.png)
Two parallel beams of light P and Q (separation d) containing radiations of wavelengts 4000Å and 5000 Å (which are mutually coherent in each wavelength separately) are incident normally on a prism as shown in figure the refractive index of the prism as a function of wavelength is given by the relation μ(λ)=1.20+bλ2 where λ is in Å and b is a positive constant. The value of b is such that the condition for total reflection at the face AC is just satisfied for one wavelength and is not satisfied for the other. A convergent lens is used to bring these transmitted beams into focus. If the intensities of the upper and the lower beams immediately after transmission from the face AC, are 4I and I respectively, find the resultant intensity at the focus.View Solution
Knowledge Check
- Question 1 - Select One
The energy of a photon of frequency v is E = hv and the momentum of a photon of wavelength λ is p = hλ From this statement one may conclude that the wave velocity of light is equal to :
A3×108ms−1BEPCEpD(EP)2 - Question 2 - Select One
In a Lloyds's mirror experiment as narraow slit S iransmitting a light of wavelength λ is placed 3 mm above a small plane mirror ( as shown). The light coming directly from the the slit and that coming after the reflection interfere on a screen placed at a distance of 90 cm from the slit. Length of mirror is 2 mm and the middle point of mirror is 2 mm from point P.
If fringe width is 0.1 mm then what is the wavelength of light used ?A3.33×10−7mB6.67×10−7mC1.0×10−7mD4×10s - Question 3 - Select One
A laser light of wavelength 660 nm is used to weld Retina detachment. If a laser pulse of width 60 ms and power 0.5 kW is used, the approximate number of photons in the pulse are (Take Planck's Constant, h=6.62×10−34Js)
A1022B1019C1020D1018
There are two very small natural particle which are held fixed at a separation of 1 m from each other . Using some mechanism , one electron is transferred from particle to the other and electric potential energy lost in this process is converted into a photon of wavelength λ1. When one more electron is transferred in the same direction , the wavelength of photon emitted is λ2 . If λ1−λ2=5p×23q calculate the value of pq.
0123456789View SolutionTwo parallel beams of light P and Q (separation d) containing radiation of wavelengths 4000A and 5000A (which are mutually coherent in each wavelength separately) are incident normally on a prism as shown in fig. The refractive index of the prism as a function of wavelength is given by the relation. μ(λ)=1.20+bλ2 Where λ is in A and b is positive constant. The value of b is such that the condition wave length and is not satisfied for the other.
(a) Find the value of b.
(b) find the deviation of the beams transmitted through the face AC. (c) A convergent lens is used to bring these transmitted beams into focus. If the intensities of transmission form the face AC, are 41 and I respectively, find the resultant intensity at the focus.
View SolutionWhat is the actual wavelength of light (in μm ) emitted by the fixed star towards which the earth is moving with a velocity of 30Kms−1? Given an observer on the earth observes a shift of 0.58Å in the wavelength of light coming from the star.
View SolutionTwo coherent narrow slits emitting sound of wavelength lamda in the same phase are placed parallel to each other at a small separation of 2λ. The sound is detected by moving a detector on the screen ∑ at a distance D(gtgtlamda) from the slit S1 as shown in figure. Find the distance x such that the intensity at P is equal to the intensity at O.
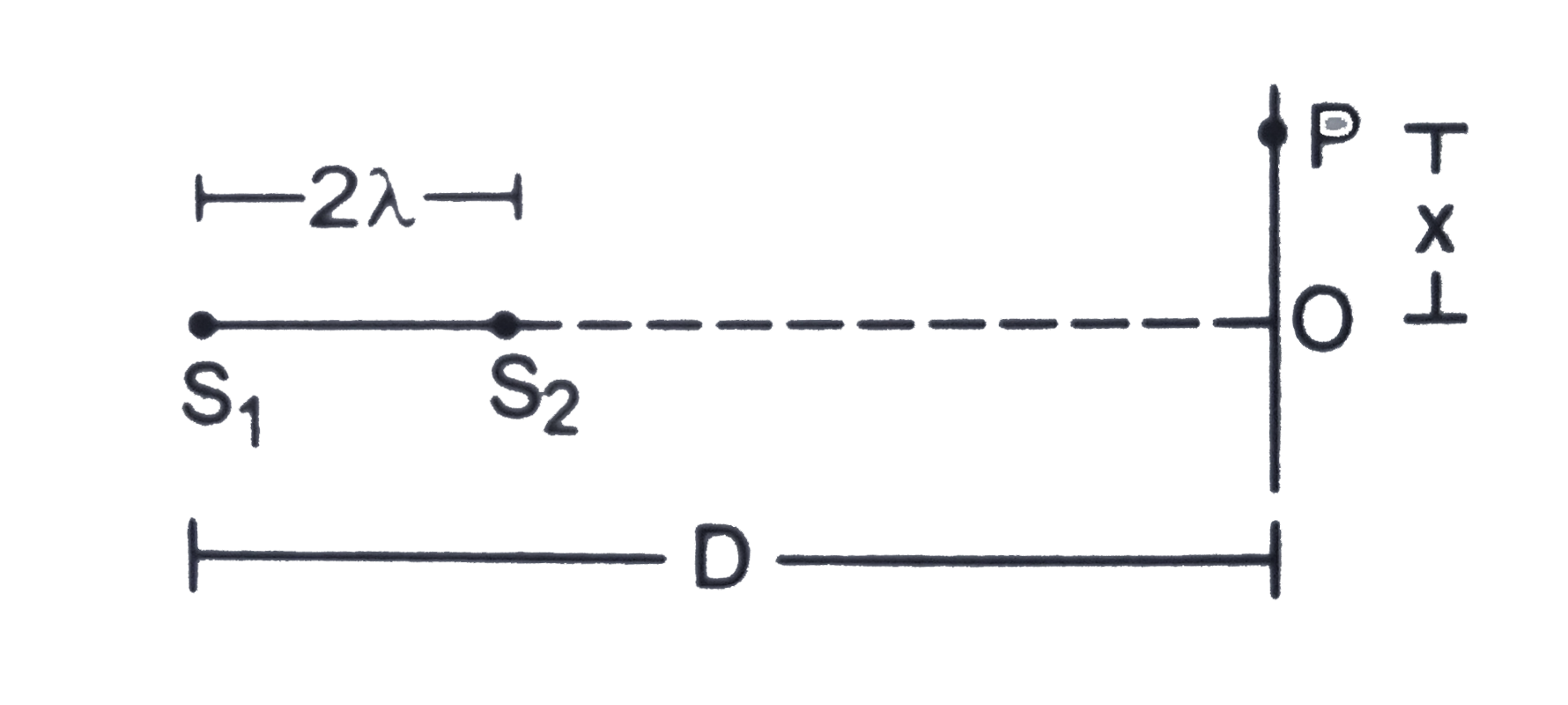
View SolutionA laser light of wavelength 660 nm is used to weld Retina detachment. If a laser pulse of width 60 ms and power 0.5 kW is used, the approximate number of photons in the pulse are (Take Planck's Constant, h=6.62×10−34Js)
View Solution