Match of following columns
Column-IColumn-II(A)Kinetic enery of aparticle in gravitationalfield is increasing(p)Work done bygravitational force shouldbe positive(B)Potential energy of aparticle in gravitationalfield is increasing(q)Work done by externalforce should be non-zero(C)Mechanical energy of aparticle in gravitationalfield is increasing(r)Work done bygravitational force shouldbe negative(s)Cannot say anything
The correct Answer is:(A→s,B→r,C→q)
To match the items in Column-I with those in Column-II, we need to analyze the relationships between kinetic energy, potential energy, mechanical energy, and the work done by gravitational and external forces in a gravitational field.
1. Understanding Kinetic Energy in a Gravitational Field:
- When a particle moves in a gravitational field, its kinetic energy can increase if it is falling or being accelerated by the field.
- As kinetic energy increases, potential energy decreases because the total mechanical energy (kinetic + potential) remains constant in a conservative field.
- Therefore, for (A) "Kinetic energy of a particle in gravitational field is increasing," we can conclude that the work done by the gravitational force should be positive.
- Match: (A) → (p)
2. Understanding Potential Energy in a Gravitational Field:
- Potential energy in a gravitational field is given by the formula U=−GMmr.
- As a particle moves deeper into the gravitational field (closer to the mass), its potential energy decreases (becomes more negative).
- Therefore, for (B) "Potential energy of a particle in gravitational field is increasing," the work done by an external force should be non-zero to counteract the gravitational force.
- Match: (B) → (q)
3. Understanding Mechanical Energy in a Gravitational Field:
- Mechanical energy is the sum of kinetic and potential energy. If kinetic energy increases, potential energy decreases, but the total mechanical energy remains constant in the absence of non-conservative forces.
- Therefore, for (C) "Mechanical energy of a particle in gravitational field is increasing," we cannot definitively say anything without additional information about external forces acting on the system.
- Match: (C) → (s)
4. Understanding Work Done by Gravitational Force:
- Work done by gravitational force is typically considered negative when the force opposes the motion (for example, lifting an object).
- Therefore, for the statement regarding work done by gravitational force being negative, we can conclude that it is related to the potential energy decreasing.
- Match: (B) → (r)
Final Matches:
- (A) → (p)
- (B) → (q)
- (C) → (s)
- When a particle moves in a gravitational field, its kinetic energy can increase if it is falling or being accelerated by the field.
- As kinetic energy increases, potential energy decreases because the total mechanical energy (kinetic + potential) remains constant in a conservative field.
- Therefore, for (A) "Kinetic energy of a particle in gravitational field is increasing," we can conclude that the work done by the gravitational force should be positive.
- Match: (A) → (p)
- Potential energy in a gravitational field is given by the formula U=−GMmr.
- As a particle moves deeper into the gravitational field (closer to the mass), its potential energy decreases (becomes more negative).
- Therefore, for (B) "Potential energy of a particle in gravitational field is increasing," the work done by an external force should be non-zero to counteract the gravitational force.
- Match: (B) → (q)
- Mechanical energy is the sum of kinetic and potential energy. If kinetic energy increases, potential energy decreases, but the total mechanical energy remains constant in the absence of non-conservative forces.
- Therefore, for (C) "Mechanical energy of a particle in gravitational field is increasing," we cannot definitively say anything without additional information about external forces acting on the system.
- Match: (C) → (s)
- Work done by gravitational force is typically considered negative when the force opposes the motion (for example, lifting an object).
- Therefore, for the statement regarding work done by gravitational force being negative, we can conclude that it is related to the potential energy decreasing.
- Match: (B) → (r)
- (A) → (p)
- (B) → (q)
- (C) → (s)
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (A) Chapter Exercises
68 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
Starting from the centre of the earth having radius R, the variation of g (acceleration due to gravity) is shown by
View SolutionWeightlessness in satellite is due to
View SolutionIf the dimensions of B2l2C are [MaLbTc], then the value of a+b+c is
[Here B,l and C represent the magnitude of magnetic field, length and capacitance respectively]
View SolutionA particle is projected with velocity 2(√gh), so that it just clears two walls of equal height h which are at a distance of 2h form each other. Show that the time of passing between the walls is 2(√hg). [Hint : First find velocity at height h. Treat it as initial velocity and 2h as the range. ]
View SolutionWhich of the following resonating structures is not correct for CO_2 ? overset(-):overset(..)underset(..)O-underset(I)C-=overset(+)O:harr:overset(+)underset(..)O-underset(II)C-=underset(..)Ooverset(-):harr overset(..)underset(..)O=underset(III)C=overset(..)underset(..)Oharr:overset(+)O-=underset(IV)C-underset(..)overset(..)Ooverset(-):harr
View SolutionArrange the following in the increasing order of their intermolecular forces underset((I))("Nylon 6") underset((II))("Neoprene") underset((III))("Polyvinyl chloride") .
View SolutionMatch of following columns {:(,"Column-I",,"Column-II"),("(A)",underset(underset("field is increasing")("particle in gravitational"))("Kinetic enery of a"),"(p)",underset(underset("be positive")("gravitational force should"))("Work done by")),("(B)",underset(underset("field is increasing")("particle in gravitational"))("Potential energy of a"),"(q)",underset("force should be non-zero")("Work done by external")),("(C)",underset(underset("field is increasing")("particle in gravitational"))("Mechanical energy of a"),"(r)",underset(underset("be negative")("gravitational force should"))("Work done by")),(,,"(s)","Cannot say anything"):}
View SolutionOrder of enolic content
(P)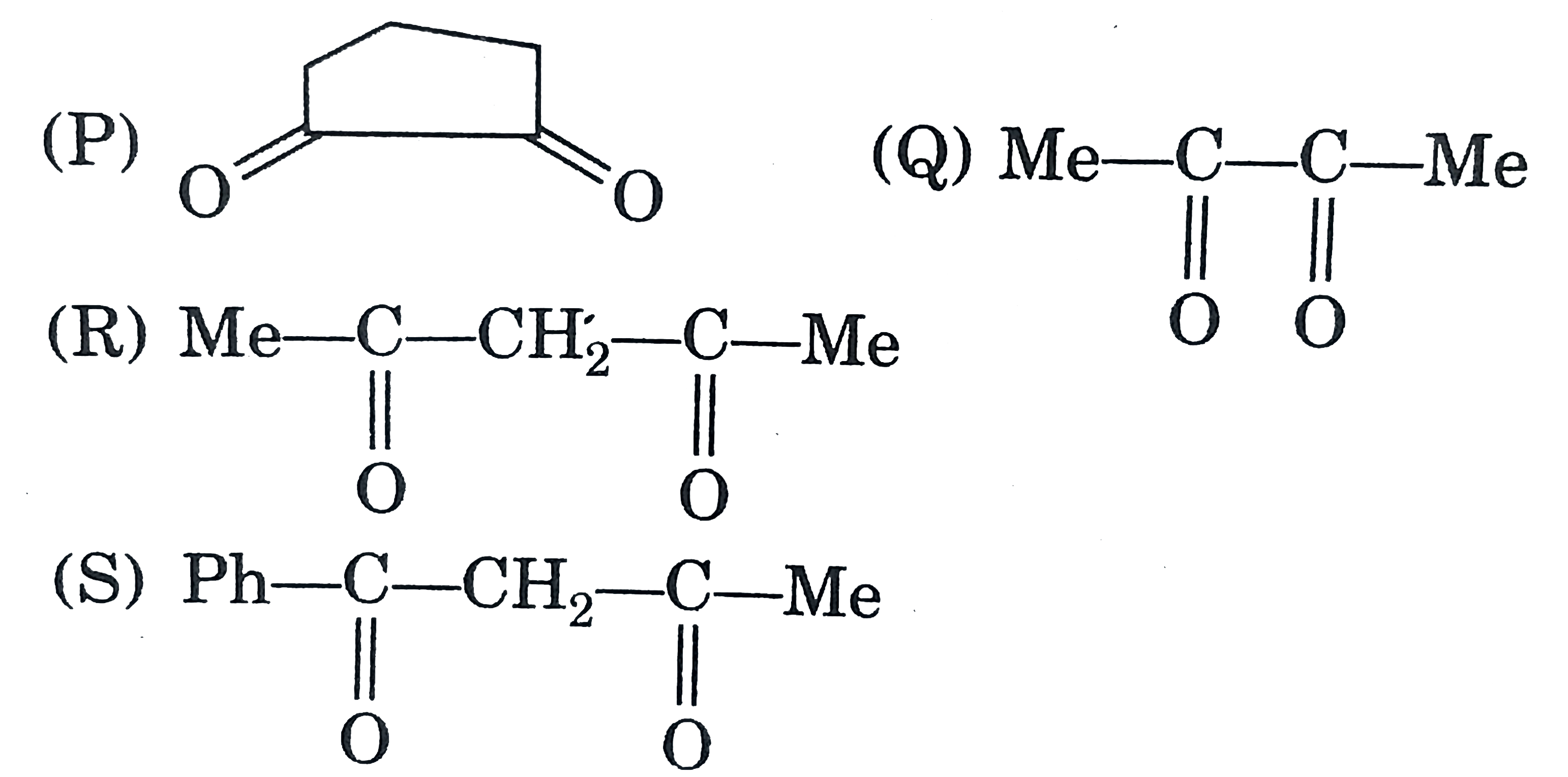
(Q) Me−C∣∣O−C∣∣O−Me
(S) Me−C∣∣O−CH2−C∣∣O−Me
View SolutionA nuclear reaction along with the masses of the particle taking part in it is as follows underset("amu")underset(1.002)A+underset("amu")underset(1.004)Btounderset("amu")underset(1.001)C+underset("amu")underset(1.003)D+QMeV The energy Q liberated in the reaction is
View SolutionA nuclear reaction along with the masses of the particle taking part in it is as follows
A1.002 amu+B1.004 amu→C1.001 amu+D1.003 amu+QMeV
the energy Q is liberated in the reaction is
View SolutionWhich of the following will be oxidised by HIO4?
(A) R−C∣∣O−C∣∣O−R
(B) R−C∣∣O−CH| OH−R
(C) R−CH−CH2−CH−R | | OH OH
(D) R−CH−CH−R | | OH OH
View Solutionनिम्नलिखित में से कौन ऐल्डोल संघनन देगा?
ऐसीटेल्डिहाइड I "बेन्जेल्डिहाइड"III("बेन्जेल्डिहाइड")underset(I)("ऐसीटेल्डिहाइड")" "underset(IV)underset("प्रोपेनेल्डिहाइड")underset(II)("क्लोरल")
View SolutionMatch Column-I with Column-II : {:("Column-I","Column-II"),("(1) Zero work done","(a) by gravitational force"),("(2) Positive work done","(b) opposite to gravitational force"),("(3) Negative work done","(c) by centripetal force"):}
View SolutionDetermine the correct configuration of following structures :
s−p|c|r−q(a)s−r|c|q−p(b)q−s|c|p−r(c)
p = I, q = Br, r = H, S = CI
View SolutionWhich alkyl halide from the following pairs would you expect to react more rapidly by an S_N2 mechanism ? Explain your answer. (i) underset((A))(CH_3CH_2Br) " or " underset((B))underset(Br)underset(|)(CH_3CH_2CHCH_3) (ii) underset((C))underset(Br)underset(|)(CH_3CH_2CHCH_3) " or " underset((D))underset(CH_3)underset(|)(H_3C-C-Br) (iii) underset((E))underset(CH_(3))underset(|)(CH_3CHCH_2CH_2Br) " or " underset((F))underset(CH_3)underset(|)(CH_3CH_2CHCH_2Br)
View Solution
