Mr. Verma (50kg) and Mr. Mathur (60kg) are sitting at the two extremes of a 4 m long boat (40 kg) standing still in water. To discuss a mechanics problem, they come to the middle of the boat. Neglecting frictioin with water how far does the boat move on the water during the process?
To solve the problem, we will use the principle of conservation of momentum and the concept of the center of mass. Here’s a step-by-step solution:
Step 1: Identify the masses and their positions
- Mass of Mr. Verma (m1) = 50 kg
- Mass of Mr. Mathur (m2) = 60 kg
- Mass of the boat (m3) = 40 kg
- Length of the boat = 4 m
- Initial positions:
- Mr. Verma is at position 0 m (one end of the boat)
- Mr. Mathur is at position 4 m (the other end of the boat)
- The boat is initially at rest.
Step 2: Calculate the initial center of mass (CM)
The center of mass (CM) of the system can be calculated using the formula:
xCM=m1x1+m2x2+m3x3m1+m2+m3
Where:
- x1=0 (position of Mr. Verma)
- x2=4 (position of Mr. Mathur)
- x3=2 (position of the boat's center, which is at 2 m)
Substituting the values:
xCM=(50×0)+(60×4)+(40×2)50+60+40
xCM=0+240+80150=320150=3215 m
Step 3: Understand the movement of the individuals
When Mr. Verma and Mr. Mathur move to the center of the boat, they will both move towards the middle (2 m from either end).
Step 4: Define the displacement of the boat
Let x be the displacement of the boat to the right.
- Mr. Verma moves to position 2+x (to the right).
- Mr. Mathur moves to position 2−x (to the left).
Step 5: Set up the equation for the center of mass
Since there are no external forces acting on the system, the center of mass must remain stationary. Therefore:
50(2+x)+60(2−x)+40x150=320150
Step 6: Solve for x
Expanding the equation:
50(2+x)+60(2−x)+40x=320
100+50x+120−60x+40x=320
Combining like terms:
220+30x=320
Subtracting 220 from both sides:
30x=100
Dividing by 30:
x=10030=103 m
Step 7: Conclusion
The boat moves x=103 m to the right.
- Mass of Mr. Verma (m1) = 50 kg
- Mass of Mr. Mathur (m2) = 60 kg
- Mass of the boat (m3) = 40 kg
- Length of the boat = 4 m
- Initial positions:
- Mr. Verma is at position 0 m (one end of the boat)
- Mr. Mathur is at position 4 m (the other end of the boat)
- The boat is initially at rest.
The center of mass (CM) of the system can be calculated using the formula:
xCM=m1x1+m2x2+m3x3m1+m2+m3
Where:
- x1=0 (position of Mr. Verma)
- x2=4 (position of Mr. Mathur)
- x3=2 (position of the boat's center, which is at 2 m)
xCM=(50×0)+(60×4)+(40×2)50+60+40
xCM=0+240+80150=320150=3215 m
When Mr. Verma and Mr. Mathur move to the center of the boat, they will both move towards the middle (2 m from either end).
Let x be the displacement of the boat to the right.
- Mr. Verma moves to position 2+x (to the right).
- Mr. Mathur moves to position 2−x (to the left).
Since there are no external forces acting on the system, the center of mass must remain stationary. Therefore:
50(2+x)+60(2−x)+40x150=320150
Expanding the equation:
50(2+x)+60(2−x)+40x=320
100+50x+120−60x+40x=320
Combining like terms:
220+30x=320
Subtracting 220 from both sides:
30x=100
Dividing by 30:
x=10030=103 m
The boat moves x=103 m to the right.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Question For short Answer
25 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -2
11 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -1
18 Videos
- CALORIMETRYBOOK - HC VERMA ENGLISHCHAPTER - CALORIMETRYEXERCISE - Short answer
9 Videos
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Question for short Answer
10 Videos
Similar Questions
Father (80 kg) and son (30 kg) are sitting at one of the ends of a 4 m long boat (40 kg) standing still on water. They start to shift slowly. Father stopped at centre of boat but son stopped at other end. Neglecting friction with water, how far does the boat move on the water during the process?
View SolutionA boat of mass 90 kg is floating in still water. A boy of mass 30 kg walks from one end to the other on it. If the length of the boat is 3 m, then the distance through which the boat will move is
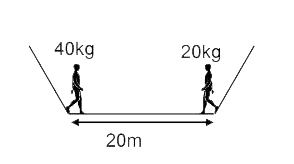
View SolutionTwo men of masses 40 kg and 20 kg are standing on a boat of mass 100 kg. Length of boat is 20m. Neglect the friction between water and boat. Find the displacement of the boat when both the persons reach at middle of boat.
View SolutionTwo persons of masses 55kg and 65kg respectively are at the opposite ends of a boat. The length of the boat is 3.0m and weights 100kg. The 55kg man walks up to the 65kg man and sits with him. If the boat is in still water the centre of mass of the system shifts by.
View SolutionTwo perons of masses 55 kg and 65 kg respectively, are at the opposite ends of a boat. The length of the boat is 3 m and weight 100 kg. The 55 kg man walks upto the 65 kg man and with him. If the boat is in still water the centre of mass of the system shifts by
View SolutionA man of mass 60 kg is standing on a boat of mass 140 kg, which is at rest in still water. The man is initially at 20 m from the shore. He starts walking on the boat for 4 s with constant speed 1.5 m/s towards the shore. The final distance of the man from the shore is
View SolutionA dog of mass 10 kg is standing on a flat 10 m long boat so that it is 20 m meters from the shore. It walks 8 m on the boat towards the shore and then stops. The mass of the boat is 40 kg and friction between the boat and the water surface is negligible. How far is the dog from the shore now ?

View SolutionA man weighing 70 kg is standing at the centre of a flat boat of mass 350 kg. The man who is at a distance of 10 m from the shore walks 2 m towards it and stops. How far will he be from the shore? Assume the boat to be of uniform thickness and neglect friction between boat and water?
View SolutionA boat of length 10m and mass 450kg is floating without motion in still water. A man of mass 50kg standing at one end of it walks to the other end of it and stops. The magnitude of the displacement of the boat in metres relative to ground is
View SolutionA boy having a mass of 40kg stands at one end A of a boat of length 2m at rest. The boy walks to the other end B of the boat and stops. What is the distance moved by the boat? Friciton exists between the feet of the boy and the surface of the boat. But the friction between the boat and the water surface may be neglected. Mass of the boat is 15kg.

View Solution
