Obtain an expression for the equivalent emf and internal resistance of two cells connected in parallel.Solution in Kannada
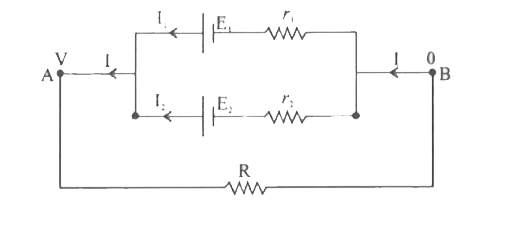
Let I1,I2 represent branch currents .
Let V be the common potential , so that ,
I1=E1−Vr1,I2=E2−Vr2
hence, I=E1−Vr1+E2−Vr2
i.e. I=(E1r1+E2r2)−V(1r1+1r2)
Comparing this with the terminal potential difference,
V=Eeq−Ireq
i.e., V=Eeq−I(Ireq)
For two cells in parallel combination,
(Eeq)p=E1r1+E2r21r1+1r2=E1r2+E2r1r1+r2
1(req)p=1r1+1r2 , and main current = I=EeqR+req
Note : (i) For n cells in parallel
V=⎡⎢⎣∑ni=1Eiri∑ni=11r1⎤⎥⎦−⎡⎣I∑ni=11ri⎤⎦
(Eeq)parallel=⎡⎢⎣∑ni=1Eiri∑ni=11ri⎤⎥⎦
(1req)p=n∑i−1(1ri)
(ii) For .n. number of identical cells
E-emf of each cell
r-internal resistance of each cell.
(Eeq)p=n(Er)n(1r)
i.e., (Eeq)p=E
and (1req)p=n(1r)
i.e. (req)p=rn
Main current , I=nER+nr and terminal potential difference across cells V=IR.
Topper's Solved these Questions
Similar Questions
A spherical hollow conductor is charged to -250V. If the radius of the conductor is 0.15m, then calculate
(i) Charge on the conductor.
(ii) Electric files intensity on the surface
(iii) Electric field intensity at the centre.
(iv) Electric potential difference between A and B at distances of 0.20 m & 0.25m from the centre respectively.
View SolutionFor a short magnetic dipole of magnetic moment 0.5 Am2. Find the magnetic field at a point ( a) 1 m on the axis and from the cetre of the magnet ( dipole ) ( b) 1 m on the equatorial line from the centre ( c) at an angle of 60∘ w.r. to the line joining the point and the centre of the dipole at distance 1 m.
View SolutionIf three cell are connected in parallel then equivalent emf……. and equivalent internal resistance is …..
View SolutionTwo cells of emfs 1.5 V and 2.0v having internal resistance 0.2 Sigma and 0.3 Sigma respectively are connected in parallel . Calculate the emf and internal resistance of the equivalent cell .
View SolutionTwo cells of emfs ε1andε2 and internal resistances r1andr2 respectively are connected in parallel . Obtain expressions for the equivalent (i) resistance and , (ii) emf of the combination.
View SolutionTwo cells of emfs l .5 V and 2.0 V having internal resistances 0.2 Omega and 0.3 Omega respectively are connected in parallel. Calculate the emf and internal resistance of the equivalent cell.
View SolutionIf a number of cells are connected in parallel then write their equivalent emf and internal resistance.
View SolutionObtain an expression for equivalent resistance of two resistors connected in parallel.
View SolutionObtain an expression for the equivalent emf and internal resistance of two cells connected in parallel.
View SolutionObtain an expression for the equivalent emf and internal resistance of two cells connected in parallel.
View SolutionTwo cells of emfs 1.5 V and 2.0 V having internal resistances 0.2Ω and 0.3Ω respectively are connected in parallel. Calculate the emf and internal resistance of the equivalent cell.
View SolutionTwo cells of emf 2ε and ε and internal resistance 2r and r respectively, are connected in parallel. Obtain the expressions for the equivalent emf and the internal resistance of the combination.
View SolutionObtain an expression for the equivalent emf and internal resistance of two cells connected in parallel.
View SolutionObtain the expression for the equivalent resistance for 3 resistors connected in parallel and also write the expression of equivalent resistance for connection of' n' resistors.
View SolutionWhat is parallel connections of cells? Derive the equivalent equation of parallel connections of two cells.
View Solution
