Obtain the expression of electric field at any point by continuous distribution of charge on a volume.Solution in Gujrati
Suppose a continuous charge distribution in space has a charge density ρ.
Choose any convenient origin O and let the position vector of any point in the charge distribution be →r.
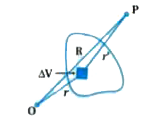
Divide the charge distribution into small volume elements of size ΔV.
The charge in a volume element ΔV is ρΔV.
Now, consider any general point P (inside or outside the distribution with position vector →R.
Electric field due to the charge ρΔV is given by Coulomb.s law.
→E=∑kρΔV(r.)2.ˆr
where r. is the distance between the charge element and P and f. is a unit vector in the direction from the charge element to P.
By the superposition principle, the total electric field,
→E=∫Vkρ.ΔV(r.)2ˆr=k≡ρΔVr2.ˆr
OR →E=k∫ρ.ΔVr−2.ˆr
In short, using Coulomb.s law and the superposition principle, electric field can be determined for any charge distribution, discrete or continuous or part discrete and part continuous.
Topper's Solved these Questions
- BOOK - KUMAR PRAKASHANCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION A QUESTIONS- ANSWERS (GAUSS.S LAW)3videos
ELECTRIC CHARGES AND FIELDS
- BOOK - KUMAR PRAKASHANCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION A QUESTIONS- ANSWERS (APPLICATION OF GAUSS.S LAW)1videos
ELECTRIC CHARGES AND FIELDS
- BOOK - KUMAR PRAKASHANCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SECTION A QUESTIONS- ANSWERS (DIPOLE IN UNIFORM EXTERNAL FIELD)4videos
ELECTRIC CHARGES AND FIELDS
- BOOK - KUMAR PRAKASHANCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section-D (MCQs asked in GUJCET/Board Exam)1videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - KUMAR PRAKASHANCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D MCQs (MCQs asked in Competitive Exams )38videos
ELECTROMAGNETIC INDUCTION
Similar Questions
Obtain Gauss's law from the flux associated with a sphere of radius r and charge 'q' at centre.
04:02View SolutionMention applications of Gauss's law.
06:37View SolutionWhat are polar and non-polar molecules ? Give their examples.
49:46View SolutionMass of photon in motion is ………
09:19View SolutionThree pure inductance each of 3 H are connected as shown in figure. The equivalent inductance of this connection between points A and B is ......
 01:16:24View Solution
01:16:24View SolutionElectric Field Due To Continuous Distribution Of Charge
07:03View SolutionGive the expression for electric field intensity at a point due to a discrete and continuous distribution of charges.
03:48View SolutionContinuous Charge Distribution & Electric Field due to that
03:39View SolutionObtain an expression for the electric field intenstiy at a point on the equatorial line of an electric dipole.
05:00View SolutionContinuous charge distribution | Line charge| Surface charge | Volume charge | Electric field due to line charge
05:12View SolutionHow do we determine the electric field due to a continuous charge distribution ? Explain. Electric field due to continous charge distribution
04:04View SolutionObtain the expression of electric field at any point by continuous distribution of charge on a line.
05:12View SolutionObtain the expression of electric field at any point by continuous distribution of charge on a surface.
14:20View SolutionObtain the expression of electric field by a plane of infinite size and with uniform charge distribution.
05:43View SolutionObtain the expression of electric field by thir spherical shell with uniform charge distribution at a point outside it.
02:11View Solution

