Question

Obtain the expression of electric field by a straight wire of infinite length and with linear charge density $\lambda$.

Explanation

Consider an infinitely long thin straight wire with uniform linear charge density `lambda`

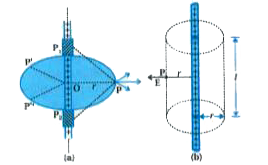
Suppose we take the radial vector from O to P and rotate it around the wire. The points P P., P" so obtained are completely equivalent with respect to the charged wire.
This implies that the electric field must have the same magnitude at these points.
The direction of electric field at every point must be radial (outward if `lambda gt 0`, inward `lambda lt 0` ).
Since the wire is infinite, electric field does not depend on the position of P along the length of the wire.
The electric field is everywhere radial in the plane cutting the wire normally and its magnitude depends only on the radial distance r.
Imagine a cylindrical Gaussian surface as shown in figure.
Since the field is everywhere radial, flux through the two ends of the cylindrical Gaussian surface is zero.
At the cylindrical part of the surface E is normal to the surface at every point and its magnitude is constant since it depends only on r.
The surface area of the curved part is 2nd, where I is the length of the cylinder.
Flux through the Gaussian surface, = flux through the curved cylindrical part of the surface
`= E xx 2pirl`
The surface includes charge equal to `lambdal`. Gauss.s law then gives,
`E xx 2pirl = (lambdal)/(epsilon_(0))`
`therefore E =lambda/(2pi epsilon_(0)r)`
`therefore vecE = lambda/(2pi epsilon_(0)r)hatn`
where `hatn` is the radial unit vector in the plane normal to the wire passing through the point.
`vecE` is directed outward if `lambda` is positive and inward if `lambda` is negative.
Note that it is impossible to find electric field at any point due to wire of infinite length, but here electric field is expressed at a point with effect of central part of wire and effect of ends is ignored.