Question

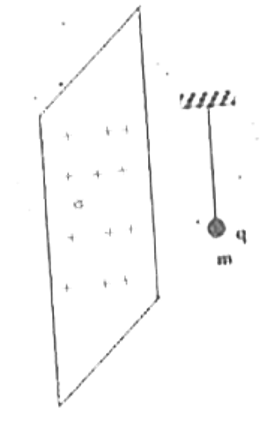
One end of a 10 cm long silk thread is fixed to a large vertical surface of a charged non conducting plate and the other end is fastened to a small ball having a mass of 10 g and charge of $4.0\times {10}^C$. In equilibrium, the thread make an angle of ${60}^0$ with the vertical. Find the surface charge density on the plate.

Explanation

To solve the problem step by step, we will analyze the forces acting on the charged ball and apply the principles of equilibrium and Gauss's law.

Step 1: Analyze the Forces Acting on the Ball
In equilibrium, the forces acting on the ball are:
1. The gravitational force (weight) acting downwards: \( F_g = mg \)
2. The tension in the thread acting at an angle of \( 60^\circ \) with the vertical: \( T \)
3. The electrostatic force due to the electric field created by the charged plate: \( F_e = QE \)

Step 2: Resolve the Tension into Components
The tension \( T \) can be resolved into two components:
- Vertical component: \( T \cos(60^\circ) \)
- Horizontal component: \( T \sin(60^\circ) \)

Step 3: Write the Equilibrium Conditions
For vertical equilibrium:
\( T \cos(60^\circ) = mg \)
For horizontal equilibrium:
\( T \sin(60^\circ) = QE \)

Step 4: Substitute the Electric Field Expression
The electric field \( E \) due to an infinite charged plate is given by:
\( E = \frac{\sigma}{2\epsilon_0} \)
where \( \sigma \) is the surface charge density and \( \epsilon_0 \) is the permittivity of free space.

Step 5: Substitute \( E \) into the Horizontal Force Equation
Substituting the expression for \( E \) into the horizontal equilibrium equation gives:
\( T \sin(60^\circ) = Q \left(\frac{\sigma}{2\epsilon_0}\right) \)

Step 6: Solve for Tension \( T \)
From the vertical equilibrium equation:
\( T = \frac{mg}{\cos(60^\circ)} \)

Step 7: Substitute \( T \) into the Horizontal Force Equation
Substituting \( T \) into the horizontal force equation:
\( \frac{mg}{\cos(60^\circ)} \sin(60^\circ) = Q \left(\frac{\sigma}{2\epsilon_0}\right) \)

Step 8: Simplify and Solve for Surface Charge Density \( \sigma \)
Now, we can rearrange the equation to solve for \( \sigma \):
\( \sigma = \frac{2mg \sin(60^\circ) \cos(60^\circ)}{Q} \epsilon_0 \)

Step 9: Substitute Known Values
Given:
- \( m = 10 \, \text{g} = 0.01 \, \text{kg} \)
- \( g = 10 \, \text{m/s}^2 \)
- \( Q = 4.0 \times 10^{-6} \, \text{C} \)
- \( \epsilon_0 = 8.85 \times 10^{-12} \, \text{C}^2/\text{N m}^2 \)
- \( \sin(60^\circ) = \frac{\sqrt{3}}{2} \)
- \( \cos(60^\circ) = \frac{1}{2} \)

Substituting these values:
\( \sigma = \frac{2 \times 0.01 \times 10 \times \frac{\sqrt{3}}{2} \times \frac{1}{2}}{4.0 \times 10^{-6}} \times 8.85 \times 10^{-12} \)

Step 10: Calculate the Value of \( \sigma \)
Calculating the above expression gives:
\( \sigma = \frac{0.01 \times 10 \times \sqrt{3} \times 8.85 \times 10^{-12}}{4.0 \times 10^{-6}} \)

After performing the calculations, we find:
\( \sigma \approx 7.5 \times 10^{-7} \, \text{C/m}^2 \)

Final Answer
The surface charge density on the plate is approximately:
\( \sigma \approx 7.5 \times 10^{-7} \, \text{C/m}^2 \)

---