One end (say B) of a massless spring having force constant k is attached to a block lying on a smooth surface while the other end A is pulled by an external force At some instant the velocities of end A and B of the spring are vA and vB respectively. If the energy of the spring is increasing at the rate of PJ/s find the instantaneous tension and stretch in the spring.
Let l be the natural length of the spring and xA and xB be the position of ends A and B at time t, then stretched length of the spring will be
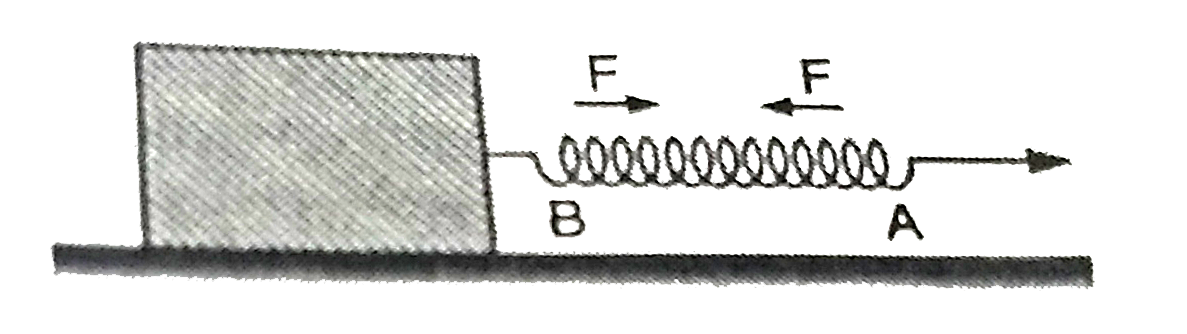
l'=xA−xB
and so the stretch
x=l'−l=(xA−xB−l)
and so, F=kx=k(xA−xB−l)
and U=12kx2=12k(xA−xB−l)2....(ii)
Diferentiating eqn (ii) with respect to time,
dUdt=k(xA−xB−l)(dxAdt−dxBdt) ...(iii)
But as dUdt=P,dxAdt=vAanddxBdt=vB(given)
So, Eqn (iii) in the light of (i) reduces to
P=F(vA−vB)
So, tension F=P(vA−vB)
and Strectch x=Fk=Pk(vA−vB)
Topper's Solved these Questions
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Problem for practice
30 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Objective Questions
134 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Comprehension
12 Videos
- BASIC MATHEMATICSBOOK - GRB PUBLICATIONCHAPTER - BASIC MATHEMATICSEXERCISE - Problems For Practice
35 Videos
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Comprehension type
11 Videos
Similar Questions
A block of mass 2 kg is connect to an ideal spring and the system is placed on a smooth horizontal surface. The spring is pulled to move the block and at an instant the speed of end A of the spring and speed of the block were measured to be 6 m/s and 3 m/s respectively. At this moment the potential energy stored in the spring is increasing at a rate of 15 J/s. Find the acceleration of the block at this instant.

View SolutionA block of mass M is placed on a smooth horizontal surface and it is pulled by a light spring as shown in the diagram. If the ends A and B of the spring are moving with 4 ms−1 and 2 ms−1 respectively and the rate at which spring energy is increasing is 20 Js−1. then what is the value of spring force (in N)?
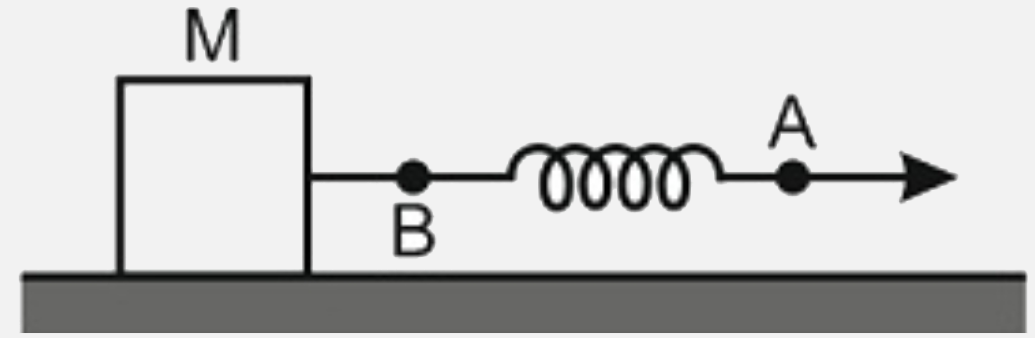
View Solution
Knowledge Check
Two identical massless springs A and B consist spring constant kA and kB respectively. Then :
Ait they are compressed by same force, work done on A is more expanded when kA>kBBif they are compressed by same amount, work done on A is more expanded when kA<kBCif they are compressed by same amount, work done on A is more expanded when kA>kBDboth (1) and (2) are correctAn ideal spring having force constant k is suspended from the rigid support and a block of mass M is attached to its lowe end. The mass is released from the natural length of the spring. Then the maximum exiension in the spring is
A4mgkB2MgkCMgkDMg2kA spring of force constant K rests on a smooth floor, with one end fixed to a wall. A block of mass m hits the free end of the spring with velocity v. The maximum force exerted by the spring on the wall is
Av√(mk)Bmv√kCm√(vk)Dk√(mv)
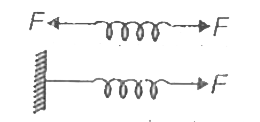
Figure shows tow cases. In first case a spring (spring constant K) is pulled by two equal and opposite forces F at both ends and in second case is pulled by a force F at one end. Extensions (x) in the springs will be
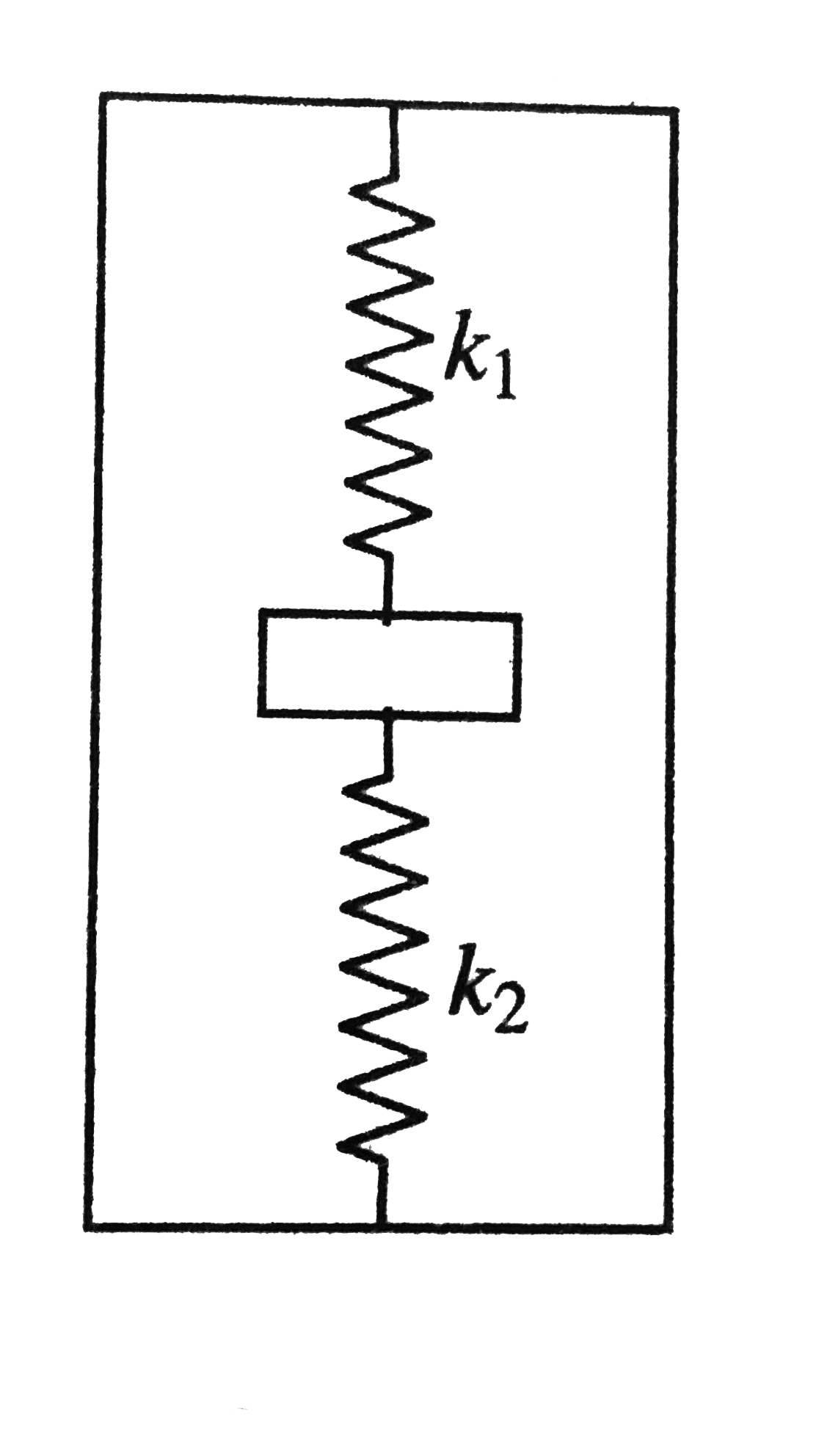
View SolutionOne end of a spring of force constant k1 is attached to the ceiling of an elevator. A block of mass 1.5kg is attached to the other end. Another spring of force constant k2 is attached to the bottom of the mass and to the floor of the elevator as shown in figure. At equilibrium, the deformation in both the spring is equal and is 40cm. If the elevator moves with constant acceleration upward, the additional deformation in both the spring is 8cm. Find the elevator's accelerationn ( g=10ms−2).
View SolutionOne end of a light spring of spring constant k is fixed to a wall and the other end is tied to a block placed on a smooth horizontal surface. In a displacement, the work by the spring is 12kx2. The possible cases are
View SolutionA block attached with an ideal spring is kept on a smooth horizontal surface. Now the free end of the spring is pulled with a constant velocity u horizontally. Then the maximum energy stored in the spring and bock system during subsequent motion is :
View SolutionOne end of a light spring of spring constant k is fixed to a wall and the other end is tied to a block placed on a smooth horizontal surface. In a displacment, the work done by the spring is +(12)kx2. The possible cases are.
View Solution
