Pendulum A is a physical pendulum made from a thin, rigid and uniform rod whose length is d. One end of this rod is attached to the ceiling by a frictionless hinge, so that the rod is free to swing back and forth. Pendulum B is a simple pendulum whose length is also d. Obtain the ratio TATB of their periods for small angle oscillations.
The correct Answer is:A
To find the ratio of the periods of pendulum A (a physical pendulum) and pendulum B (a simple pendulum), we can follow these steps:
Step 1: Determine the period of Pendulum A (Physical Pendulum)
For a physical pendulum, the period TA is given by the formula:
TA=2π√IMgd
where:
- I is the moment of inertia about the point of suspension,
- M is the mass of the pendulum,
- g is the acceleration due to gravity,
- d is the distance from the point of suspension to the center of mass.
For a uniform rod of length d pivoted at one end, the moment of inertia I is:
I=13Md2
The center of mass of the rod is located at d2 from the pivot point. Thus, we can substitute I into the period formula:
TA=2π
⎷13Md2Mgd=2π√d3g
Step 2: Determine the period of Pendulum B (Simple Pendulum)
For a simple pendulum, the period TB is given by the formula:
TB=2π√Lg
where L is the length of the pendulum. In this case, L=d:
TB=2π√dg
Step 3: Calculate the ratio TATB
Now, we can find the ratio of the periods:
TATB=2π√d3g2π√dg
The 2π and √d terms cancel out:
TATB=√13√1=√13=1√3≈0.577
Final Result
Thus, the ratio of the periods of pendulum A to pendulum B is:
TATB=√23≈0.816
For a physical pendulum, the period TA is given by the formula:
- I is the moment of inertia about the point of suspension,
- M is the mass of the pendulum,
- g is the acceleration due to gravity,
- d is the distance from the point of suspension to the center of mass.
⎷13Md2Mgd=2π√d3g
For a simple pendulum, the period TB is given by the formula:
Now, we can find the ratio of the periods:
Thus, the ratio of the periods of pendulum A to pendulum B is:
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Single Correct
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 More Than One Correct
8 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Single Correct
24 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
A vertical rod is rotating about its axis with a uniform angular speed ω . A simple pendulum of length l is attached to its upper end what is its inclination with the rod ?
View SolutionTwo compound pendulums are made of :
a disc of radius r and
(b) A uniform rod of length L. Find the minimum possible time period and distance between centre and point of suspension in each case.
View Solution
Knowledge Check
There is a rod of length l and mass m. It is hinged at one end to the ceiling. The period of small oscillation is
AT=2π√2l3gBT=π√l3gCT=2π√l3gDT=2π√lgA simple pendulum has time period T. A uniform rod, whose length is the same as that of the pendulum, undergoes small oscillations about its upper end. Its time period of oscillation will be -
A<TBTC>TDmay be (A), (B) or (C) depending on whether T is < equal to or >2secondsA pendulum is formed by pivotting a long thin rod of length L and mass m about a point P on the rod which is a distance d above the centre of the rod as shown.

The time period of this pendulum when d = L/2 will beA2π√2l3gB2π√3l2gC4π√l3gD2π3√2lg
A thin uniform rod of length l is pivoted at its upper end. It is free to swing in a vertical plane. Its time period for oscillation of small amplitude is
View SolutionA pendulum is formed by pivoting a long thin rod of length L and mass m about a point P on the rod which is a distance d above the centre of the rod as shown.
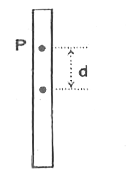
The time period of this pendulum when d = L/2 will be
View SolutionA pendulum is formed by pivoting a long thin rod of length L and mass m about a point P on the rod which is a distance d above the centre of the rod as shown.
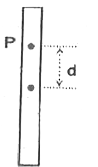
Time period will be minimum when d is equal to
View SolutionA pendulum is formed by pivotting a long thin rod of length L and mass m about a point P on the rod which is a distance d above the centre of the rod as shown.

As d changes from L/2 to zero
View SolutionA thin uniform rod of length L=100cm is to be pivoted about some point passing through the rod is allowed to swing as a physical pendulum. For this situation mark the correct statement (s) [take g=10m/s2]
View Solution