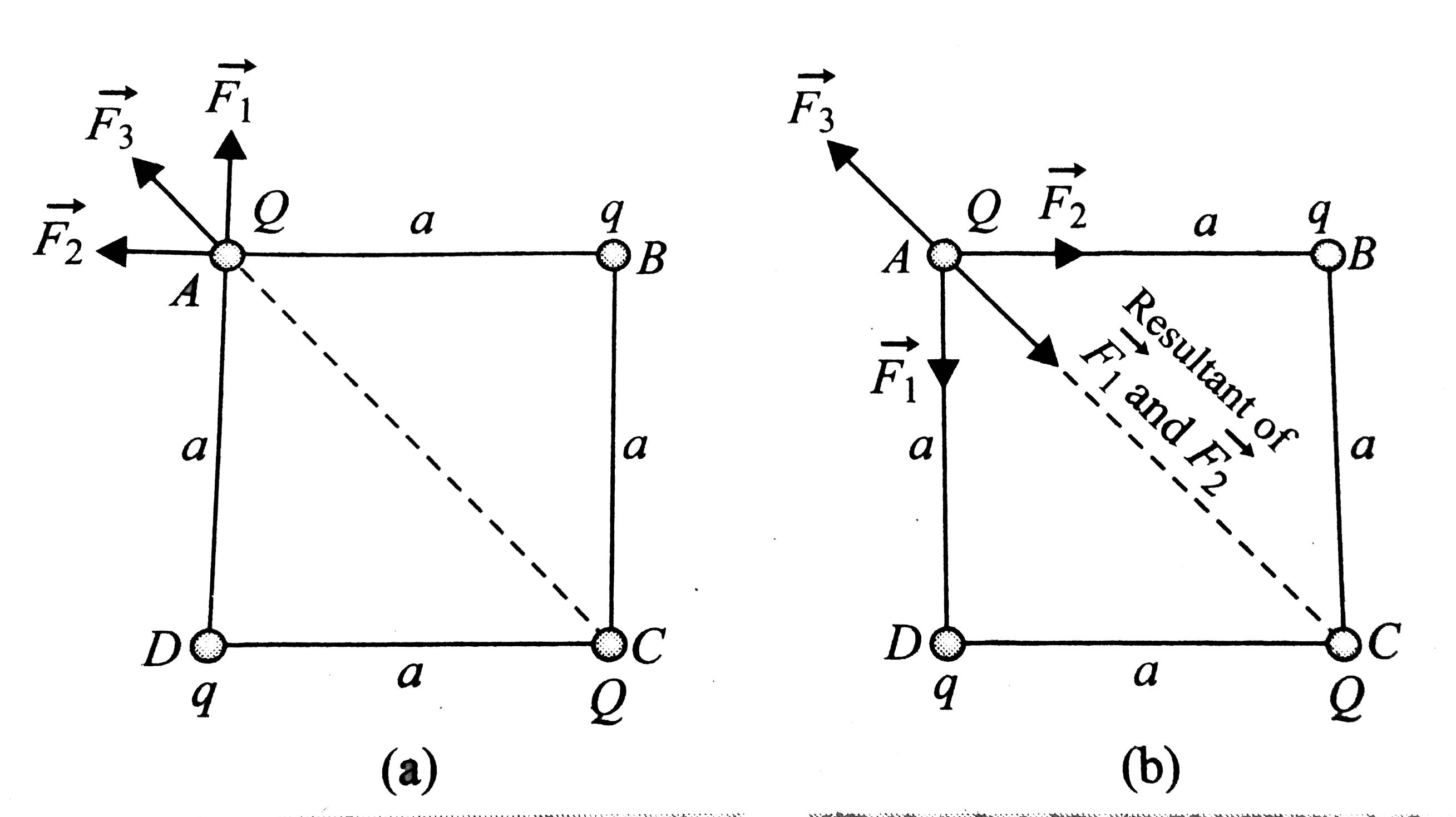
Point charge are placed at the verticas of a squre of side a as shown in fig. What should be the sign of charge q and magnitude of the ratio |q/Q| so that
(i) net force on each Q is zero?
(ii) net force on each q is zero?
Is it possible that the entire system could be in electrostatic equilibrium?

Consider the force action on charge Q placed at (shown in fig. )
Case I. Let the charge q and Q be of same sign.
here,
(F1)=14πε0qQa2 (force of q at D on Q at A)
 ,
, 
(F2)=14πε0qQa2 (force of q atB on Q at A)
(F3)=14πε0qQa2 (force of q atC on Q at A)
In fig. the resultant of force −→F1 and −→F2 will along −→F3 so that the net force on Q can not be zero. Hence, q and Q have to be of opposite signs.
Case II. Let the charges q and Q be of opposite signs. In this case, as shown in fig. resultant of −→F1 and −→F2 will be opposite to −→F3 so that it bexomes possible to obtain a condition of zero net force. Let us write →FR=→F1+→F2. so
√F21+F22=14πε0qQa2√2
The direction of →FR will be along AC (→FR, being the resultant of force of equal magnitude, bisects the angle between the two). →FR and →F3 are omn opposite directions. Theat force on Q can be zero if their magnitudes are also equal. i,e.
14πε0qQa2√2=14πε0QQ2a2 or Q4πε0(q√2−Q2)=0
or q=Q2√2 or ∣∣∣qQ∣∣∣=12√2{Q≠0}
Therefore, the sign of q should be the negative of Q.
(ii) Consider now the forces acting on charge q placed at B. In a similar manner, as dicussed in (i) , for the net force on q to be zero. q and Q have to be of opposite signs. This is also shown in the given figure.
F1=14πε0qQa2 (force of Q at A on q at B)
F2=14πε0qQa2 (force of Q at C on q at B)
F3=14πε0qQa2 (force of q at D on qat B)
 ,
, 
From fig. we can write
→FR=→F1+→F2
∴FR=√F21+F22=14πε0Qqa2√2
The resultant of →F1 and →F2 i.e →FR is opposite to →F3 . Net force can become zero if their magnitudes are also equal i.e.
14πε0Qqa2√2=14πε0q22a2 or q4πε0a2[√2Q−q2]=0
or Q=q2√2 or ∣∣∣qQ∣∣∣=2√2{q≠0}
Therefore, the sign of q should be negative of Q. In this case, we need not to repeat the calculation as the present situation id same as the previous one, we can directly write |q/Q|=2√2. The entire system cannot be in equilibrium since both conditions i.e. q=−Q/2√2 and Q=−q/2√2 cannot be satisfied together.
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Solved examples
10 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Exercises
58 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
Similar Questions
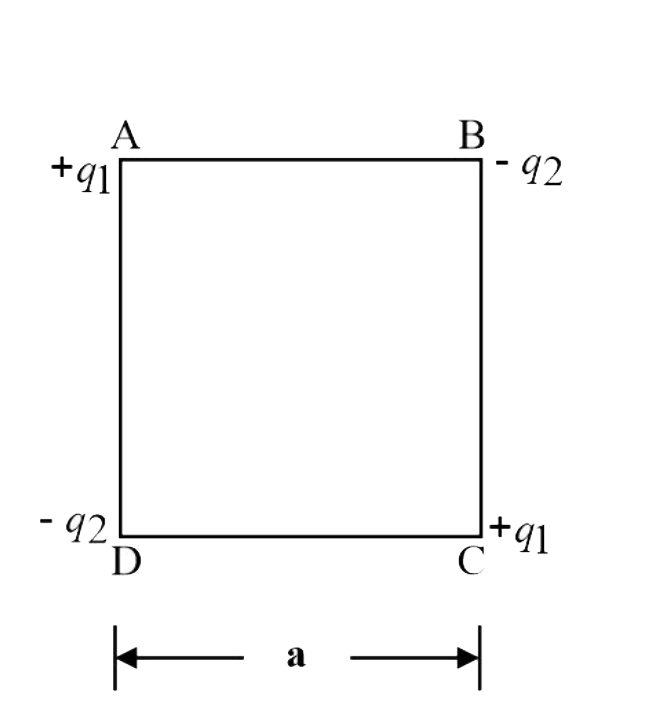
Charges are placed at the corners of a square of side a as shown in the following figure. The charged particle placed at A is in equilibrium. The ratio q1q2 is
View SolutionA charge Q is placed at the centre of the line joining two point charges +q and +q as shown in figure. The ratio of charges Q and q is

View Solution
Knowledge Check
Consider the charges q,q and -q placed at the vertices of an equilateral triangle of each side l. What is the force on each charge ?
Aq24√2πε0l2B−q24πε0l2Cq24πε0l2Dzero
Point charge are placed the corners of square of side 'a'. The value and nature of q can be best represented, to make the net force on Q zero as -

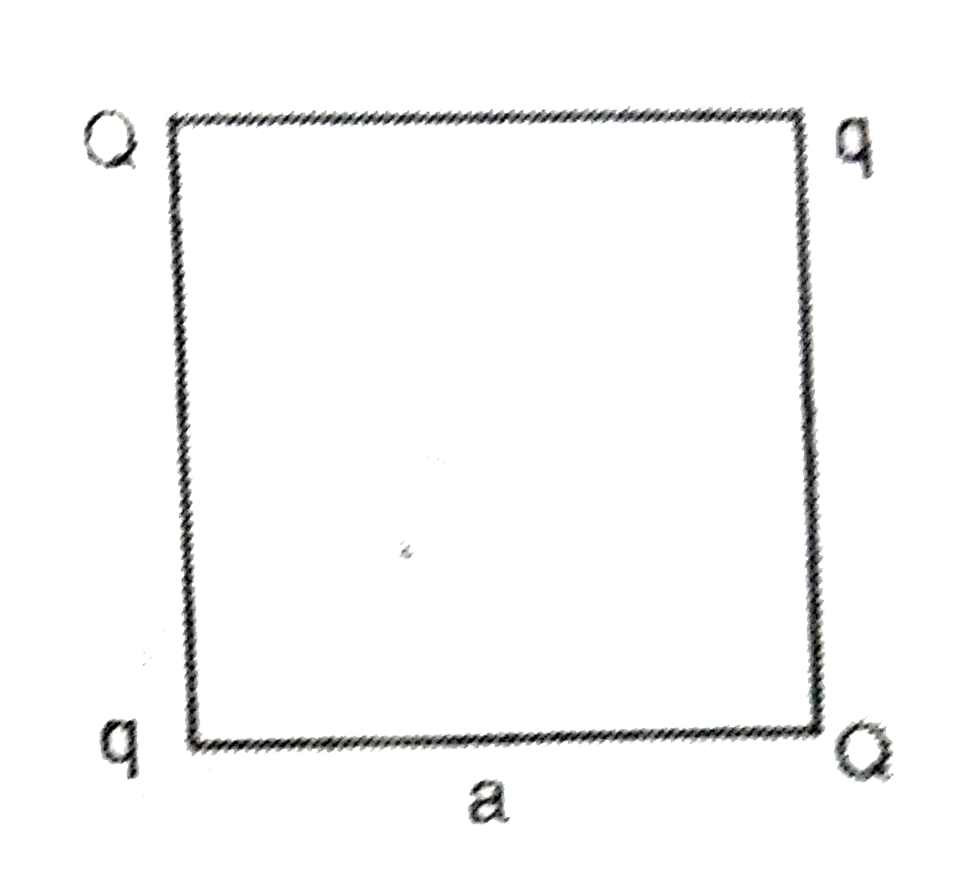
View SolutionFour point charges Q, q, Q and q are placed at the corners of a square of side' a' as shown in the figure.
Find the .
(a) resultnat electric force on a charge Q and .
(b) potential energy of this system.
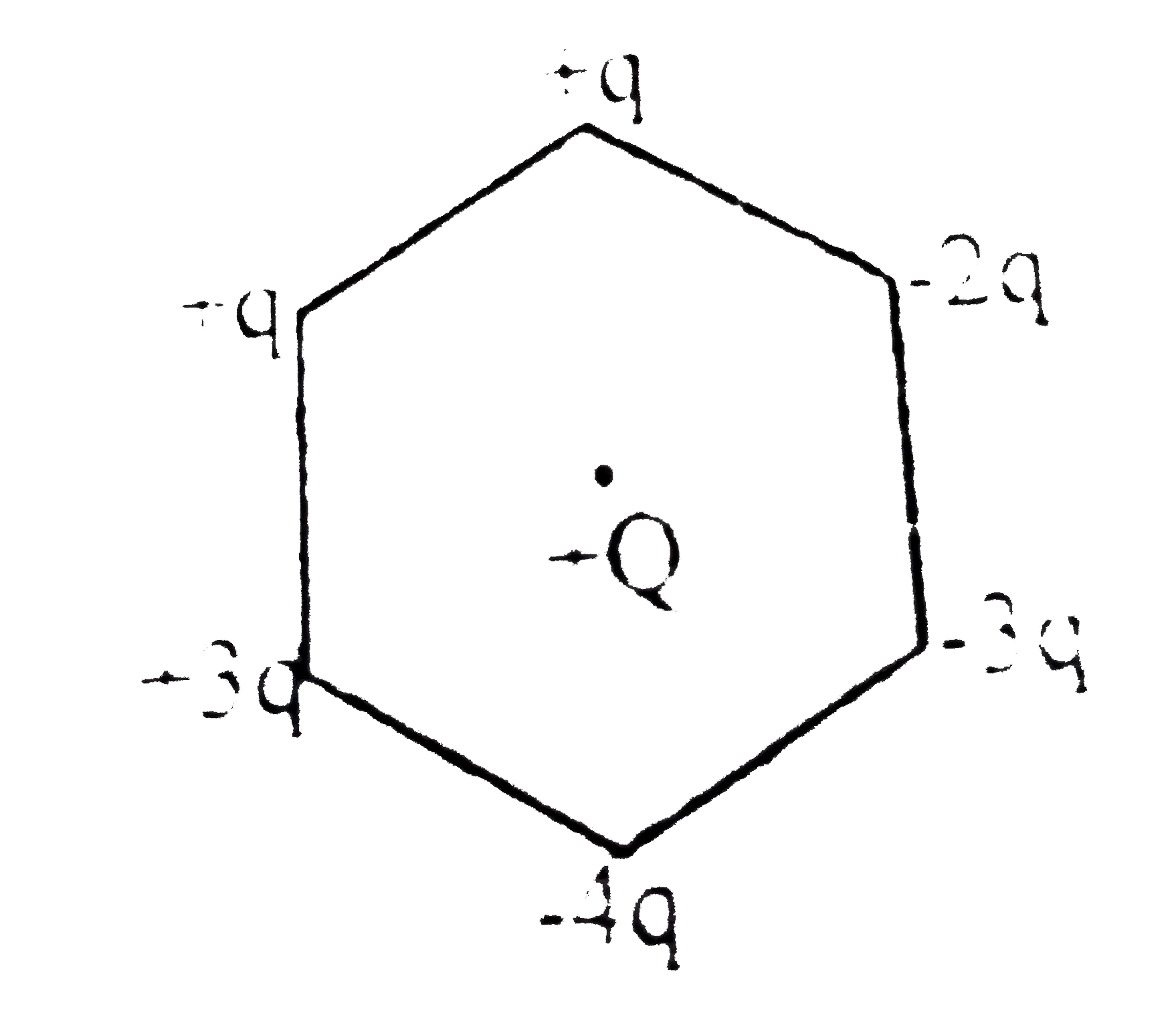
View SolutionSix charges are kept at the vertices of a regular hexagon as shown in the figure. If magnitude of force applied by +Q on +q charge is F, then net electric force on the +Q is nF. Find the value of n.
View SolutionThree charges Q,(+q) and (+q) are placed at the vertices of an equilateral triangle of side l as shown in the figure. It the net electrostatic energy of the system is zero, then Q is equal to

View SolutionThree charges Q,(+q) and (+q) are placed at the vertices of an equilateral triangle of side l as shown in the figure. It the net electrostatic energy of the system is zero, then Q is equal to

View SolutionFive point charge (+q each) are placed at the five vertices of a regular hexagon of side 2a.what is the magnitude of the net electric field at the centre of the hexazon?
View SolutionFour identical charges each .q. are placed at four corners of a square of side .a.. Find the charge to be placed at the centre of the square so that the system of charges is in equilibrium
View Solution
