There is a uniform electric field of strength 103V/m along y-axis. A body of mass 1g and charge 10−6C is projected into the field from origin along the positive x-axis with a velocity 10m/s. Its speed in m/s after 10s is (Neglect gravitation)
10
5√2
10√2
20
The correct Answer is:C
To solve the problem step by step, we need to analyze the motion of the charged body in the electric field. Here’s how we can approach it:
Step 1: Understand the Problem
We have a uniform electric field of strength E=103V/m directed along the y-axis. A body with mass m=1g=10−3kg and charge q=10−6C is projected from the origin along the positive x-axis with an initial velocity ux=10m/s.
Step 2: Calculate the Force Acting on the Body
The force F acting on the body due to the electric field is given by:
F=qE
Substituting the values:
F=(10−6C)(103V/m)=10−3N
Step 3: Calculate the Acceleration
Using Newton's second law, the acceleration a of the body can be calculated as:
a=Fm
Substituting the values:
a=10−3N10−3kg=1m/s2
Step 4: Determine the Velocity in the Y-Direction After 10 Seconds
Since the body starts from rest in the y-direction, the initial velocity uy=0m/s. We can use the first equation of motion to find the final velocity vy in the y-direction after t=10s:
vy=uy+at
Substituting the values:
vy=0+(1m/s2)(10s)=10m/s
Step 5: Calculate the Net Speed After 10 Seconds
The body has a constant velocity in the x-direction and a velocity in the y-direction after 10 seconds. The final velocities are:
- vx=10m/s (in the x-direction)
- vy=10m/s (in the y-direction)
The net speed v can be calculated using the Pythagorean theorem:
v=√v2x+v2y
Substituting the values:
v=√(10m/s)2+(10m/s)2=√100+100=√200=10√2m/s
Final Answer
The speed of the body after 10 seconds is 10√2m/s.
---
We have a uniform electric field of strength E=103V/m directed along the y-axis. A body with mass m=1g=10−3kg and charge q=10−6C is projected from the origin along the positive x-axis with an initial velocity ux=10m/s.
The force F acting on the body due to the electric field is given by:
F=qE
Substituting the values:
F=(10−6C)(103V/m)=10−3N
Using Newton's second law, the acceleration a of the body can be calculated as:
a=Fm
Substituting the values:
a=10−3N10−3kg=1m/s2
Since the body starts from rest in the y-direction, the initial velocity uy=0m/s. We can use the first equation of motion to find the final velocity vy in the y-direction after t=10s:
vy=uy+at
Substituting the values:
vy=0+(1m/s2)(10s)=10m/s
The body has a constant velocity in the x-direction and a velocity in the y-direction after 10 seconds. The final velocities are:
- vx=10m/s (in the x-direction)
- vy=10m/s (in the y-direction)
v=√v2x+v2y
Substituting the values:
v=√(10m/s)2+(10m/s)2=√100+100=√200=10√2m/s
The speed of the body after 10 seconds is 10√2m/s.
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:COULOMB LAW AND ELECTRIC FIELDExercise:Multiple Correct Answer Type
Explore 1 Video
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICS ENGLISHChapter:CENGAGE PHYSICS DPPExercise:subjective type
Explore 51 Videos
- ELECTRIC CURRENT & CIRCUITSBook:CENGAGE PHYSICS ENGLISHChapter:ELECTRIC CURRENT & CIRCUITSExercise:Kirchhoff s law and simple circuits
Explore 15 Videos
Similar Questions
A uniform cube of mass m and edge a moves on a horizontal surface along the positive x-axis, with initial velocity v0. Then
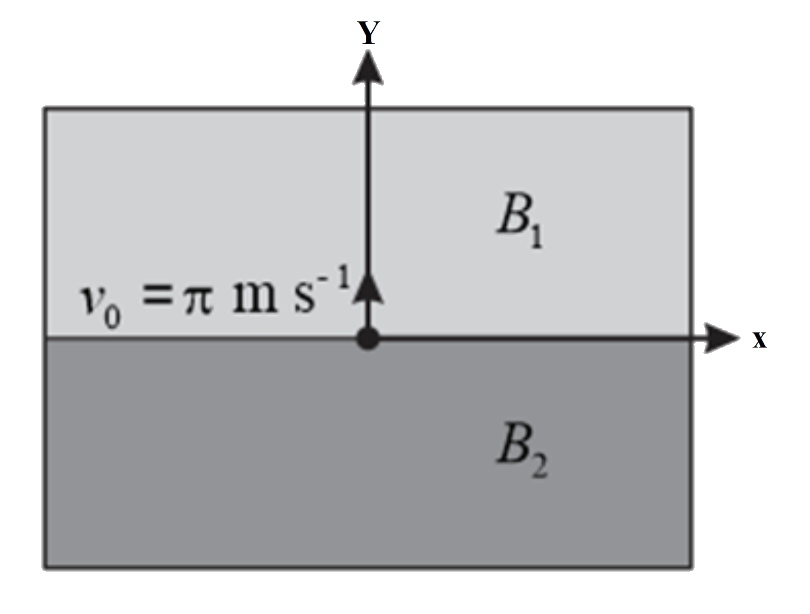
View SolutionIn the XY- plane , the region y>0 has a uniform magnetic field B1ˆk and the region y<0has another uniform magnetic field B2ˆk. A positively charged particle is projected from the origin along the positive y- axis with speed v0=πms−1 at t=0 , as shown in the figure . Neglect gravity in this problem . Let t=T be the time when the particle crosses the X- axis from below for the first time . If B2=4B1, the average speed to the particle , in ms−1, along the x- axis in the time interval T is __________ .
View SolutionIn a certain region of space, there exists a uniform and constant electric field of magnitude E along the positive y-axis of a coordinate system. A charged particle of mass m and charge -q (qgt0) is projected form the origin with speed 2v at an angle of 60∘ with the positive x-axis in x-y plane. When the x-coordinate of particle becomes √3mv2/qE a uniform and constant magnetic. field of strength B is also switched on along positive y-axis.
x-coordinate of the particle as a function of time after the magnetic field is switched on is
View SolutionIn a certain region of space, there exists a uniform and constant electric field of magnitude E along the positive y-axis of a coordinate system. A charged particle of mass m and charge -q (qgt0) is projected form the origin with speed 2v at an angle of 60∘ with the positive x-axis in x-y plane. When the x-coordinate of particle becomes √3mv2/qE a uniform and constant magnetic field of strength B is also switched on along positive y-axis.
Velocity of the particle just before the magnetic field is switched on is
View SolutionThe potential due to a short electric field dipole moment2×10−6 C-m along its axis point 4 m from dipole is
View SolutionThere exist uniform magnetic and electric fields of manitudes 1T and 1Vm−1 respectively, along positive y-axis. A charged particle of mass 1kg and charge 1C is having velocity 1ms−1 along x-axis and is at origin at t=0. Then, the coordinates of the particle at time πs will be
View SolutionThere exist uniform magnetic and electric fields of manitudes 1T and 1Vm−1 respectively, along positive y-axis. A charged particle of mass 1kg and charge 1C is having velocity 1ms−1 along x-axis and is at origin at t=0. Then, the coordinates of the particle at time πs will be
View SolutionAn electric field is acting vertically upwards . A particle of mass 1 mg and charge −1μC is projected with a velocity 20m/s at an angle 45∘ with the horizontal . Its horizontal range is 10 m, then the intensity of electric field is (g=10m/s2)
View SolutionIn a certain region of space, there exists a uniform and constant electric field of strength E along x-axis and uniform constant magnetic field of induction B along z-axis. A charge particle having charge q and mass m is projected with speed v parallel to x-axis from a point (a, b, 0). When the particle reaches a point( 2a, b/2, 0) its speed becomes 2v. Find the value of electric field strength in term of m, v and co-ordinates.
View SolutionA body is projected horizontally from the top of a tower with a velocity of 30 m/s. The velocity of the body 4 seconds after projection is (g = 10ms−2)
View Solution