Two short dipoles pˆk and P2ˆk are located at (0,0,0) & (1m,0,2m) respectivley. The resultant electric field due to the two dipoles at the point (1m,0,0) is
9P32πε0ˆk
−7P32πε0ˆk
7P32πε0ˆk
none of these
The correct Answer is:B
To find the resultant electric field at the point (1m, 0, 0) due to the two dipoles located at (0, 0, 0) and (1m, 0, 2m), we will follow these steps:
Step 1: Identify the Dipoles and Their Positions
- The first dipole, →p1=P^k, is located at the origin (0, 0, 0).
- The second dipole, →p2=P2^k, is located at (1m, 0, 2m).
Step 2: Calculate the Electric Field due to the First Dipole
The electric field →E1 due to a dipole at a point in space is given by the formula:
→E=14πϵ0⋅2→pr3
where →p is the dipole moment and r is the distance from the dipole to the point of interest.
For the first dipole at (0, 0, 0):
- The distance r1 from (0, 0, 0) to (1, 0, 0) is 1m.
- Therefore, the electric field →E1 at (1, 0, 0) is:
→E1=14πϵ0⋅2P^k(1)3=2P4πϵ0^k=P2πϵ0^k
Step 3: Calculate the Electric Field due to the Second Dipole
For the second dipole at (1m, 0, 2m):
- The distance r2 from (1, 0, 2) to (1, 0, 0) is 2m.
- Therefore, the electric field →E2 at (1, 0, 0) is:
→E2=14πϵ0⋅2⋅P2^k(2)3=14πϵ0⋅P^k8=P32πϵ0^k
Step 4: Determine the Direction of Each Electric Field
- The electric field →E1 from the first dipole points in the positive ^k direction.
- The electric field →E2 from the second dipole also points in the positive ^k direction.
Step 5: Calculate the Resultant Electric Field
The resultant electric field →Enet at point (1, 0, 0) is the vector sum of →E1 and →E2:
→Enet=→E1+→E2=(P2πϵ0+P32πϵ0)^k
To combine these, we need a common denominator:
→Enet=(16P32πϵ0+P32πϵ0)^k=17P32πϵ0^k
Final Result
The resultant electric field at the point (1m, 0, 0) due to the two dipoles is:
→Enet=17P32πϵ0^k
- The first dipole, →p1=P^k, is located at the origin (0, 0, 0).
- The second dipole, →p2=P2^k, is located at (1m, 0, 2m).
The electric field →E1 due to a dipole at a point in space is given by the formula:
→E=14πϵ0⋅2→pr3
where →p is the dipole moment and r is the distance from the dipole to the point of interest.
- The distance r1 from (0, 0, 0) to (1, 0, 0) is 1m.
- Therefore, the electric field →E1 at (1, 0, 0) is:
→E1=14πϵ0⋅2P^k(1)3=2P4πϵ0^k=P2πϵ0^k
For the second dipole at (1m, 0, 2m):
- The distance r2 from (1, 0, 2) to (1, 0, 0) is 2m.
- Therefore, the electric field →E2 at (1, 0, 0) is:
→E2=14πϵ0⋅2⋅P2^k(2)3=14πϵ0⋅P^k8=P32πϵ0^k
- The electric field →E1 from the first dipole points in the positive ^k direction.
- The electric field →E2 from the second dipole also points in the positive ^k direction.
The resultant electric field →Enet at point (1, 0, 0) is the vector sum of →E1 and →E2:
→Enet=→E1+→E2=(P2πϵ0+P32πϵ0)^k
To combine these, we need a common denominator:
→Enet=(16P32πϵ0+P32πϵ0)^k=17P32πϵ0^k
The resultant electric field at the point (1m, 0, 0) due to the two dipoles is:
→Enet=17P32πϵ0^k
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Multiple Correct Answer Type
1 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
Similar Questions
Two point charges −q and +q are located at points (0,0−a) and (0,0,a) respectively. The electric potential at point (0,0,z)is (Z>a)
View SolutionA dipole of dipole moment →P=2ˆi−3ˆj+4ˆk is placed at point A (2, -3, 1). The electric potential due to this dipole at the point B (4, -1, 0) is equal to (All the parameters specified here are in S.L. units) ____×109 volts
View SolutionA dipole of dipole moment →P=2ˆi−3ˆj+4ˆk is placed at point A (2, -3, 1). The electric potential due to this dipole at the point B (4, -1, 0) is equal to (All the parameters specified here are in S.L. units) ____×109 volts
View SolutionA electric dipole of dipole moment →p=9ˆi+3ˆj-3ˆk is placed at the point M(2 -3 1) .If the electric potential due to this dipole at the point N(4, -1, 0) is N times109 volt.Then find N if the given data is in S.l units
View SolutionThree point charge q1=1μC,q2=−2μC and q3=3μC are placed at (1m,0,0),(0,2m,0) and (0,0,3m) respectively. Find the electric potential at as origin.
View SolutionTwo small electric dipoles each of dipole moment pˆi are situated at (0,0,0) and (r,0,0). The electric potential at a point (r2,√3r2,0) is:
View SolutionTwo particles A and B are placed in gravity free space at (0,0,0)mand(30,0,0)m respectively. Particle A is projected with a velocity (5ˆi+10ˆj+5ˆk)ms−1, while particle B is projected with a velocity (10ˆi+5ˆj+5ˆk)ms−1 simultaneously. Then,
View SolutionTwo straight lines having variable slopes m1andm2 pass through the fixed points (a,0)and(−a,0) respectively. If m1m2=2, then the eccentricity of the locus of the point of intersection of the lines is
View Solutiontwo point charges 2μC and −4μC are situated at points (−2m,0m) and (2m,0m) respectively. Find out potential at point C(4m,0m) and D(0m,√5m).
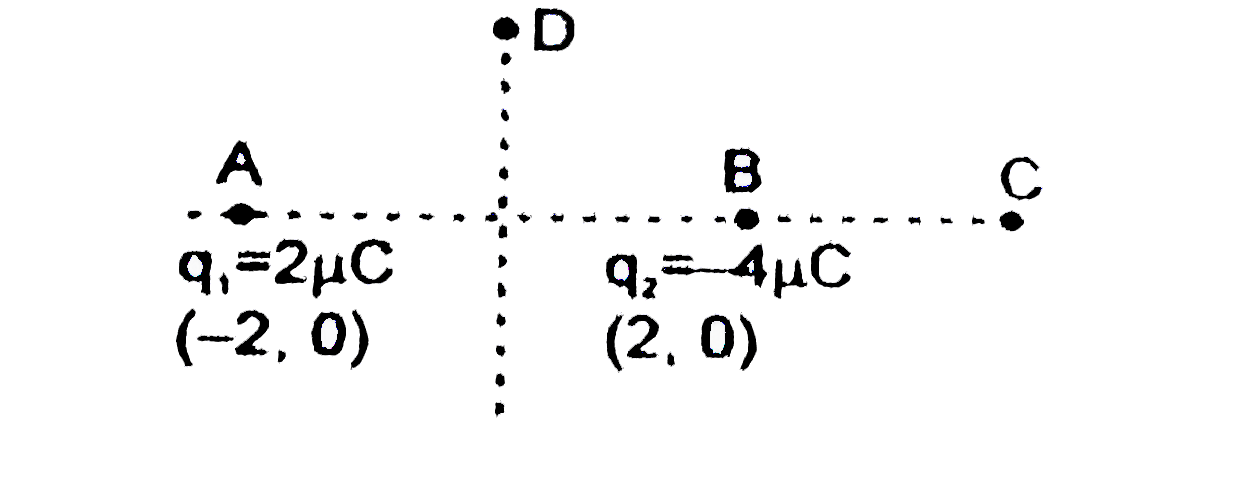
View Solutiontwo point charges + 16 q and -4q located at x=0 and x=L respectively. the location of a point on the x-axis from x=0, at which the net electric field due to these two charges is zero is
View Solution
