State and prove parallel axes theorem
Text Solution
Parallel axes theorem : The moment of inertia of a rigid body about any axis parallel to the axis passing through centre of mass is the sum of moment of inertia about the axis passing through centre of mass (lG) and mass of the body multiplied by square of distance (MR2) between the axes. i.e., l=lG+MR2
Proof: Consider a rigid body of mass M with .G. as its centre of mass. Let the moment of inertia about the axis passing through . centre of mass is lG Choose another parallel axis passing through the point .O. in that plane.
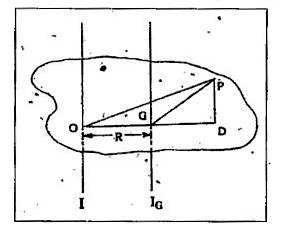
Let perpendicular distance between the axesis OG=R(say) Choose any point P in the given plane. Join OP and GP. Extend the line OG and drop a normal from .P. on to it. This is as shown in figure
The moment of inertia about the axis passing through centre of mass G is saylG=∑mGP2 ... (1)
M.O.I. of the body about the new axis passing through .O. is l=∑mOP2 . . .(2)
But from triangle OPD
OP2=OD2+DP2
But OD=OG+GD
∴OD2=(OG+GD)2=OG2+2OG.GD . . . (3)
From Equation (2) and (3)
l=∑mOP2=∑m[OG2+GD2+2OG.GD)+DP2]
∴l=∑m{GD2+DP2+OG2+2OG.GN}
But GD2+DP2=GP2
∴l=∑m{GP2+OG2+2OG.GD}
∴l=∑mGP2+∑mOG2+2OG∑mGD . . . (4)
But the terms ∑mGP2=lG (M.O.l. about centre of mass )
∑mOG2=MR2(∴∑m=MandOG=R)
The term 2 OG ∑mGD=0 . Because it represent sum of moment of masses about centre of mass. Hence its value is zero
∴l=lG+MR2
Hence parallel axis theorem is proved
|
Topper's Solved these Questions
- MODEL PAPER 11BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MODEL PAPER 11EXERCISE - Section - C
3 Videos
- MODEL PAPER 11BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MODEL PAPER 11EXERCISE - Section - C
3 Videos
- MODEL PAPER 10BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MODEL PAPER 10EXERCISE - Section - C
3 Videos
- MODEL PAPER 12BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MODEL PAPER 12EXERCISE - SECTION - C
3 Videos
Similar Questions
State (i) parallel axes theorem and (ii) perpendicular axes theorem.
View SolutionState and prove Bernoulli's theorem.
View SolutionState and prove the Pythagoras theorem.
View SolutionState and prove the Pythagoras theorem.
View SolutionState and prove theorem of parallel axes.
View SolutionState and prove theorem of parallel axes.
View SolutionState theorem of parallel axes.
View SolutionState and prove Bernouli's theorem.
View SolutionState and prove Gauss's law in electrostatics.
View SolutionState and prove theorem of perpendicular axes.
View Solution
